为什么前序和中序或者中序和后序，两两组合能构建一个二叉树？
因为前序和后序可以确定根，而中序可以划分出左右区间。

从前序与中序遍历序列构造二叉树

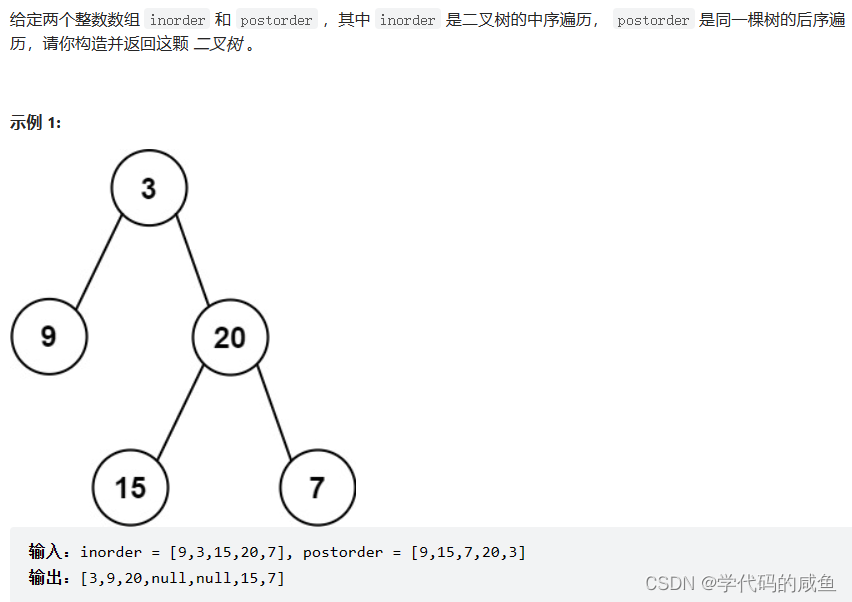
难度 中等 题目链接

思路讲解：
首先，根据前序我们可以确定根为3，然后在中序中我们可以根据3来划分左右区间。也就是[begin，rooti-1]rooti[rooti+1，end]。所以一开始的区间是[0，0]1[2，4]。

然后根据根，左子树，右子树来构造，所以下面我们要先构造左子树。preorder来到了9的位置，所以9是左子树的根。然后要从中序划分9的左子树和右子树的区间[0，-1]0[1，0]。

很显然，9没有左子树区间和右子树区间，就返回空。3的左子树就完成了，链接起来。然后preorder继续往下走来到了20的位置。那么20就是右子树的根。然后要从中序划分20的左子树和右子树的区间。

20的左子树和右子树的区间为[2，2]3[4，4]。然后再根，左子树，右子树。所以先构造20的左子树。

那么15的左子树区间和右子树区间都不存在，所以返回空。那么20的左子树构建完成，链接起来。然后构造20的右子树。

那么此时3的右子树已完成了，我们就会链接起来。这样一颗二叉树就构建完成了。

代码实现：
既然我们要遍历preorder，那么我们要定义一个变量来走。inorder需要划分左右空间，则需要两个变量。

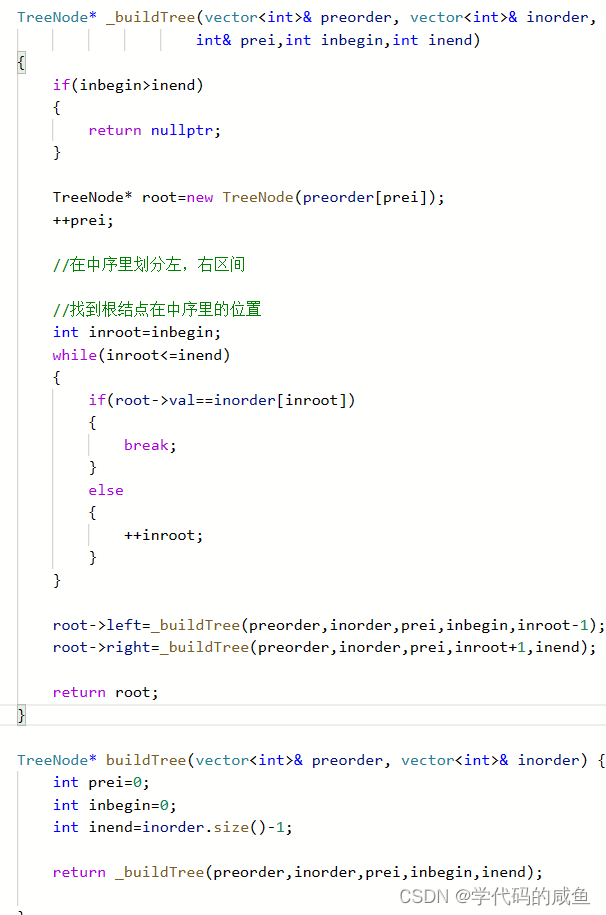
这里要主要prei需要加引用，因为递归回来时下标要发生变化。

从中序与后序遍历序列构造二叉树

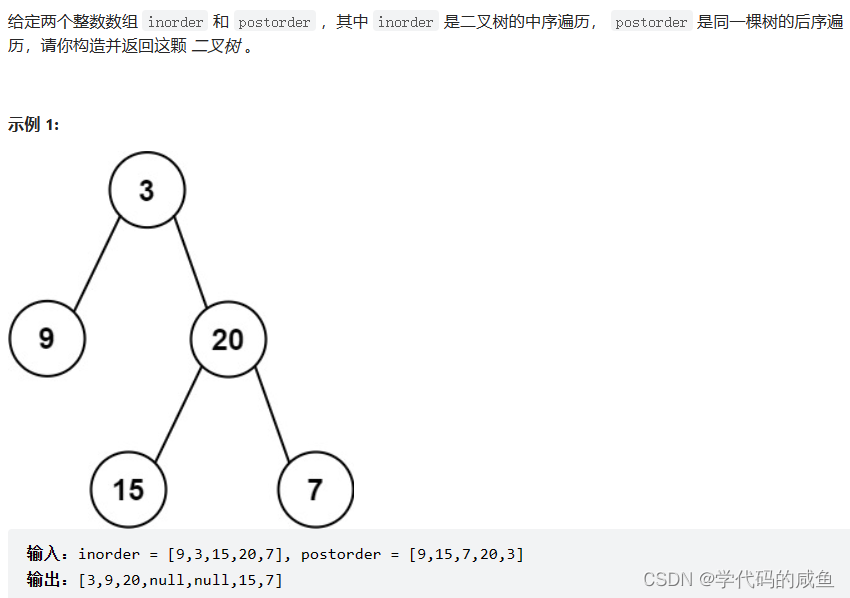
难度 中等 题目链接
这道题和上一题的大致思路是一样的。区别是：后序遍历我们要从后往前找根。然后后续遍历是左子树，右子树，根。所以先构造的是右子树了，其它的都一样。

代码如下：