目录
一.大数定理
二.监督学习方法
1.初始概率
2.转移概率
3.观测概率
三.Baum-Welch算法
1.EM算法整体框架
2. Baum-Welch算法
3.EM过程
4.极大化
5.初始状态概率
6.转移概率和观测概率
四.预测算法
1.预测的近似算法
2.Viterbi算法
1.定义
2. 递推:
3. 终止:
五.总结
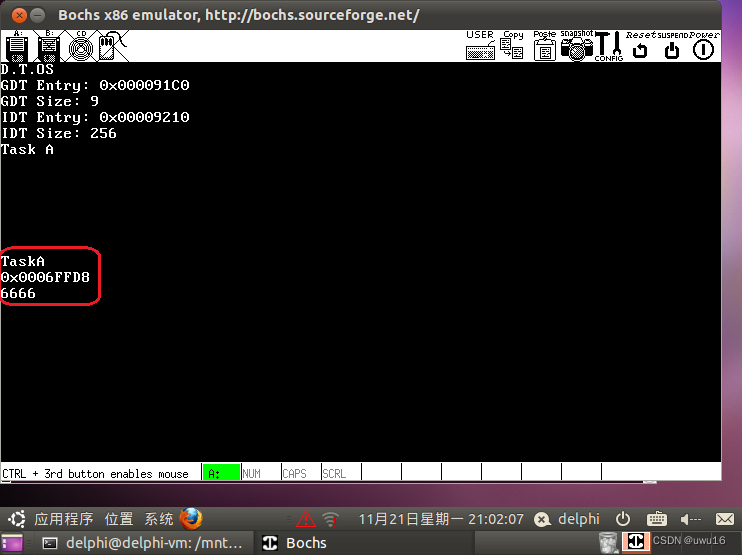
一.大数定理
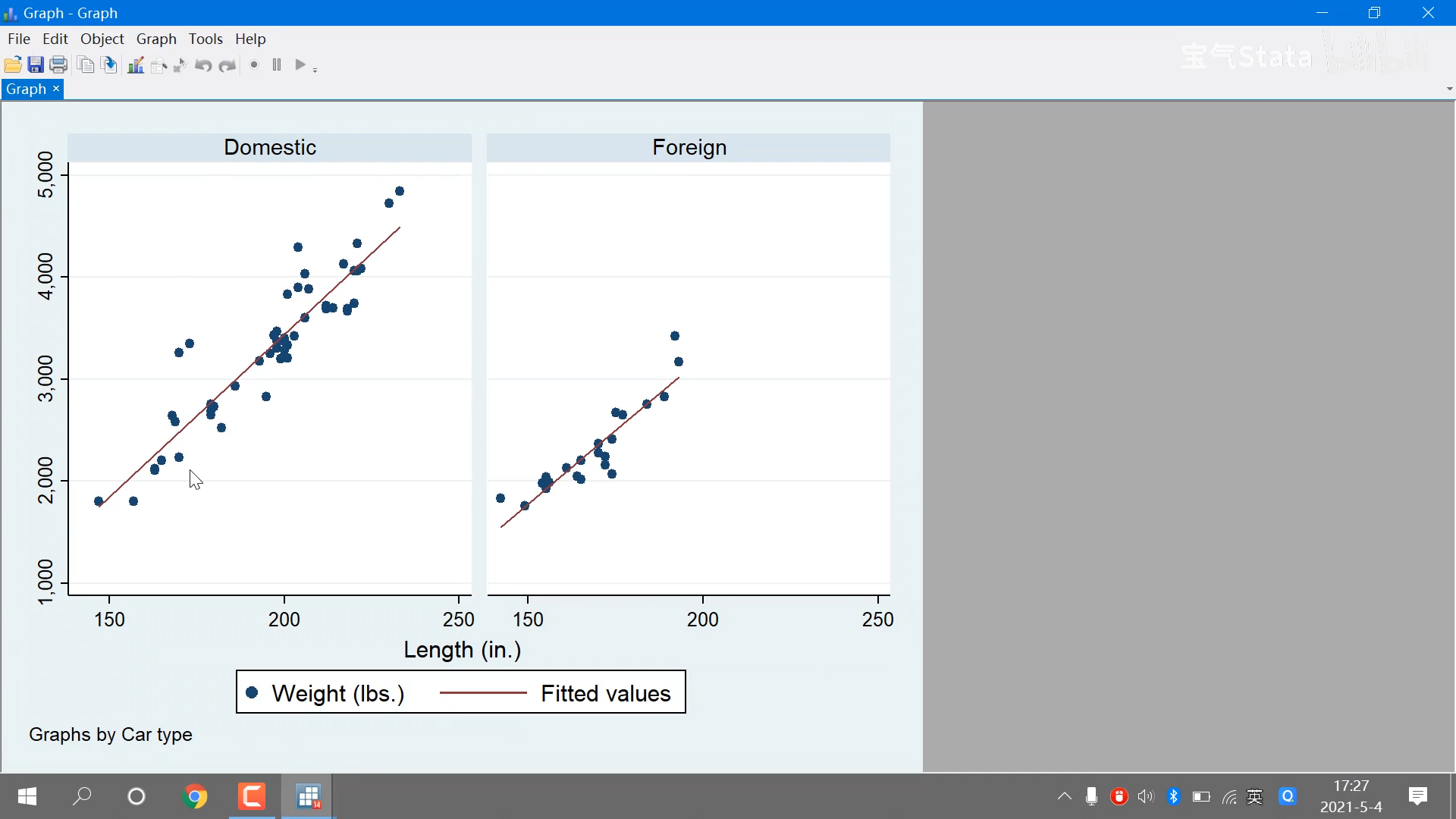
假设已给定训练数据包含S个长度相同的观测序列和对应的状态序列{(O1,I1),(O2,I2)…(Os,Is)},那么,可以直接利用Bernoulli大数定理的结论“频率的极限是概率”,给出HMM的参数估计。
二.监督学习方法
1.初始概率
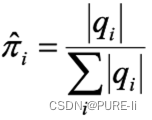
2.转移概率
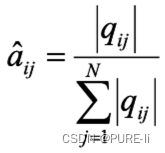
3.观测概率

三.Baum-Welch算法
若训练数据只有观测序列,则HMM的学习需要使用EM算法,是非监督学习。
1.EM算法整体框架
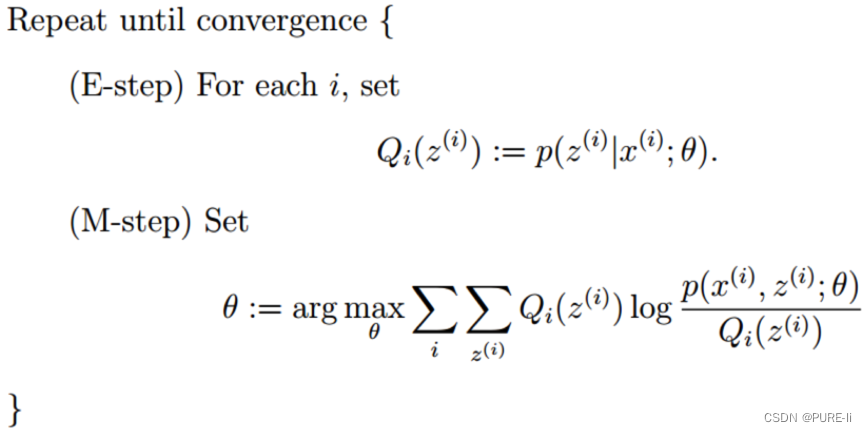
2. Baum-Welch算法
所有观测数据写成O=(o1,o2…oT),所有隐数据写成I=(i1,i2…iT),完全数据是(O,I)=(o1,o2…oT,i1,i2…iT),完全数据的对数似然函数是lnP(O,I|λ)
假设 是HMM参数的当前估计值,λ为待求的参数。
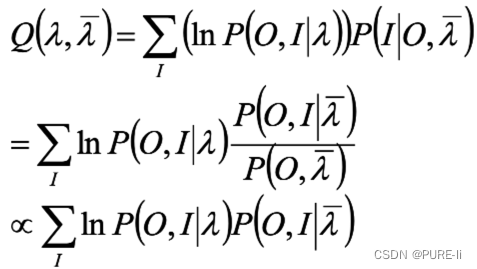
3.EM过程
根据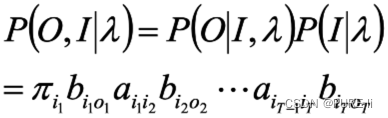
函数可写成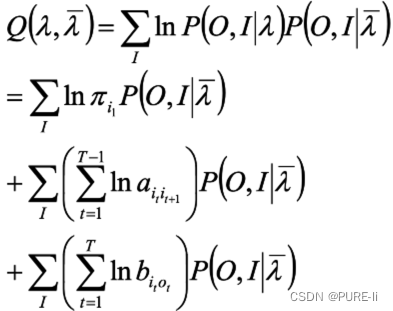
4.极大化
极大化Q,求得参数A,B,π
由于该三个参数分别位于三个项中,可分别极大化
![]()
注意到πi满足加和为1,利用拉格朗日乘子法,得到:
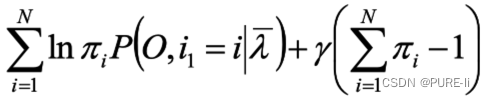
5.初始状态概率
对上式相对于πi求偏导,得到:
![]()
对i求和,得到:
![]()
从而得到初始状态概率:
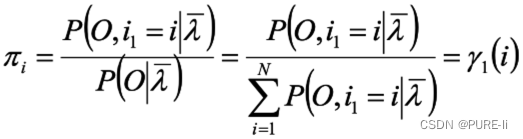
6.转移概率和观测概率
第二项可写成:
![]()
仍然使用拉格朗日乘子法,得到
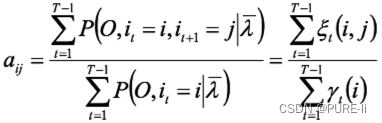
同理,得到:
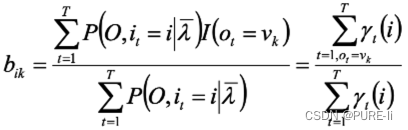
四.预测算法
1.预测的近似算法
在每个时刻t选择在该时刻最有可能出现的状态it*,从而得到一个状态序列I*={i1*,i2*…iT*},将它作为预测的结果。
给定模型和观测序列,时刻t处于状态qi的概率为:
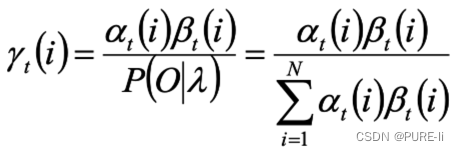
选择概率最大的i作为最有可能的状态
会出现此状态在实际中可能不会发生的情况
算法:走棋盘/格子取数
给定m*n的矩阵,每个位置是一个非负整数,从左上角开始,每次只能朝右和下走,走到
右下角,求总和最小的路径。

走的方向决定了同一个格子不会经过两次。
若当前位于(x,y)处,它来自于哪些格子呢?
dp[0,0]=a[0,0] / 第一行(列)累积
dp[x,y] = min(dp[x-1,y]+a[x,y],dp[x,y-1]+a[x,y])
即:dp[x,y] = min(dp[x-1,y],dp[x,y-1]) +a[x,y]
2.Viterbi算法
Viterbi算法实际是用动态规划解HMM预测问题,用DP求概率最大的路径(最优路径),这是一条路径对应一个状态序列。
定义变量δt(i):在时刻t状态为i的所有路径中,概率的最大值。
1.定义
![]()
2. 递推:
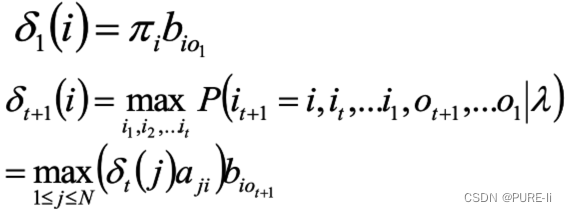
3. 终止:
![]()
五.总结
马尔科夫模型可以用来统一解释贪心法和动态规划。
HMM解决标注问题,在语音识别、NLP、生物信息、模式识别等领域被广泛使用。
定义变量δt(i):在时刻t状态为i的所有路径中,概率的最大值。
加强算法模型和实践问题的相互转换能力。