1.重建二叉树
class Solution {
public:
TreeNode* traversal(vector<int>& preorder,vector<int>& inorder){
if(preorder.size()==0) return NULL;
int rootValue=preorder.front();
TreeNode* root=new TreeNode(rootValue);
//int rootValue=preorder[0];
if(preorder.size()==1) return root;
int index;
for(index=0;index<inorder.size();index++)
{
if(inorder[index]==rootValue)
break;
}
//中序的左右数组
vector<int> inorderleft(inorder.begin(),inorder.begin()+index);
vector<int> inorderright(inorder.begin()+index+1,inorder.end());
//前序的左右数组
vector<int> preorderleft(preorder.begin()+1,preorder.begin()+1+inorderleft.size());
vector<int> preorderright(preorder.begin()+1+inorderleft.size(),preorder.end());
root->left=traversal(preorderleft,inorderleft);
root->right=traversal(preorderright,inorderright);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if(preorder.size()==0||inorder.size()==0) return NULL;
return traversal(preorder,inorder);
}
};2.数值的整数次方
首先解决超级次方这个题目,这个题目有三个问题需要解决:
b是一个数组,应该如何处理?
如何处理求模的结果?
如何高效的进行幂运算?
<1> 如下图所示,每次都可以将数组中的最后一个元素提出来,于是这里面隐藏了一个递归的过程;

<2>每次遇到乘法时,都得防止发生溢出,利用如下公式,对每次a与乘出的结果都做一次取模运算;
(a * b) % k = (a % k) * (b % k) % k
<3>如下图所示,在幂运算过程中仍然可以递归,这样可以实现O(logn)的时间复杂度;
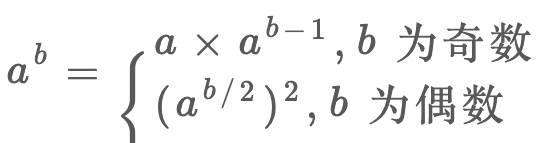
#define base 1337
class Solution {
public:
//1.幂运算常规做法
//每次做乘法时都得防止溢出
//(a*b)%k=(a%k)*(b%k)%k
/*
int myPow(int a,int b){
a%=base;
int res=1;
for(int i=b;i>0;i++)
{
res*=a;
res%=base;
}
return res;
}
*/
//2.高效幂运算
int myPow(int a,int b){
if(b==0) return 1;
a%=base;
if(b%2==1) //如果b是奇数
return (a*myPow(a,b-1))%base;
else //如果b是偶数
{
int sub=myPow(a,b/2);
return (sub*sub)%base;
}
}
int superPow(int a, vector<int>& b) {
if(b.empty()) return 1;//b为空
int last=b.back();//将b的最后一个元素提出来
b.pop_back();
int part1=myPow(a,last);
int part2=myPow(superPow(a,b),10);
return (part1*part2)%base;
}
};接下来是对本题进行讨论:
需要注意的是n的取值范围,可以发现当n为最小值时,直接取反会导致整型溢出,于是需要将这种情况单独进行讨论。

class Solution {
public:
double myPow(double x, int n) {
if(n==0) return 1;
//比较恶心的是注意一下n的范围,如果n为负的最小值,-2的31次方时,直接取负数会导致整型溢出
if(n==INT_MIN) return myPow(1/x,-(n+1))/x;
//接下来再正常讨论,n为负、正时的情况
if(n<0) return myPow(1/x,-n);
//n为奇数时
if(n%2==1) return x*myPow(x,n-1);
else
{
double sub=myPow(x,n/2);
return sub*sub;
}
}
};3.二叉搜索树的后序遍历
后序遍历 左右中,那么数组整体应该为左孩子-右孩子-根结点。
归根结底仍是数组与二叉树之间的转换问题,那么就离不开寻找切割点;
找到切割点后,右子树的所有点应该比根结点的值才对,否则返回false。
class Solution {
public:
bool check(vector<int>& postorder,int left,int right){
//终止条件
if(left>=right) return true;//空节点或者只有一个节点的时候
int rootValue=postorder[right];//根结点的值
//接下来还是分割数组,左孩子都比根结点小,右孩子都比根结点大
int point=left;//分割点
while(point<right&&postorder[point]<rootValue){
point++;
}
//在point开始到right之间的所有值都应该比rootValue大
int i=point;
while(i<right&&postorder[i]>rootValue) {
i++;
}
if(i!=right) return false;
bool leftBool=check(postorder,left,point-1);
bool rightBool=check(postorder,point,right-1);
return leftBool&&rightBool;
}
bool verifyPostorder(vector<int>& postorder) {
return check(postorder,0,postorder.size()-1);
}
};