本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。
文章目录
- 信源编码
- 分类
- 前缀条件
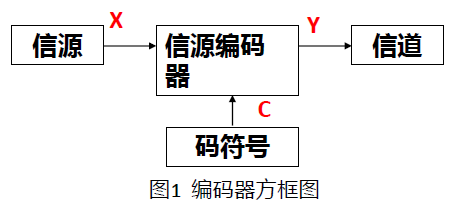
码符号C表示的是编码的字符集。如二进制编码,c:{0,1} (无特殊说明,本章所有编码都是二进制编码);
信源编码就是将信源符号序列按照一定的数学规律映射成由码符号组成的码序列的过程。
- 信源编码器输入的消息序列:
X = ( X 1 X 2 … X l … X L ) , X l ∈ { a 1 , … a n } \boldsymbol{X}=(X_{1} X_{2} \ldots X_{l} \quad \ldots X_{L}) , X_{l} \in\{a_{1}, \ldots a_{n}\} X=(X1X2…Xl…XL),Xl∈{a1,…an}
输入的消息总共有 n L n^{L} nL 种可能的组合
-
输出的码字 (码序列) 为:
Y = ( Y 1 Y 2 … Y k … Y K ) , Y k ∈ { b 1 , … b m } \begin{array}{l} Y=(Y_{1} Y_{2} \ldots Y_{k} \ldots Y_{K}), Y_{k} \in\{b_{1}, \ldots b_{m}\} \end{array} Y=(Y1Y2…Yk…YK),Yk∈{b1,…bm}
输出的码字总共有 m K m^{K} mK种可能的组合。
信源编码
将信源输出符号X, 经信源编码器后变换成另外的压缩符号Y, 然后将压缩后信息经信道传送给信宿。
信源符号之间存在分布不均匀和相关性,使得信源存在冗余度,信源编码的主要任务就是减少冗余,提高编码效率。
针对信源输出符号序列的统计特性, 寻找一定的方法把信源输出符号序列变换为最短的码字序列。
分类
分组码和非分组码
1.分组码: 信源序列在进入编码器之前先分成若干信源符号组(也称信源字),将信源编码器根据一定的规则用码符号序列(也称码字)表示信源字作为编码器的输出。
2.非分组码: 信源序列连续不断地从编码器的输入端进入,同时在编码器的输出端连续不断的产生码序列。

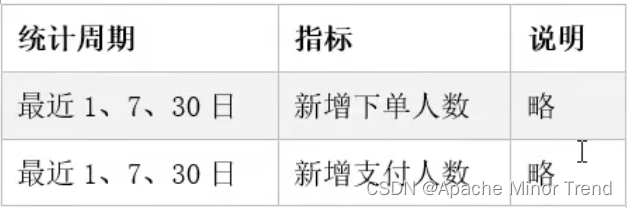
例 信源符号 X = { a 1 , a 2 , a 3 , a 4 } X=\{a_{1}, a_{2}, a_{3}, a_{4}\} X={a1,a2,a3,a4}对应不同码字如表
该信源的信息熵为:1.75 bit/symbol
等长码:码中所有码字的长度都相同,如:码0
变长码;码中的码字长短不一,如:码1、2、3、4
非奇异码:信源符号与码字是一一对应的,如:码0、2、3、4
奇异码:信源符号与码字不是一一对应的,如:码1
唯一可译码: 任意有限长的码元序列,只能被唯一地分割成一个个的码字。如码0、3、4。
例:{0,10,11}是一种唯一可译码。
任意一串有限长码序列,如100111000,只能被分割成 10,0,11,10,0,0。任何其他分割法都会产生一些非定义的码字。
奇异码不是唯一可译码
非奇异码
- 唯一可译码,如: 码3;
- 非唯一可译码,如:码2;
-
非即时码(延长码)
如果接收端收到一个完整的码字后不能立即译码,还需等下一个码字开始接收后才能判断是否可以译码,如:码 3;在延长码中有的码是唯一可译的取决于码的总体结构。 -
即时码 (非延长码 ) (异前缀码 )
在译码时无需参考后续的码符号就能立即 作出判断 译成对应的信源符号。如:码 0 、 4
任意一个码字都不是其它码字的 前缀 部分——前缀条件。
可以证明,一种可唯一译码并且具有即时性的编码方法必定满足前缀条件。
前缀条件
任意一个码字都不是其它码字的前缀部分----前缀条件。
如:码0: 00、01、10、11。码4: 1、01、001、0001
可以证明,一种可唯一译码并且具有即时性的编码方法必定满足前缀条件。
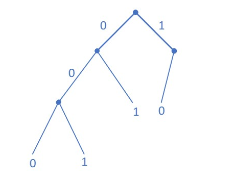
判断码:000、001、01、10是否唯一可译?是否是即时码?
由上图可知,都是。
参考文献:
- Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- 周炯槃. 通信原理(第3版)[M]. 北京:北京邮电大学出版社, 2008.
- 樊昌信, 曹丽娜. 通信原理(第7版) [M]. 北京:国防工业出版社, 2012.