感谢原作者!原文传送门
以下是摘录:
1、什么是辛普森悖论?
辛普森悖论是 1951 年由 E.H. 辛普森提出的,简单来讲就是在分组比较中都占优势的一方,有的时候在总评中反而是失势的一方。指局部的结论和整体的结论完全相反。
举个栗子:
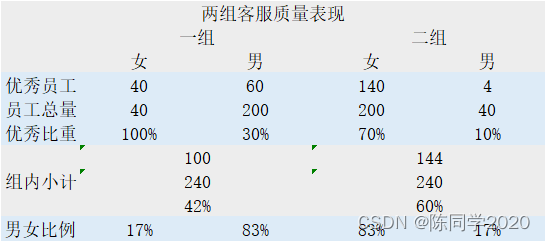
解读:女性员工表现,一组好于二组;男性员工表现,一组好于二组。然而,从总体上来说,一组差于二组。
2、为什么会出现辛普森悖论?
从以上例子可以看出,一组和二组的性别比重差异大,即分组样本不均衡。一组的主要成员男性的表现(30%)低于二组主要成员女性的表现(70%)。
我们通常会讲到“质量”这个词,而且是一起出现,但实际上,“质”与“量”是两个不同的方面,我们在考虑质的时候,一定要注意量的影响,我们如果把这两者揉成一个“质”,就会出现辛普森悖论。
延申:①从绩效考评角度看,由于样本不均衡,二组因有更多声音甜美温柔耐心的女员工而拥有性别优势;一组已经输在了起跑线,不是输给了能力,而是输在了性别劣势。②从统计学上来讲,一组和二组不具有可比性,当我们设计对照组和实验组的时候,要确保非控制变量(性别)是均衡的,统计归因(控制变量)才有效。
3、在工作中的指导意义
【栗子1】公司的一位数据分析同事的竞品分析报告里提到:“我们客户的平均客单价是 100元钱,竞争对手的只有 50 元,我们的客户比对方的高端多了。所以我们产品要走高端路线”这些结论可信吗?还真不一定。
【栗子2】某游戏公司做了款游戏,有 Android 和 iOS 版本。一个数据分析师看完用户的付费数据后,发现整体上 iOS 付费率比较高。他就直接告诉老板说,“我们 iOS的用户付费率要高于Android的用户付费率,我们应该集中资源开发iOS客户端!”这个结论可信么?还真不一定。
因为很有可能出现这样一种情况:Android最大的优势(男性用户)没有比过iOS最大的优势(女性用户),这是决定最终整体走向的关键。
4、总体与局部,我们信哪个?
只要细分的用户群体足够大,有统计学意义上的显著性,那一定是以细分结论为准,因为真理都是需要抽丝剥茧,藏在细节处。
但是如果细分的群体太小,比如上面的例子中,细分以后各组的用户数都很小,不具统计学意义,那细分的结论就不可信了。
所以还是那句话,无论是整体还是细分,在看“质”的同时,一定要兼顾“量”的影响,这是理解辛普森悖论最重要的一点。