HashMap：
HashMap是面试中经常被问到的一个内容，以下两个经常被问到的问题，
Question1：底层数据结构，1.7和1.8有何不同？
答：1.7数组＋链表，1.8数组＋(链表|红黑树)
Question2：为何要用红黑树，为何一上来不树化，树化阈值为何是8，何时会转化，何时会退化为链表？
答： 红黑树用来避免 Dos 攻击，防止链表超长时性能下降，树化应当是偶然情况
hash 表的查找，更新的时间复杂度是 0(1)，而红黑树的查找，更新的时间复杂度是 0(log2^n)，TreeNode 占用空间也比普通 Node 的大，如非必要，尽量还是使用链表
hash 值如果足够随机，则在 hash 表内按泊松分布，在负载因子 0.75 的情况下，长度超过 8 的链表出现概率是0.00000006，选择8就是为了让树化几率足够小
树化两个条件:链表长度超过树化值;数组容量>=64
退化情况1:在扩容时,如果拆分树后，树元素个数<=6,则会退化链表
退化情况2: remove树节点之前，若 root、root.left、root.right、root.left.left 有一个为 null，也会退化为链表
如果你都可以回答出来，那么恭喜你不要高兴得太早，这只是开始，回答完之后面试官会进行一连串的追问，如果都没有回答出来，也不要过于沮丧，相信看完这篇文章会收获很多！
如下所示，我们将元素a放入Hashmap中，需要经历计算hash值，再和capacity进行求模再计算出桶下标
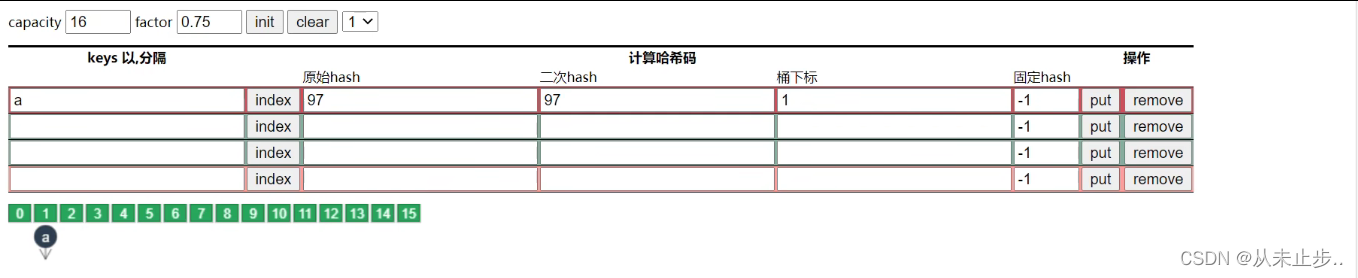经过上述一系列的操作，相信不少的小伙伴会产生疑惑，到底有没有必要为了存储一个元素而通过这么复杂的步骤呢？
当然有必要，这样做是为了后续快速查找元素！
如下所示：
对于下述数组，我们将其放入Hashtable中，如果我们想查找元素a，那么需要比较10次才能够找到该元素
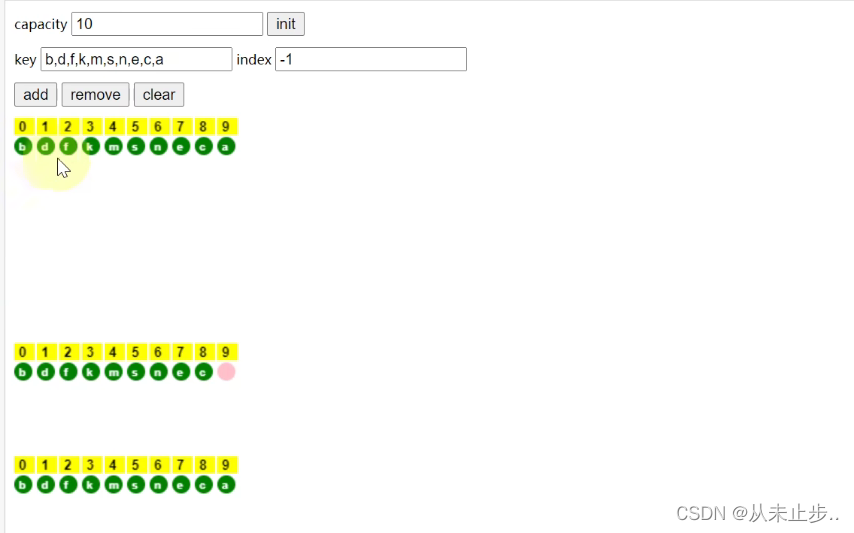
但如果将上述的数组的每个元素经过计算hash值，再和capacity进行求模再计算出桶下标，再放入HashMap中，如下所示：
此时我们如果想要查找元素a，那么可以直接通过计算桶下标进而确定元素a在下标为1的位置，这样我们只比较了一次。
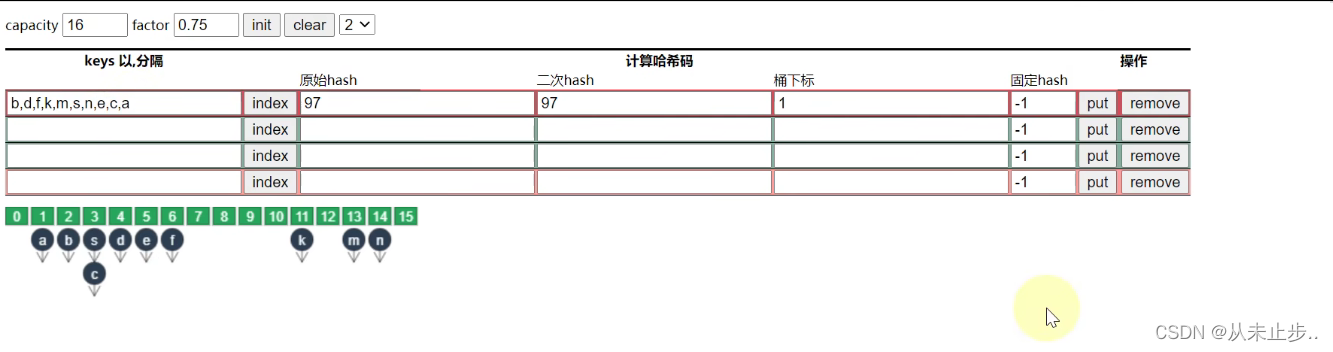
但上述这种是理想状态下，我们所查找的元素所处的下标只包含一个元素，此时的时间复杂度为O(1）
既然有最优情况，也就会有最极端的情况，如果当非常多的元素的桶下标计算出来都是相同的呢？
实例：
当我们想要查找元素8时，对于上述这种情况，即使计算出桶下标，但我们似乎还是需要比较8次，对此我们有两种解决思路-----------1：扩容，2：使用红黑树
使用扩容：
当元素的含量超过容器的3/4，就会进行扩容操作，如下所示：
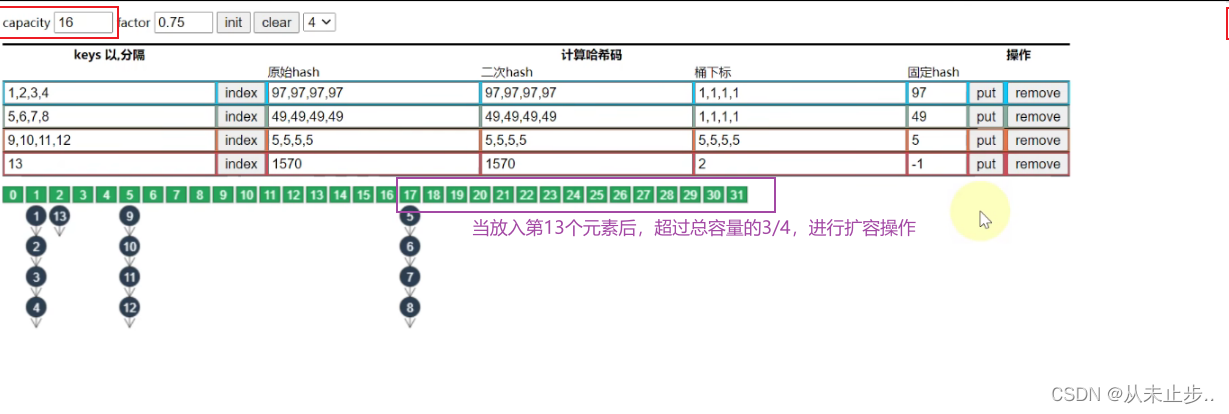
元素5,6,7,8的桶下标发生改变的原因为：此时的容量发生变化导致取模的结果也发方生变化，扩容后链表长度缩减
但扩容一定会导致链表长度的缩减吗？当然不是，当扩容后，没有元素桶下标的变化，自然就不会发生链表长度的缩减，如下所示：
对此，我们只有进行红黑树操作了
红黑树化：
当链表长度超过8并且总容量大于64，才会产生红黑树，而如果仅仅满足链表长度超过8时，会先通过扩容从而缩减链表长度，当扩容到64以后，才会红黑树化
举例：
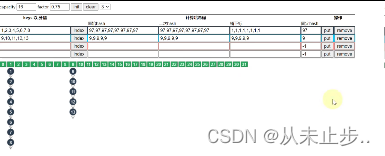
当我强制性的将a添加到桶下标为1的位置时，此时即使链表长度超过了8，但也不会生成红黑树，而是优先进行扩容操作，如下所示：
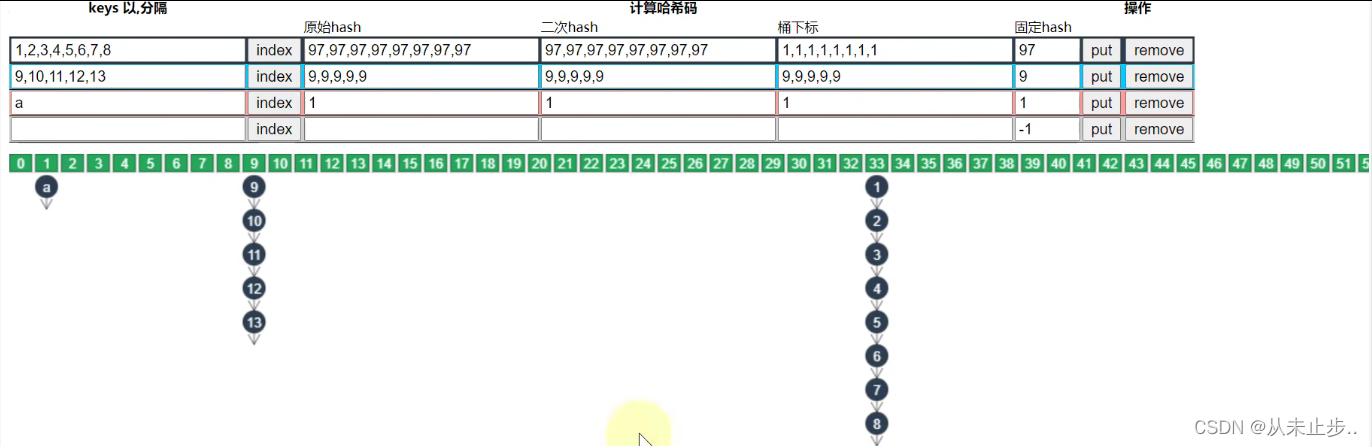
继续向桶下标为33的地方添加元素，此时总容量大于64已经满足，且添加过后，该链表长度也超过8，因此会发生红黑树化
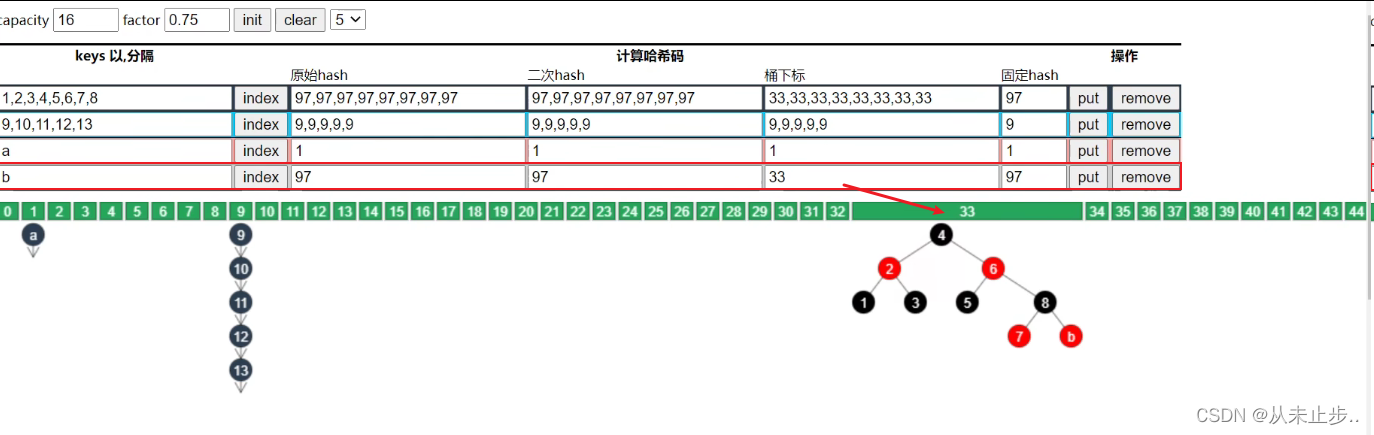
红黑树的特点：无论是根节点还是任意的子根节点都满足，(子)根节点左边的元素均小于(子)根节点，(子)根节点右边的元素均大于右(子)根节点
红黑树依然可以提高我们的查询效率，比如，此时我们需要查找元素8，那么只需要先确定元素8的桶下标，然后和4比较，再和6比较，最后和8比较，经过三次比较就可以找到元素8
链表的搜索时间复杂度为O(n),而红黑树的时间复杂度为O(log2^n)
注：某个桶下标的链表长度是可以超过8的，当总容量小于64时，并不会发生扩容，即使每次添加的桶下标为一个值，都不会红黑树化
索引的计算方法：
1：计算索引的hashCode()，再调用HashMap的hash()方法进行二次哈希，最后&(capacity-1)得到索引
2：二次hash()是为了综合高位数据，让哈希分布更为均匀
3：计算索引时，如果是2的n次幂可以使位与运算代替取模，效率更高，扩容时hash&oldCap==0的元素留在原来的位置，否则新位置=旧位置+oldCap
但1,2,3,都是为了配合容量为2的n次幂时的优化手段，例如：Hashtable的容量就不是2的n次幂，并不能说哪种设计更优，应该是设计者综合了各种因素，最终选择了使用2的n次幂作为容量
HashMap_put:
put方法流程，1.7和1.8有何不同？
1：HashMap是懒惰创建数组的，首次使用才创建数组
2：计算索引(桶下标)
3：如果桶下标还没人占用，创建Node占位返回
4:如果桶下标已经有人占用
1：已经是TreeNode走红黑树的添加或更新逻辑
2：是普通Node,走链表的添加或更新逻辑，如果链表长度超过树化阈值，走树化逻辑
5：返回前检查容量是否超过阈值，一旦超过则进行扩容
1.7 and1.8 的不同点:
链表插入节点时，1.7是头插法，1.8是尾插法
1.7是大于等于阈值且没有空位时才扩容，而1.8是大于阈值就扩容
1.8在扩容计算Node索引时，会优化---将哈希值与原来的哈希值进行按位与再判断
加载因子为何默认为0.75f？
在空间占用与查询时间之间取得较好的权衡
大于这个值，空间节省了，但链表就会比较长影响性能
小于这个值，冲突减少了，但扩容就会更频繁，空间占用多
多线程下会引发什么问题？
1.7：扩容死链
1.7和1.8数据错乱
扩容死锁的引发过程：
单线程下扩容的过程：
准备工作：
第一轮循环：
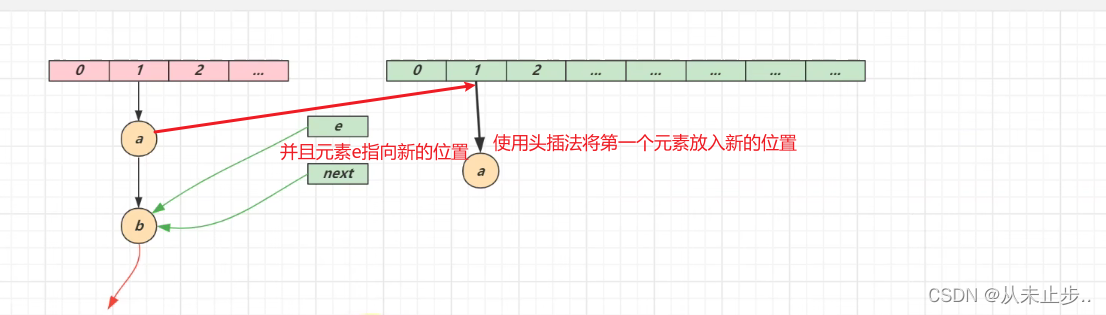
第二轮循环：
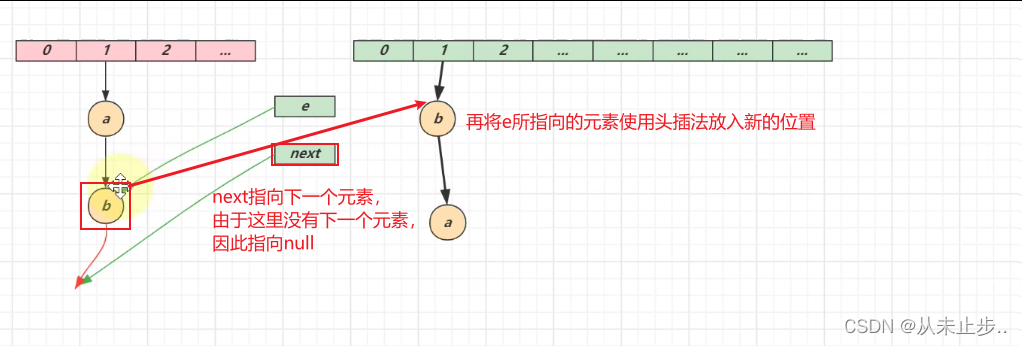
第二次循环结束，e指向下一个元素，进行第三次循环：
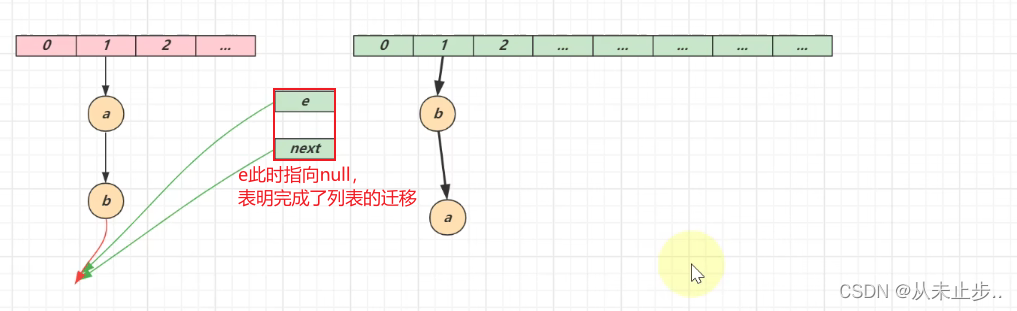
对象实现迁移并没有使得对象发生变化，只是对象的引用地址发生了变化，由于是头插法，因此使得迁移后的对象顺序发生了颠倒
多线程下扩容的过程：
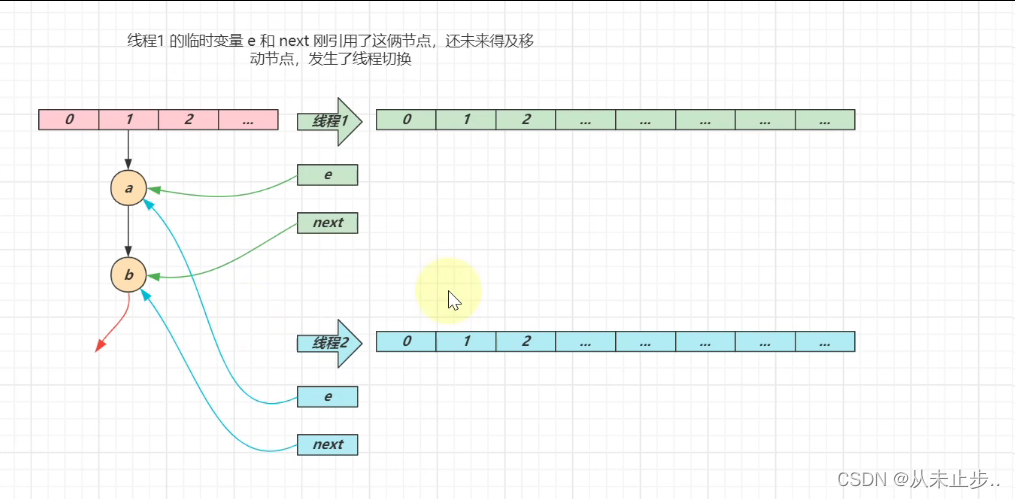
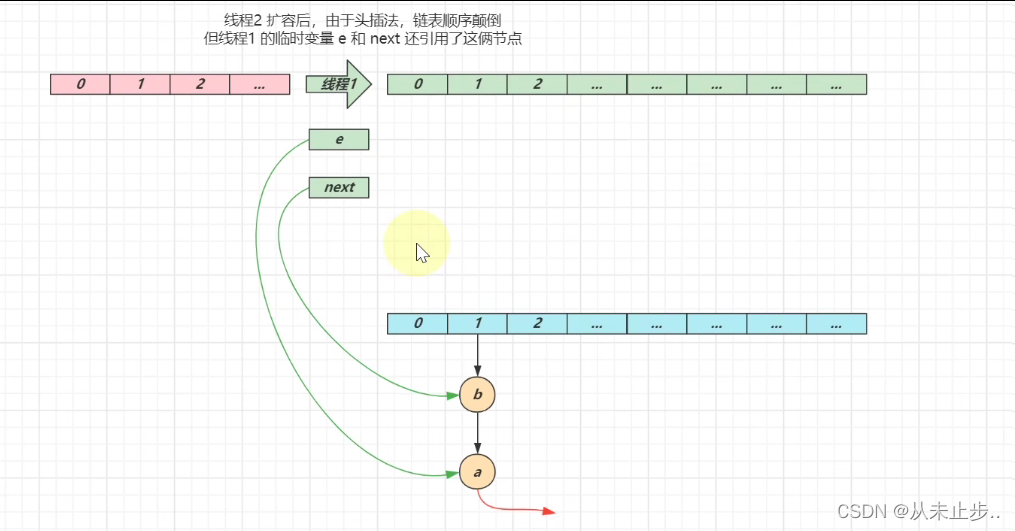
第一轮循环：
第一轮循环结束：
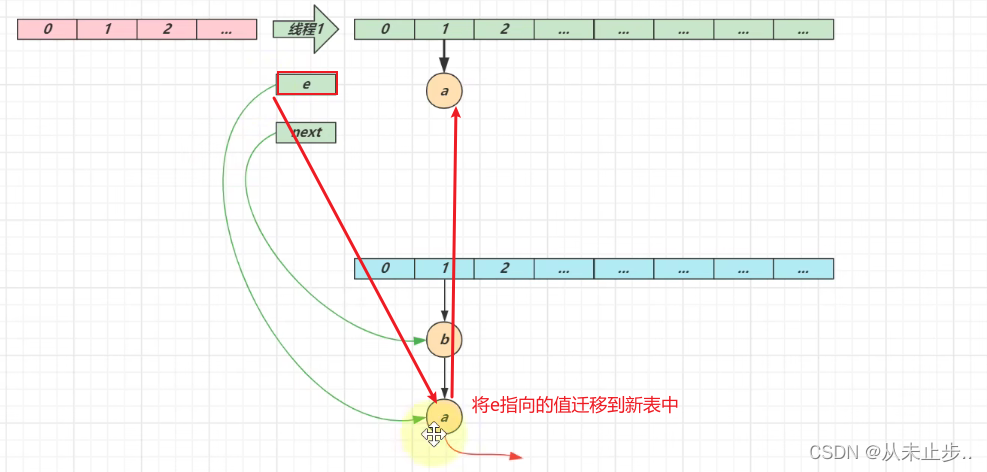
第二轮循环：
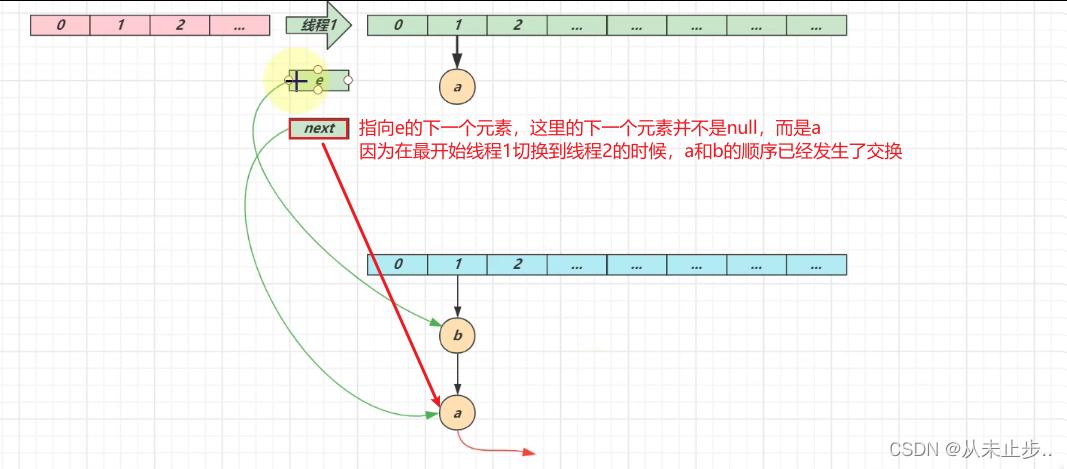
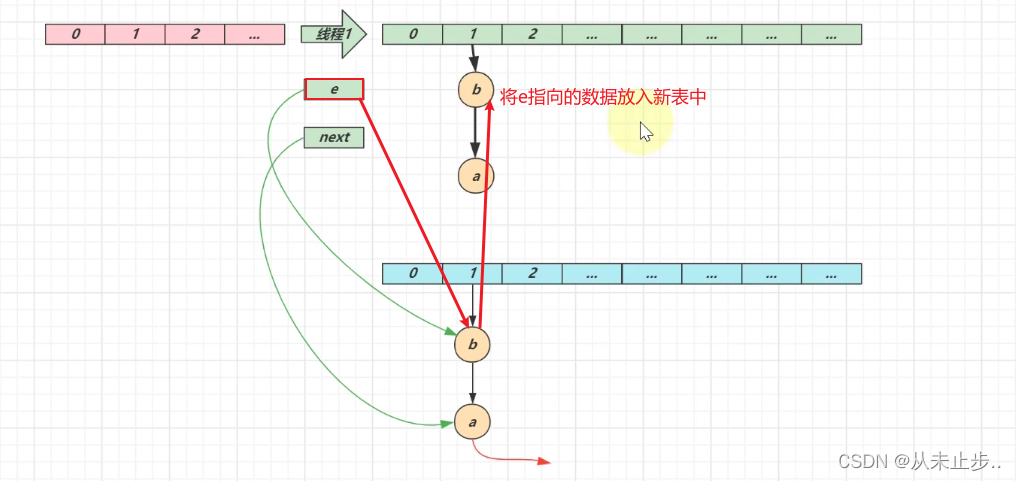
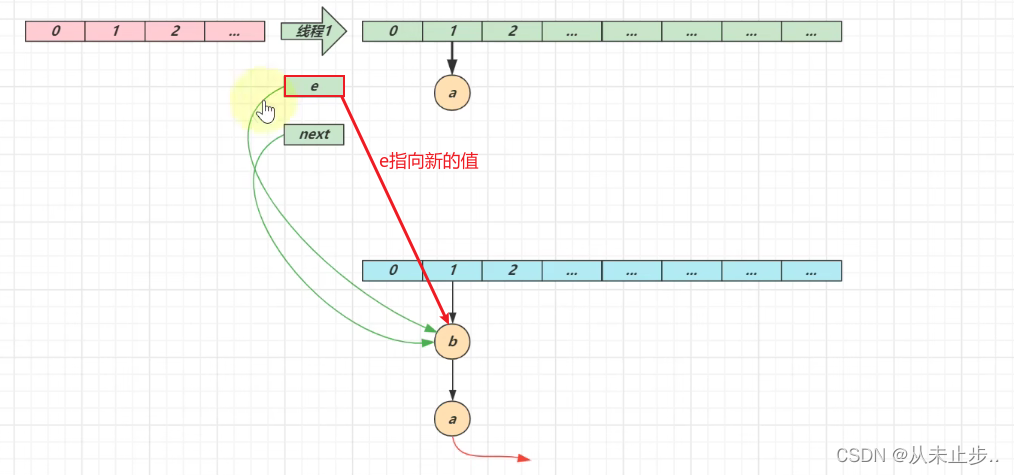
第二轮循环结束：
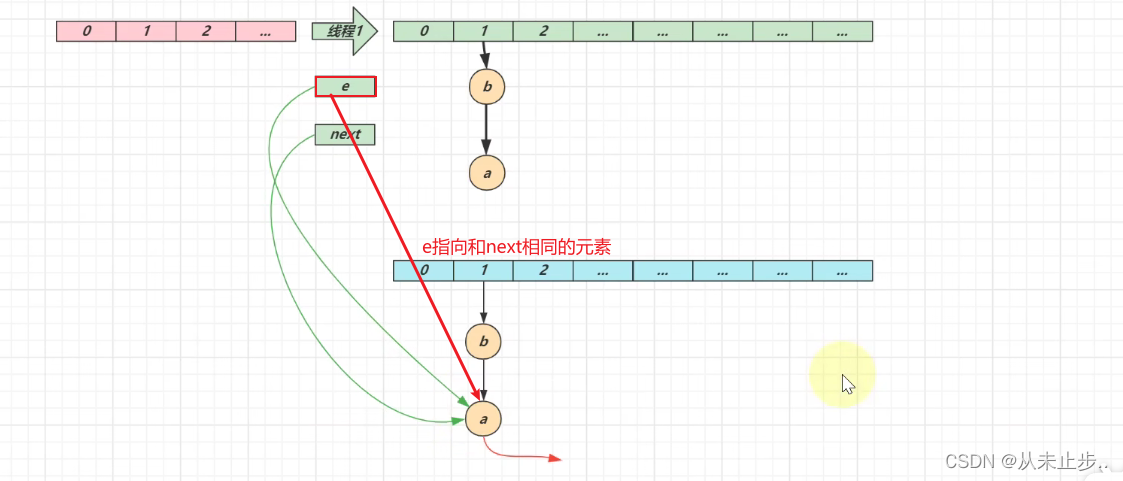
第三轮循环开始：
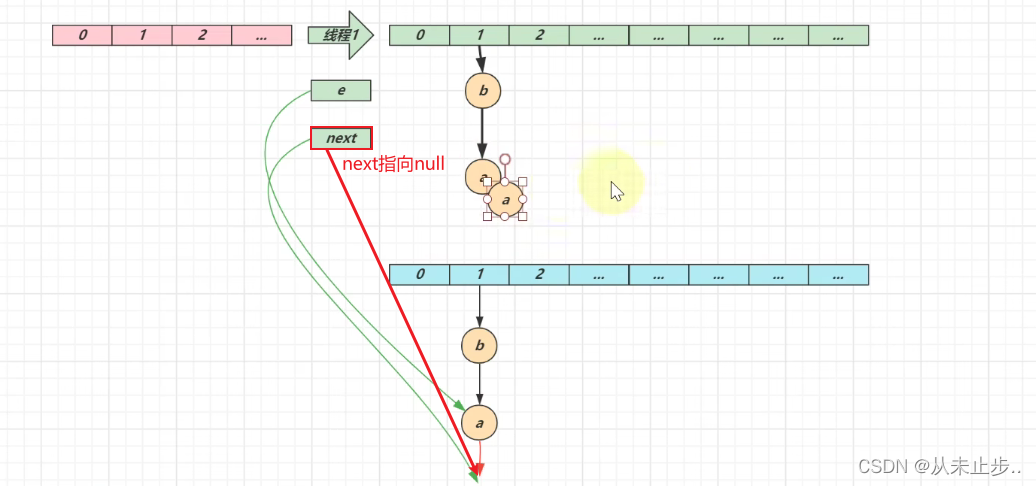
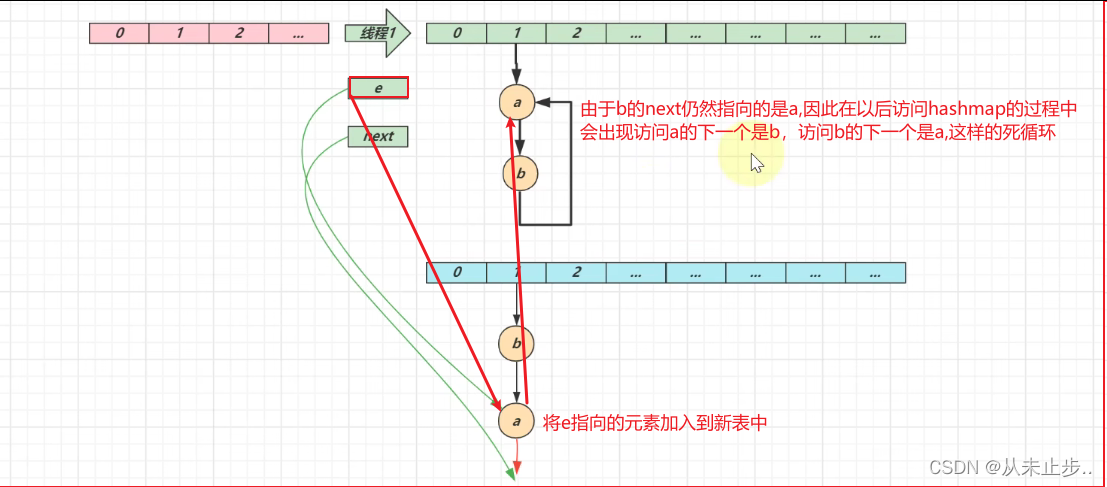
第三轮循环结束：
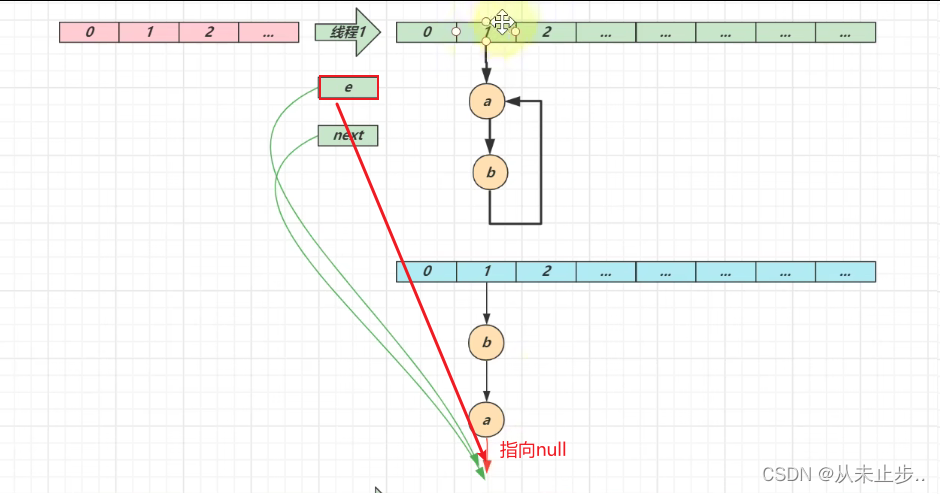
key能否为null，作为key的对象有什么要求？
HashMap的key可以作为null，但Map的其他实现则不然，比如treemap，作为key的对象，必须实现hashCode和equals,并且key的内容不能修改
不能修改的原因：
HashMap用Key的哈希值来存储和查找键值对，当插入一个Entry时，HashMap会计算Entry Key的哈希值，Map会根据这个哈希值把Entry插入到相应的位置，查找时，HashMap通过计算Key的哈希值到特定位置查找这个Entry，如果HashMap Key的哈希值在存储键值对后发生改变，Map可能再也查找不到这个Entry了，如果Key对象是可变的，那么Key的哈希值就可能改变，在HashMap中可变对象作为Key，会造成数据丢失，如果可变对象在HashMap中被用作键，那就要小心在改变对象状态的时候，不要改变它的哈希值了
必须实现hashCode和equals的原因：
如果只重写hashcode()不重写equals()方法，当比较equals()时，其实调用的是Object中的方法，只是看他们是否为同一对象（即进行内存地址的比较)
如果只重写equals()不重写hashcode()方法，在判断的时候，会被拦下HashMap认为是不同的Key，以对象作为HashMap的key，必须重写该对象的hashCode和equals方法，确保hashCode相等的时候equals的值也是true
String对象的hashCode()如何设计的，为什么每次乘的是31？
目的是达到较为均匀的散列效果，每个字符串的hashCode足够独特
字符串中的每个字符都可以表现为一个数字，称为Si,其中i的范围是0-n-1
散列公式为：S0*31^ n-1+S1*31^ n-2......Si*31^ n-1-i+..........Sn-1*31^0
31带入公式有较好的散列特性，并且31*h可以被优化为：
1：即32*h-h
2:即2^5*h-h
3:即h<<5-h
举例：
公式套入31的散列效果如下：
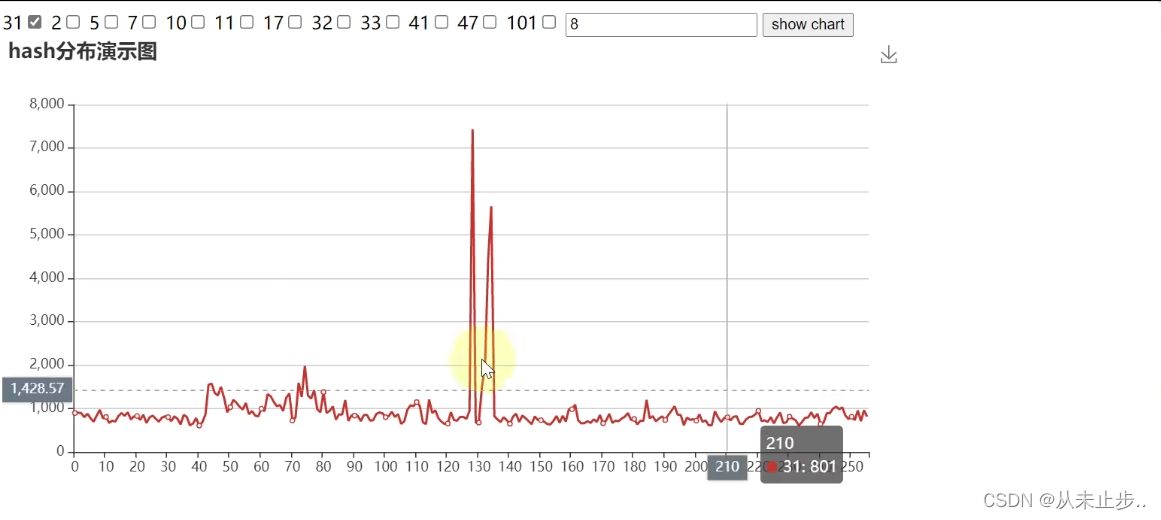
蓝色线条为公式套入2的散列效果如下：
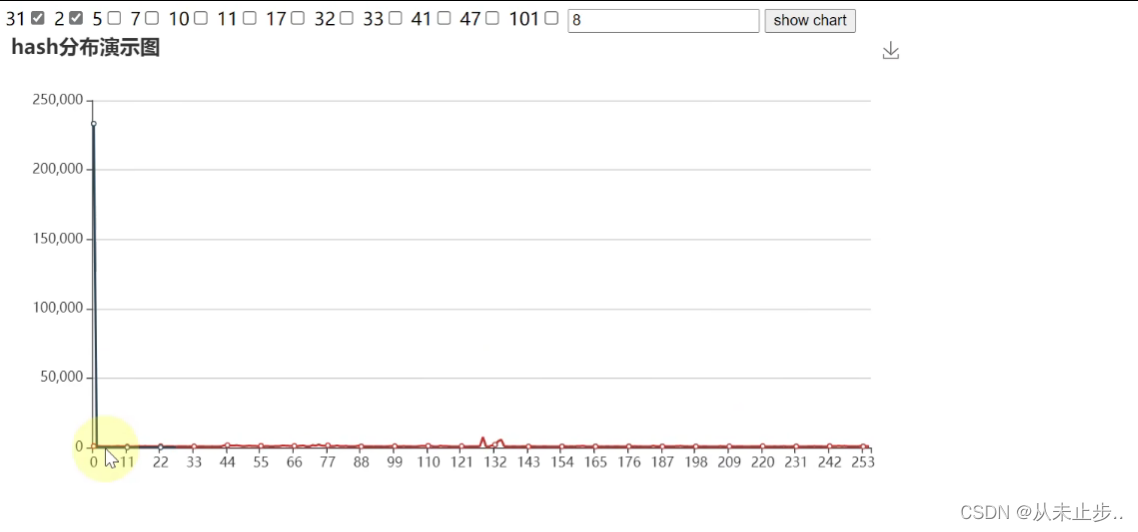
蓝色线条为公式套入11的散列效果如下：
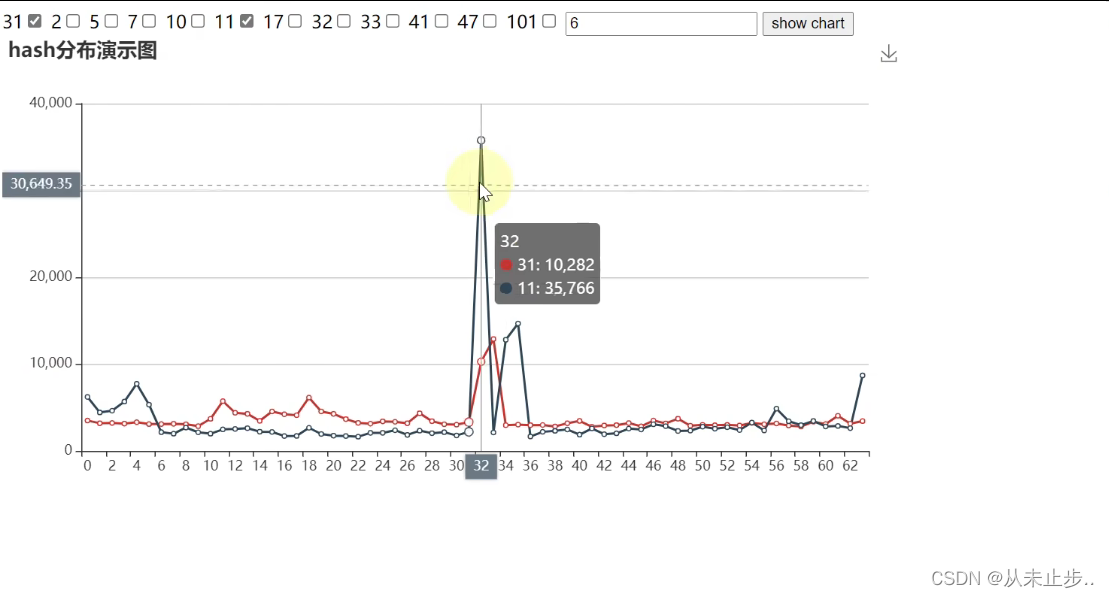
蓝色线条为公式套入41的散列效果如下：
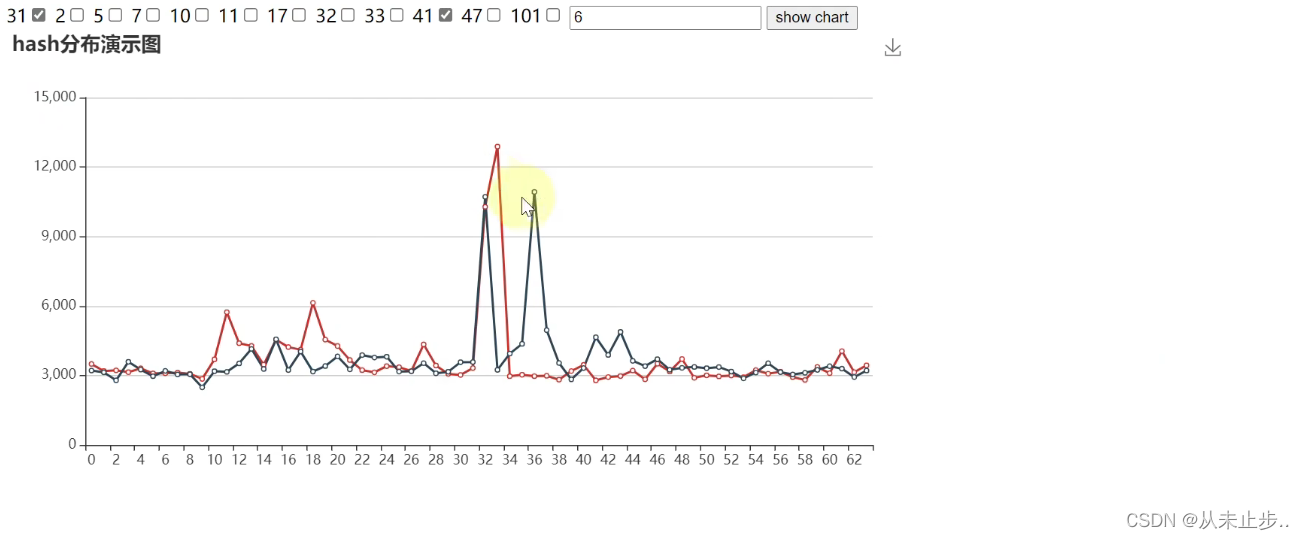
通过上述几组数据的对比，我们不难看出31和41套入公式的散列性是比较好的，那么为什么选择31而不是41呢？
原因是：我们不仅得保证有一个较好的散列性，而且还需要保证经过加减法可以优化为2的n次幂，31就满足，但41并不能满足
