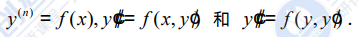趣味三角——第12章—

第12章节 tanx

In his very numerous memoires, and especially in his

great work, Introductio in analysin infinitorum (1748),

Euler displayed the most wonderful skill in obtaining a

rich harvest of results of great interest. . . . Hardly any

other work in the history of Mathematical Science gives

to the reader so strong an impression of the genius of the

author as the Introductio.

(欧拉在他数量众多的回忆录中，尤其是在他的伟大著作<<Introductio in analysin infinitorum>>(无穷小分析引论)(1748 年)中，展示了获得大量有趣结果的绝妙技巧……在数学科学史上,几乎没有任何其他著作能给给予读者能像引论一样，留下如此强烈的作者的天才印象。)

——E. W. Hobson, “Squaring the Circle”: A History of the Problem (“化圆为方”：一个历史问题)(1913)

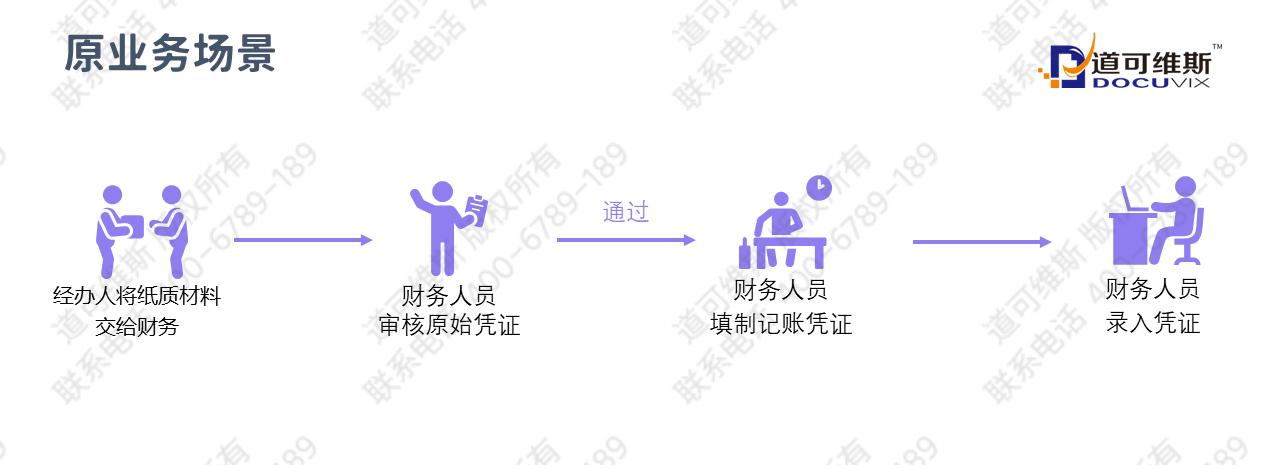
在我们在初级函数中遇到的众多函数中，也许最著名的函数要数正切函数(tangent)。基本事实是众所周知的：f(x) = tan x 在x = nπ(n = ±0, ±1，±2，...)处其值为0,在x = (2n + 1)π/2 (n = ±0, ±1，±2，...)处无限不连续，以及具有周期性(对于一个函数f(x),假如P是使得关系f(x + P ) = f(x)对于函数定义域上的所有x都成立的最小值，则就称函数f(x)为周期函数,其周期为P)，周期为π。最后一个事实非常值得注意：函数 sin x 和 cos x 具有共同的周期 2π，但它们的比率tan x将周期减少为π。当谈到周期性时，函数代数的一般规则可能无效：两个函数 f 和 g 有一个共同的周期 P 并不意味着 f + g 或 fg 也有相同的周期。[1]

正如我们在第 2 章中看到的，正切函数起源于古代的“影子计算(shadow reckoning)”。在文艺复兴时期，它与刚刚兴起的(fledging)透视艺术(透视画法)(art of perspective)相关，虽然当时并没有称之为“切线”，但其确实又复活了(resurrected)。一个物体随着远离观察者而逐渐变小是一种常见的体验。从地面观看高层建筑时，效果尤为明显：随着视角升高，垂直等间距的特征(例如建筑物的地板)似乎逐渐缩短；反之，等量的仰角增量与结构相距越来越远的点相交。著名的纽伦堡艺术家Albrecht Dürer(1471-1528年)是透视法的创始人之一，他的一项研究清楚地表明了这种效果(图 75)。[2]

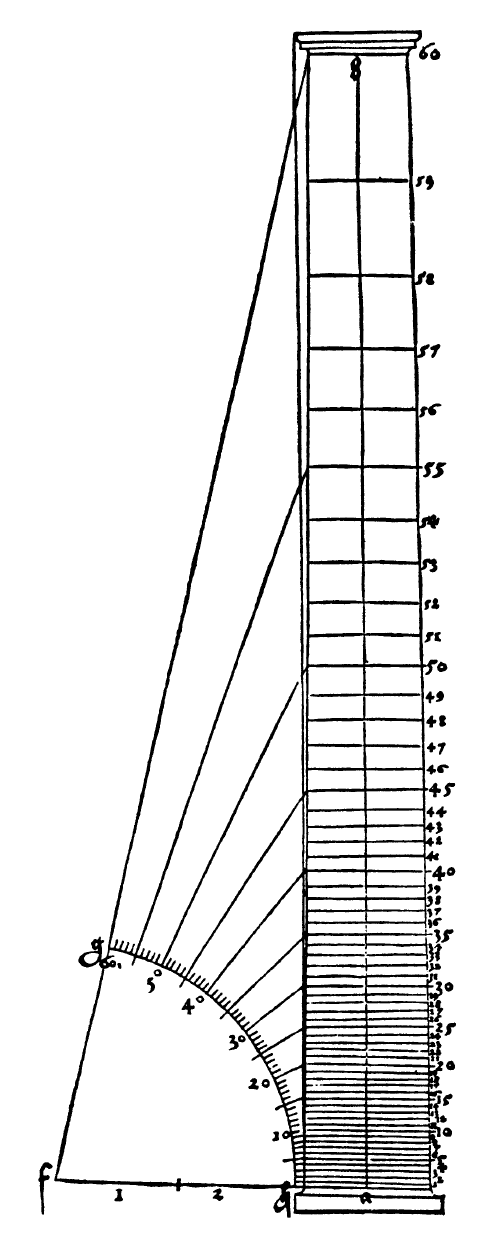
--------------------------图75 Albrecht Dürer的一项研究------------------------

当仰角接近90度并且高度似乎无限制地增加时，Dürer和他的同时代人对这种现象的极端情况特别感兴趣。更有趣的是平面中平行线的行为：当它们远离观察者时，它们似乎越来越近，最终汇聚在地平线上的一个点，称为“消失点(vanishing point)”。所有这些特征都可以追溯到接近 90°的 tan x 的行为。今天，当然，我们说当 x 接近90°时tan x趋于无穷大，而在90°时它是不确定的；但这种微妙之处不为前人所知，直到最近，人们仍然可以在许多三角学教科书中找到“tan 90°= ∞”这一说法。

但是让我们回到世俗的事情上。大约在1580年，Viète 提出了一个美丽的定理，遗憾的是，该定理几乎从今天的教科书中消失了：切线定律(the Law of Tangents)。它说的是，在任何三角形中，

$\frac{a+b}{a-b} = \frac{tan\frac{\alpha+\beta}{2}}{tan\frac{\alpha-\beta}{2}}$ 。---------------------------------------------------------------(1)

这个定理是从正弦定理(a/sin(α)= b/sin(β)= c/sin(γ))以及恒等式

$sin(\alpha) \pm sin(\beta) = 2sin((\alpha\pm \beta)/2) cos((\alpha\mp\beta)/2)$ 推出，但是在Viète时期，它被看作一个独立的定理。[3] 当已知三角形的两条边及其夹角时(SAS——边角边的情况)，可用以求三角形。通常，人们喜欢用余弦定理( $c^{2} = a^{2} + b^{2}-2ab cos(\gamma)$ ) 来求得另一条边，然后使用正弦定理来求得一个角或其它的角。然而，由于余弦定律涉及加法和减法，它并不适合对数计算——实际上它只是在手持计算器问世之前求解三角形(或大多数其他计算)的唯一方法。使用切线法可以避免这一困难：因为已知一个角，比如说γ，你可以求得(α + β)/2,然后在方程(1)以及正切表的帮助下求得(α - β)/2；从这两个结果出发，就可以求得α和β,最后，利用正弦定理就可以求得另外两条未知的边。当然，有了计算器就没有必要了，这或许可以解释为什么切线定律失去了大部分吸引力。尽管如此，它优雅的对称形式应该是一个足够好的理由让它从遗忘中复活，如果不是作为一个定理，那么至少作为一个练习还是有必要的。对于那些喜欢数学“错误(misteakes)”的人——歪打正着(例如16/64 = 1/4)——正切法则为此提供了充裕的(ample)机会: 以方程(1)的右侧开始，“消除”1/2和“tan”,用对应的拉丁字母替换掉希腊字母，则你会得到左侧的部分。[4]

其他涉及 tan x 的公式同样优雅；例如，如果α, β,和γ是任意三角形的三个角，我们有

tan α + tan β + tan γ = tan α .tan β .tan γ ----------------------------------(1)

这个公式可以通过将角度关系写成γ = 180°- (α + β)以及对正切使用加法公式来证明。这个公式的著名之处不仅在于完美的对称性，而且还因为其导致了一个出人意料的结果。来自代数的一个著名的定理说的是，假如 $x_1,x_2,...,x_n$ 是任意正整数, 那么它们的算术平均值永远不会小于它们的几何平均值；即，

$\frac{x_1+x_2+...+x_n }{n}\geq \sqrt[n]{x_{1}.x_{2}.....x_{n}}$

此外，当且仅当 $x_1 = x_2 =...= x_n$ 时，这两个均值相等。我们假设我们的三角形是锐角三角形(acute triangle)，因此，所有三个角都具有正值的正切值，则定理说的是

$\frac{tan\alpha+tan\beta+tan\gamma}{3}\geqslant \sqrt[3]{\alpha.\beta.\gamma}$ 。

但是鉴于等式(2)，这种不等式变为

$\frac{tan\alpha.tan\beta.tan\gamma}{3}\geqslant \sqrt[3]{\alpha.\beta.\gamma}$

不等式两边取立方得到

$tan \alpha .tan \beta .tan \gamma \geq \sqrt{27} = 3\sqrt{3}$ 。

因此，在任意锐角三角形中，三个角的正切之积(以及之和)不小于 $3\sqrt{2} \approx 5.196$ 当且仅当角α = β = γ = 60°时，即三角形为等边三角形时，不等式取得最小值。

如果三角形是钝角(obtuse)，则三个角之一有负切线，在这种情况下定理不适用；然而，由于钝角只能在90°到180°之间变化，因此它的切线范围在区间(-∞，0)内；而其他两条切线保持正值且有限。因此，三个正切的乘积可以取任何负值。

结论是，在任意锐角三角形中，我们有 $tan \alpha .tan \beta .tan \gamma \geq \sqrt{27} = 3\sqrt{3}$ (当且仅当三角形为等边三角形时取得等号),以及在任意钝角三角形中，我们有 $-\infty < tan \alpha .tan \beta .tan \gamma < 0^{\circ}$ 。

角度的倍数的正切为我们提供了有趣公式的另一个来源。在第8章中我们获得了公式

$tan\frac{(n+1)\alpha}{2}=\frac{sin \alpha + sin 2\alpha + sin 3\alpha + ...+ sin n\alpha}{cos \alpha + cos 2\alpha + cos 3\alpha + ...+ cos n\alpha}$

我们可以令α/2 = β，以及n + 1 = m ,改写一下等式，使其略为更加有用；则有

$tan(m\beta)=\frac{sin 2\beta + sin 4\beta + ...+ sin 2(m-1)\beta}{cos 2\beta + cos 4\beta + ...+ cos 2(m-1)\beta}$ 。

但即使是这种形式，该公式的用处也很有限，因为它用其他角度的正弦和余弦表示一个角度的倍数的正切。如果我们能用α的正切(并且单独地，而不是它的倍数)来表示tan nα，那将是可取的(desirable)。幸运的是，这是可以做到的。

我们以正切的加法公式为出发点，

$tan (\alpha + \beta) = \frac{tan (\alpha) + tan(\beta) }{1-tan (\alpha) tan(\beta)}$ 。

从这个基本公式出发，我们得到

$tan (2\alpha) = tan (\alpha + \alpha) = \frac{tan(\alpha) + tan(\alpha)}{(1-tan (\alpha).tan(\alpha)} = \frac{2tan(\alpha)}{1-tan^2 \alpha} ,$

$tan (3\alpha) = tan (2\alpha + \alpha) = \frac{tan(2\alpha) + tan(\alpha)}{(1-tan (2\alpha).tan(\alpha)} = \frac{3tan(\alpha)-tan^{3}\alpha}{1-3tan^3 \alpha} ,$

等等。几步之后，一种模式开始出现：我们发现其系数与 $(1+x)^{n}$ 展开式中x幂项的系数相同——我们熟悉的二项式系数(binomial coefficients)——除了它们以锯齿形模式(zigzag pattern)在分子(numerator)和分母(denominator)之间交替(从分母中的第一项开始)并且它们的符号成对交替。[5] 图76取自19世纪初的三角学教科书，显示了tan 7α以内的模式。考虑到符号，我们可以将系数排列在“帕斯卡正切三角形(Pascal tangent triangle)”中：

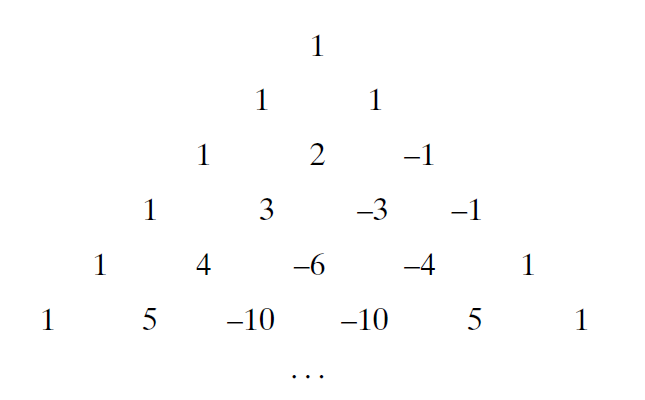
(顶部元素为 1，因为 tan 0 = 0 = 0/1)。我们注意到前两条对角线(从左到右计数)中的所有条目都是正数，接下来两行的所有条目都是负数，依此类推。

--------图76 tan(nα) 的 tan(α) 幂的展开。来自 19 世纪初的三角学书籍。---------

公式中出现的二项式系数似乎与 $(1+x)^n$ 的展开无关，这是De Moivre定理的结果(参见第 83 页)，

$(cos\alpha+isin\alpha)^{n} = cos(n\alpha) + i sin(n\alpha)-----------------(3)$

其中， $i = \sqrt{-1}$ 。如果我们根据二项式定理将式(3)的左边展开，使右边的实部和虚部相等，我们就得到cos(nα)和sin(nα)按 $cos^{(n-k)}\alpha. sin^{k}\alpha$ (其中，k = 0, 1 , 2 , ... , n)表示的表达式；据此，很容易推出tan(nα)的公式；

其中，符号

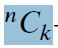
也可以使用 $\binom{n}{k}$ 来表示——表示

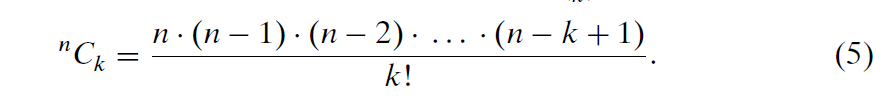
例如，

注意，公式(5)右侧的表达式也等于n!/[k!.(n - k)!]，因此，我们有

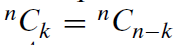
(正如例子中给出来的那样，

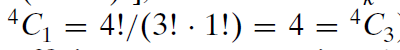
)。由于这个原因，二项式系数是对称的——无论你以x的幂按升序或降序展开 $(1+x)^n$ 它都是一样的。

因为 $(1+x)^n$ 对于正整数数n包括(n + 1)项，出现在等式(4)中的分子和分母的级数是有限项之和，但是，所有6个三角函数也可以通过无限(infinite)表达式来表示，特别是幂级数(power series)和无限积。sin x和cos x的幂级数是

$sin x = x - x^3/3! + x^5/5! - + ...$

和

$cos x = 1 - x^2/2! + x^4/4! - + ...$ 。

牛顿早已知道这些级数，但伟大的瑞士数学家Leonhard Euler(1707-1783年)使用它们得出了大量新结果。Euler将幂级数视为“无限多项式(infinite polynomials)”，它们遵循与普通有限多项式相同的代数规则。因此，他认为，正如n次多项式可以写成形如 $(1-x/x_i)$ (其中， $x_i$ 为多项式的根或者为0 [6])的n个因子(不必相异)的乘积一样，函数sin x也可以写成无限积的形式

$sin x = x (1-x^2/\pi^2)(1-x^2/(4\pi^2))(1-x^2/(9\pi^2))...$ 。------------------------------------------(6)

在这里，每一个二次项 $(1-x^2/(n^2 \pi^2))$ 都是两个线性因子(1-x/(nπ))和(1+ x/(nπ))的乘积，由sin x的零点产生，xn=±nπ ，而单个因子x由x = 0 的零点产生。[7] 如果我们代入x = π/2，方程式 (6) 的一个令人惊讶的结果是：

1 = (π/2).(1-1/4).(1-1/16).(1-1/36)...。

简化每一项并求解π/2 ,我们得到无限项

$\pi/2 = \frac{2}{1} .\frac{2}{3} .\frac{4}{3} .\frac{4}{5} .\frac{6}{5} ....$ 。--------------------------------------------------------------------------------------------(7)

这个著名的公式以John Wallis的名字命名(见第51页), 他在1655年通过大胆的插值(interpolation)过程发现了它。[8]

cos x 的无限积是

$cos(x) = (1-4x^2/\pi^2)(1-4x^2/(9\pi^2))(1-4x^2/(25\pi^2))... ,--------(8)$

其中， $x_i = \pm \pi/2,\pm 3 \pi/2,...$ 是cos x的零值点(此外，在这儿，每个二项式因子都是两个线性因子的乘积)。假如我们现在用等式(8)除以等式(6),我们就得到针对tan x的解析表达式：

$tan(x) = \frac{x (1-x^2/\pi^2)(1-x^2/(4\pi^2))(1-x^2/(9\pi^2))...}{(1-4x^2/\pi^2)(1-4x^2/(9\pi^2))(1-4x^2/(25\pi^2))...}$ 。----------------------(9)

然而，这种表述相当麻烦。为了简化它，让我们使用一种来自积分学中的熟悉技术——将比率函数分解为“部分分数(partial fractions)”。我们将等式(9)的右边表示为分数的无穷和，每个分数的分母等于等式(9)的分母中的一个线性因子:

$tan(x) =\frac{A_1}{(1-2x/\pi)} / + \frac{B_1} {(1+2x/\pi)} + \frac{A_2}{(1-2x/3\pi)} + \frac{B_2}{(1+2x/3\pi) } + ....$ 。---------(10)

为了求得分解式的系数，让我们“清零分数”：我们将等式(10)的两边乘以所有分母的乘积(即乘以cos x)，并将结果等同于等式(9)的分子(即对sin x)：

x(1- x/π)(1+ x/π)(1- x/(2π))(1+ x/(2π))...

=A1 (1+ 2x/π)(1- 2 x/(3π))(1+ 2 x/(3π))...

+ B1(1- 2x/π)(1 - 2 x/(3π))(1 + 2 x/(3π))...

+ ... -----------------------------------------------------------------(11)

请注意，在等式(11)右侧的每一项中，恰好缺少一个因子——等式(10)中相应系数的分母(就像求普通公分母时一样)。

现在，等式(11)在x中是查恒等式——它适用于我们选择置入其中的任何x值。为了求得 $A_1$ ,我们取 $A_1$ = π/2 ；这将“消灭(annihilate)”除第一项以外的所有项，得出

(π/2).(1/2).(3/2).(3/4).(5/4)....

= $A_1$ .2.(2/3).(4/3).(4/5).(6/5)....

对 $A_1$ 解方程，我们得到

$A_1 = (\pi/2).(1/2)^2. (3/2)^2.(3/4)^2. (5/4)^2 ....$

$= (\pi/2). [(\frac{1}{2})(\frac{3}{2})(\frac{3}{4})(\frac{5}{4})....]^2$ 。

但是括号内的表达式正好是Wallis乘积的倒数(reciprocal)，即， $\frac{2}{\pi}$ ，因此，我们有

$A_1 = (\frac{\pi}{2}).(\frac{2}{\pi})^2 = \frac{2}{\pi}$ 。

为了求得 $B_1$ ,在等式(11)中，我们除了令 x = -π/2之外，我们遵循同样的流程；求出 $B_1$

= -2/π = $-A_1$ 。其它的系数可按类似的方式求得；[9] 我们求得 $A_2 = 2/(3\pi) = -B_2$ ， $A_3 = 2/(5\pi) = -B_3$ ，以通式表达为

$A_i = \frac{2}{(2i-1)\pi} = -B_i$ 。

将这些系数放回到等式(10)中并将各项成对组合，我们得到大奖(grand prize)，将tan x 分解为部分分数：

$tan (x) = 8x [\frac{1}{\pi^2-4x^2 } + \frac{1}{9\pi^2-4x^2} + \frac{1}{25\pi^2-4x^2 } + ...]$ 。-------------------------(12)

这个著名的公式直接表明，tan x在 x = ±π/2, ±3π/2,...处无定义；显然，这些正是tan x的垂直渐近线。

既然我们在建立方程式(12)上花费了如此多的精力，那么让我们从中获得一些好处。因为等式对所有除了(2n + 1)πx/2(n = 0,±1,±2,...)之外的都成立x值都成立，现在，让我们代入一些特殊值。我们以x = π/4 开始：

$tan (\pi/4) = 8(\pi/4)[1/(\pi^2-\pi^2/4)+ 1/(9\pi^2-\pi^2/4)+ 1/(25\pi^2-\pi^2/4)+...]$

$= (8/\pi)[1/3 + 1/35 + 1/99 + ...]$ 。

括号中的第一项格式为

$1/[4(2n-1)^2 - 1] = 1/[(4n - 3)(4n -1)]=(1/2)[ 1/(4n-3)- 1/(4n-1)],n=1,2,3,...;$

因此，我们有

1 = (π/4)[1 – 1/3 + 1/5 - 1/7 + - ...] ，

据此，我们得到

$\frac{\pi}{4} = 1-\frac{1}{3} + \frac{1}{5} - \frac{1}{7} +- ...$ 。---------------------------------------(13)

这个著名的公式由苏格兰数学家James Gregory(1638-1675年)于1671年发现，他从反正切的幂级数推导出来。 $tan^{-1}x = x - x^3/3 + x^5/5 - + ...,$

在这个反正切等式中，代入x = 1，得到等式(13)。1674年Leibniz独立发现了同一个公式，所以这个公式也常以他的名字命名。[10] 这是新发明的微积分的第一个成果之一，它让Leibniz非常高兴。

Gregory-Leibniz级数(也是Wallis的乘积)的非凡之处在提示了于π和整数之间出乎意料的联系。然而，由于其收敛速度非常慢，从计算的角度来看，该级数几乎没有用处：它需要628项才能将π逼近到小数点后两位——同样使用穷尽法，其精度远低于阿基米德(Archimedes)在两千多年前使用该方法获得的精度。尽管如此，Gregory-Leibniz级数标志着数学史上的一个里程碑，它是未来几年将要发现的众多涉及π的无限级数中的第一个。

下一步，我们用x = 1 代入等式(12)，我们得到：

$tan (\pi) = 8\pi[1/(-3\pi^2) + 1/(5\pi^2)+ 1/(21\pi^2)+...]$ 。

消掉(8/π)并将负项移到等式的左侧，我们得到

1/5 + 1/21 + 1/45 + ... = 1/3 。

或许有些令人失望的是，我们得到了一个不涉及π的级数，但是当我们尝试将 x = 0代入等式(12)时，我们的兴奋又回来了。起初我们只是得到不定方程 0 = 0，但我们可以通过将等式两边除以 x 然后让 x 趋近于零来解决这个困难。在左边我们得到

$\lim_{x->0}\frac{tan(x)}{x} = (\lim_{x->0}\frac{sin(x)}{x})(\lim_{x->0}\frac{1}{cos(x)})= 1.1 = 1$ 。

因此，等式(12)成了

$1 = (8/\pi^2)[ \frac{1}{1} + \frac{1}{9} + \frac{1}{25} + ...]$

或

$\frac{\pi^2}{8} = \frac{1}{1^2} + \frac{1}{3^2} + \frac{1}{5^2} + ...$ 。---------------------------------(14)

最后一个公式与Gregory-Leibniz级数一样引人注目，但我们可以从中推导出一个更有趣的结果。我们将再次以一种非严格的方式来做这件事，本着(in the spirit of)Euler大胆探索无限级数世界的精神(更严格的证明将在第 15 章中给出)。我们的任务是找出所有正整数(偶数和奇数)的平方的倒数之和；让我们用 S 表示这个和：[12]

$S = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} ...$

$= (\frac{1}{1^2} + \frac{1}{3^2} + ...) + (\frac{1}{2^2} + \frac{1}{4^2} + ...)$

$= (\frac{1}{1^2} + \frac{1}{3^2} + ...) + \frac{1}{4}(\frac{1}{1^2} + \frac{1}{2^2} + ...)$

$= \frac{\pi^2}{8} + \frac{1}{4}S$

据此，我们得到 $\frac{3}{4}S=\frac{\pi^2}{8}$ ,最后

$S = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} ...= \frac{\pi^2}{6}$ 。---------------------------------(15)

等式(15)是所有数学中最著名的公式之一；它是Euler在1734年灵机一动中发现的，它挑战了所有现代严格标准。它的发现解决了18世纪的一个重大谜团：一段时间以来，人们就知道级数收敛，但它的总和的值却让当时最伟大的数学家望而却步，其中包括伯努利(Bernoulli)兄弟。[13]

我们考虑Euler发现的另一个无穷级数。我们从余切的双角公式开始，

$cot (2x) = \frac{1-tan^2 (x)}{2tan(x) }= \frac{cot(x)-tan(x)}{2}$ 。

以 x ≠ (nπ)/2的任意角重复应用到公式，我们得到

$cot(x) = \frac{1}{2}(cot\frac{x}{2} - tan \frac{x}{2})$

$= \frac{1}{4}(cot\frac{x}{4} - tan \frac{x}{4})-\frac{1}{2}tan\frac{x}{2}$

$= \frac{1}{8}(cot\frac{x}{8} - tan \frac{x}{8})- \frac{1}{4}tan\frac{x}{4}- \frac{1}{2}tan \frac{x}{2}$

=...

$=\frac{1}{2^n} (cot \frac{x}{2^n} - tan\frac{x}{2^n}) - \frac{1}{2^{n-1}} tan \frac{x}{2^{n-1}} -...- \frac{1}{2}tan \frac{x}{2}$ 。

随着n->∞， $\frac{cot \frac{x}{2^n}}{2^n}$ 趋近于 $\frac{1}{x}$ [14]，因此，我们得到

$cot x = \frac{1}{x}-\sum_{n=1}^{\infty}\frac{1}{2^n}tan\frac{x}{2^n}$

或

$\frac{1}{x} - cot (x) = \frac{1}{2} tan\frac{x}{2} + \frac{1}{4}tan\frac{x}{4} + \frac{1}{8} tan\frac{x}{8} + ...$ 。-----------------------(16)

这个鲜为人知的公式是从Euler的想象力中浮现出来的数百个涉及无限过程的公式之一。在它的背后隐藏着一个惊喜：如果我们代入 $x = \frac{\pi}{4}$ ，我们得到

$\frac{4}{\pi} - 1= \frac{1}{2} tan\frac{\pi}{8} + \frac{1}{4} tan\frac{\pi}{16} + ...$ 。

用 $tan \frac{\pi}{4}$ 替换掉左侧的1，并将所有正切换移到等式右侧，等式再除以4，我们得到

$\frac{1}{\pi} = \frac{1}{4} tan\frac{\pi}{4} + \frac{1}{8} tan\frac{\pi}{8} + \frac{1}{16} tan\frac{\pi}{16} + ...$ 。-----------------------(17)

等式(17)在数学中肯定是最美的，但它几乎没有出现在教科书中。此外，右侧的级数收敛得非常快(请注意，系数“和”角度每项按1/2倍递减)，因此我们可以使用等式(17)作为一种近似π值的有效方法：它只需要十二项即可取得小数点后6位精度，即百万分之二；再增加四项将使准确度提高到十亿分之一。[15]

我们遵循Euler的精神来处理等式(6)和(9)，就好像它们是有限的表达式一样，服从普通代数的规则。Euler生活在一个无忧无虑的数学探索时代，那时对无穷级数的正式操作是一种正常的做法；收敛和极限问题尚未得到充分理解，因此大体上被忽略了。今天我们知道这些问题对所有无限过程都至关重要，忽视它们会导致错误的结果。[16] 引用一句George F. Simmons在他出色的微积分教科书中的话：“这些大胆的猜测是Euler独特天赋的特征，但我们希望没有学生会认为它们具有严格证明的力量(These daring speculations are characteristic of Euler’s unique genius, but we hope that no student will suppose that they carry the force of rigorous proof)。” [17]

注释和资源来源：

1. 这种情况的一个简单例子是函数f(x) = sinx ,g(x) = 1 – sinx 。其每个函数的周其都是2π，而它们的和 f(x) + g(x) = 1 ，是一个常量，任意实数都可作为其周期。

2. 关于Dürer的数学著作，请参见Julian Lowell Coolidge的<<The Mathematics of Great Amateurs>>(伟大的数学业余爱好者)( 1949 年初版; New York: Dover, 1963年重印)第 5 章,以及Dan Pedoe 的著作<<Geometry and the Liberal Arts>>(几何与人文科学)( New York: St. Martin’s Press,1976年版) 第2章。

3. 这个法则的一个等价形式，其中等式的左侧用(sinα + sinβ)/( sinα + sinβ)替换, Regiomontanus 在1464 年左右就已经知道了，但奇怪的是他并没有在他的主要论文<<On Triangle>>(论三角形)(见第44页)中包括它——也没有包括正切函数的任何其他应用。至于正切法则的其它发现，参见David Eugene Smith的<<History of Mathematics>>(数学史)(1925初版; New York: Dover, 1958重印)。

4. 三角学中大量存在(abounds)这样的例子。在第8章中我们已经见到了一个与 sinα + sin(2α) + ... + sin(nα) 的求和公式相关的内容。另一个例子是恒等式

$sin^{2}\alpha - sin^{2}\beta = sin(\alpha + \beta).sin(\alpha - \beta)$ ,

可通过将左侧写成

$sin(\alpha^2-\beta^2) = sin[(\alpha + \beta).(\alpha -\beta)] = sin(\alpha + \beta).sin(\alpha - \beta)$ 的方式予以“证明”。

5. 我们可以考虑将 $(1+ix)^{n}$ (其中 $i=\sqrt{-1}$ )扩展来考虑符号。

6. 这相当于更熟悉的形如(x - xi)因式分解成的因子。例如，多项式

$f(x) = x^2 - x - 6$ 的函数零值点是-2和3 ，因此，我们有f(x) = (x + 2)( x - 3) = -6(1 + x/2)( 1- x /3)。一般地，多项式 $f(x) = a_n x^n + a_{n-1} x^{n-1} + ... + a_1x + a_0$ 可以写成 $a_n(x-x_1)..... (x-x_n)$ (其中 $a_n$ 是前导系数)，或写成 $a_0(1-x/x_1)..... (1-x/x_n$ )(其中， $a_0$ 是常数项)。

7. 实际上，Euler丢弃了x = 0 的根，并因此获得了 $\frac{sin(x)}{x}$ 的无限积。参见Morris Kline的著作<<Mathematical Thought from Ancient to Modern Times>>(古今数学思想)( New York: Oxford University Press, 1972年版)卷2第448-449页。

8. 参见<<A Source Book in Mathematics>>(一部数学原始资料书),1200-1800年，编辑D. J. Struik(Cambridge, Mass.: Harvard University Press, 1969年版)，第244-253页，对于等式(6)和(7)的严密证明，参见Richard Courant的著作<<Differential and Integral Calculus>>(微积分)( London: Blackie & Son, 1956年版),卷1第444-445页和223-224页。π的其它无限积也可以通过等式(6)推断；例如，代入 x = π/6，我们得到

$\frac{\pi}{3} = \frac{6}{5} . \frac{6}{7} .\frac{12}{11} . \frac{12}{13} . \frac{18}{17} . \frac{18}{19} .... = \prod_{n=1}^{\infty}(6n)^{2}[(6n)^{2}-1]$ ，

它实际上比Wallis积收敛得更快(与Wallis积的 493 项相比，该积近似π接近小数点后两位需要55项)。

9. 然而，随着 i 的增加，所得的数值积变得更加复杂。幸运的是，有一种更简单的方法可以找到系数：等式(11)的左侧是 sinx，而右侧的每一项等于cosx 除以该项缺失的分母。因此，为了求得 $A_2$ ，在等式(11)中代入 x = 3π/2；这将“消灭掉(annihilate)”除A2的所有项，因此，我们得到剩下的项 $sinx_{x = \frac{3\pi}{2}} = A_2 [\frac{cos(x)}{1-2x/(3\pi)) }]_{x = \frac{3\pi}{2}}$ 。

左侧等于-1，但是，在右侧我们得到了不确定表达式 00 。为了计算它，我们使用洛必达法则(L'Hospital's Rule)并将其转换为 $A_2 [(-sinx)/(-2/(3\pi))]_{x = 3\pi/2} = -(3\pi/2) A_2$ 。

因此，我们求得 $A_2 = 2/(3\pi)$ 。以同样的方式可以求得其它系数。

10. 参见Petr Beckmann的著作<<A History of π>>(数π的历史)( Boulder, Colo.: Golem Press,1977)，第132-133页；对于Leibniz的证明，参见George F. Simmons的著作<< Calculus with Analytic Geometry>>(带解析几何的微积分)( New York: McGraw-Hill, 1985)，第720-721页。 $tan^{-1}x$ 的级数可以通过将表达式 $1/(1+x^2)$ $1 - x^2 + x^4 - + ...$ 写成幂级数(具有商- $x^2$ 的几何级数)并逐项融合的方式求得。

11. 级数 1/5 + 1/21 + 1/45 + ...收敛于1/3, 注意到，其每一项符合通式

$1/[(2n+1)^2-4] = 1/[(2n-1)(2n+3)] = (1/4)[1/(2n-1)- 1/(2n+3)]$ ，这可以确认其收敛于1/3；因此，级数变成了(1/4)[(1-1/5) + (1/3-1/7) + (1/5-1/9) + (1/7-1/11) + ...]。这是一个“套叠式(telescopic)”的级数，在其中，除了第一项和最后一项，其它所有项都被消掉了，最终和为(1/4)(1 + 1/3) = 1/3 。

12. 当然，假设该级数收敛。在微积分课本中，证明了级数 $\prod_{n=1}^{\infty}1/n^k$ (其中 k 是一个实数)对于所有 k > 1 的实数收敛，而对于所有 k ≤1 的实数发散,这里对应的情况是 k = 2，因此 S 收敛。

13. 参见Simmons的<<Calculus>>(微积分)第722-726页(Euler的证明)以及723-725(一种严密的证明)。有人会认为级数 $\prod_{n=1}^{\infty}1/n^2$ 比 Gregory-Leibniz 级数收敛得快，理由是其所有项都是正值且包括整数平方。让人诧异的是，事实并非如此：其占到 628 项才能近似到π的小数点后两位精度，而Gregory-Leibniz 级数近似到π的小数点后两位精度需要600 项。

14. $\lim_{n->\infty}\left \{ \left [ cot \frac{x}{2^n}\right ] /2^n \right \} = (1/x)\lim_{n->\infty}\left [ (\frac{x}{2^n}) / cot (\frac{x}{2^n})\right ] = (1/x)$ ，最后的结果推断于

$\lim_{t->\infty}(\frac{1}{t})/cot(\frac{1}{t}) = \lim_{u->0} cot(u) = \lim_{u->0}(u)/tan(u) = 1$ ，

其中，u = 1/ t。

15. 有人会质疑等式(17)根据自己来表达π，因为切线项中的角度以弧度表示。但是，三角函数不受角度单位选择的影响；使用度数而不是弧度，等式(17)变为 1/π = (1/4)tan 45°+ (1/8)tan (45°/2) + ...。

16. 关于这个主题，参见Kline的“数学思想”卷2第442-445页以及460-467页。另可参见我的另一本书<<To Infinity and Beyond: A Cultural History of the Infinite>>(无限与超越：无限的文化史) (Princeton, N.J.: Princeton University Press, 1991年出版)第32-33页以及36-39页。

17. Simmons的“微积分”的第723页。

内容来源：

<<Trigonometric Delights>> 作者：Eli Maor