正则表达式是如何运作的？

在日常的开发工作当中，我们必不可免的会碰到需要使用正则的情况。

正则在很多时候通过不同的组合方式最后都可以达到既定的目标结果。比如我们有一个需要匹配的字符串：

hello

，我们可以通过 /

./ 以及 /

.?/ 来匹配，两种方式就像就像中文语法中的陈述句以及倒装句，不同的语序往往不影响我们的理解，但是他们的运作方式却完全不一样。

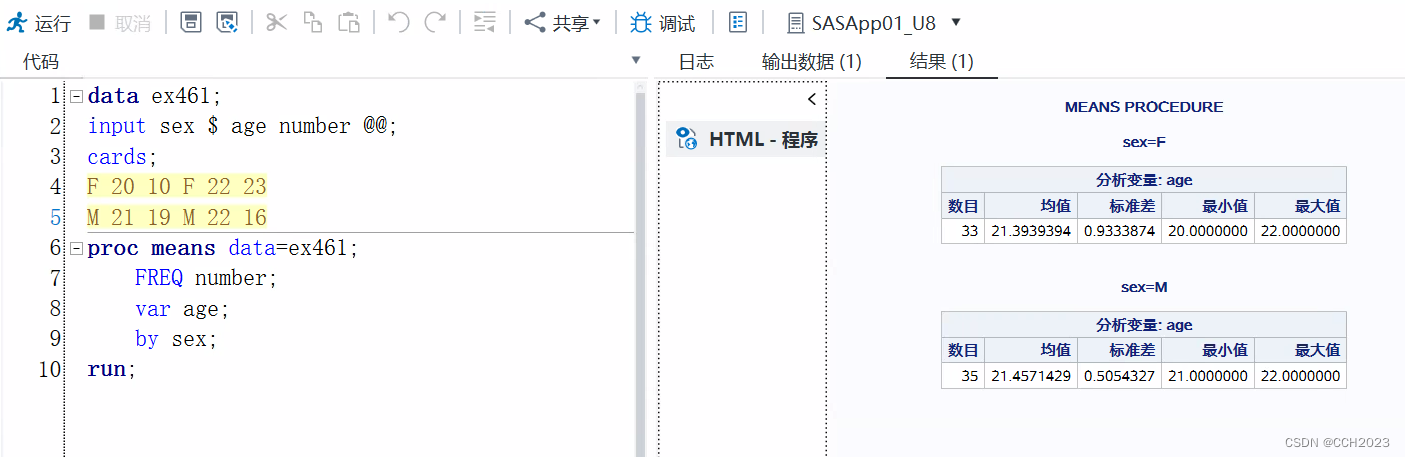
为了让大家有一个更加直观的感受，这里将

hello

分三次存到一份百万字符文档的最前面，中间以及最后面，然后分别使用上面的 2 个正则表达式进行匹配，并测算匹配到对应字符所需要的时间，结果如下（实验结果通过 https://regexr.com/ 得出）：

最前面中间最后面
/

./ 1.1ms 0.7ms 0.2ms
/

.?/ 0.1ms 0.2ms 0.3ms
由此我们可以明显地看出不同的撰写方式，匹配的效率也有很大的不同。

撰写正则是一个不断思考与抉择的过程。就像一道数学题中往往包含一种或几种最优解的可能，想要趋近这个结果，就需要我们理清题意，掌握正则的表达方式以及加强对正则运作方式的理解。

那么，我们应该如何趋近最优解，养成良好的撰写习惯，锻炼撰写健壮的正则表达式的能力呢？

知己知彼，百战不殆，要写好正则表达式就需要做到知其然还要知其所以然。因此，本文将尝试从正则原理的角度出发，介绍正则匹配的规则，梳理正则与有限自动机的关系、及有限自动机之间的转化逻辑，并解释回溯等相关概念。希望能够帮助大家更好地理解及使用正则。

正则表达式与有限自动机（FA）
正则表达式是建立在有限自动机 ( Finite Automaton ) 的理论基础上的，是自动机理论的应用。当我们写完相关的表达式之后，正则引擎会按照我们所写的表达式构建相应的自动机，若该自动机接受输入的文本并抵达最终状态，则表示输入的文本可以被我们所写的正则表达式匹配到。

有限自动机的图示
自动机的图形化包含以下元素：

箭头：表示路径，可以在上面标注字母，表示状态 1 经过该字母可以转换到状态 2 （也可以是标注 ε，即空串，表示无需经过转换就可以从状态 1 过渡到状态 2），
单圆圈：表示非结束的中间状态
双圆圈：表示结束状态
由自身指向自身的箭头：用于表示 Kleene 闭包（也就是正则表达式中的），指可以走任意次数的路径。
以 abc 这条正则表达式为例，其有限自动机的图示如下，表示状态 1 经过 a 可以过渡到状态 2 ，在状态 2 可以经过 ε 再循环经过 b 也可以不经过 b 而直接通过通过 ε 再经由 c 过渡到最终的结束状态。

不确定有限自动机（NFA）及确定有限自动机（DFA）
有限自动机又可以分为 NFA：不确定有限自动机（Nondeterministic Finite Automaton ）及 DFA：确定有限自动机（Deterministic Finite Automaton ），NFA 的不确定性表现在其状态可以通过 ε 转换以及对同一个字符可以有不同的路径。而 DFA 可以看作是一种特殊的 NFA，其最大的特点就是确定性，即输入一个字符，一定会转换到确定的状态，而不会有其他的可能。

以 ab|ac 这条正则表达式为例子，我们可以得到以下 NFA 及 DFA 两种自动机。

可以看到自动机 1 中我们有两条路径都是 a，经由 a 可以到达下一个状态，而自动机 2 中只有一条路径，对于图一来说，经由相同的 a 路径却可以导致不同的结果，这即是 NFA，具有不确定性。而对图二来说，其路径都是通往明确的结果，具有确定唯一性，所以是 DFA。

正则替换成 NFA
从上面的图中我们可以看出 DFA 的匹配路径比 NFA 要少且匹配的速度要更快，但是目前大多数的语言中的正则引擎使用的却是 NFA，为什么不直接使用 DFA 而要使用 NFA？为了解答这个问题，我们需要知道如何通过正则转化成 NFA，而 NFA 又可以怎样转成 DFA。

正则表达式转 NFA 主要基于以下 3 条规则（R 表示正则表达式）

连接 R = AB

选择 R = A|B

重复 R = A*

其他的运算基本都可以通过以上三种运算转换得到，比如 A+ 可以用 AA* 来表示

Thompson 算法
为了更好地理解上面的 3 条转换规则，这里介绍比较实用且容易理解由 C 语言 & Unix 之父之一的 Ken Thompson 提出的 Thompson 算法。其思想主要就是通过简单的表达式组合成复杂的表达式。

Thompson算法中两种最基本的单元（或者说两种最基本的 NFA）:

表示经过字符 a 过渡的下一个状态以及不需要任何字符输入的 ε 转换过渡到下一个状态。

对于连接运算 R = AB，我们将 AB 拆解成 NFA(A) 与 NFA(B) 两个单元，然后进行组合：

对于选择运算 R = A｜B，我们同样将 A 与 B 拆解成 NFA(A) 与 NFA(B) 两个单元，然后进行组合：

对于重复运算 R = A*，其表示可能不需要经过转换，可能经过 1 次或者多次，所以拆解成单一 NFA 后，我们可以这样表示：

由此，我们就可以根据上面的 3 条转换规则，将正则表达式进行拆分重组，最后得出相应的 NFA。

NFA 转换成 DFA 及其简化
DFA 实际上是一个特殊的 NFA，转 DFA，就是要将 NFA 中将所有等价的状态合并，消除不确定性。

这里以《编译原理》一书中的一道例题来完整地讲解一下如何从正则转 NFA 再转成相应的 DFA，并对其进行简化。

eg: (a|b)(aa|bb)(a|b)
这里我们依据正则转 NFA 的三条规则以及 Thompson 算法的理念，将上述的表达式进行拆分与组合：

首先我们将该表达式以括号为分隔，视为 3 个正则表达式子通过连接符连接，以此拆分成 3 个表达式并将其组合
然后根据每个表达式括号内的内容继续拆分成更细的单元，碰到运算符号，则按照规则进行转换，以此类推直到 NFA 变成变成由最小单元组合而成。

子集构造算法
正如前面所说，NFA 转 DFA 本质是将等价的状态合并，消除不确定性。要找出等价的状态，我们需要先找出各个状态的集合。

上面的表达式只有 a 跟 b 两个字符，所以我们要得出各个状态经过 a 以及经过 b 的所有集合，然后再将等价的集合合并。这里先画出所有集合构成的转换表单，结合图示将更有助于我们的的理解。

I Ia Ib
{i,1,2} {1,2,3} {1,2,4}
{1,2,3} {1,2,3,5,6,f} {1,2,4}
{1,2,4} {1,2,3} {1,2,4,5,6,f}
{1,2,3,5,6,f} {1,2,3,5,6,f} {1,2,4,6,f}
{1,2,4,5,6,f} {1,2,3,6,f} {1,2,4,5,6,f}
{1,2,4,6,f} {1,2,3,6,f} {1,2,4,5,6,f}
{1,2,3,6,f} {1,2,3,5,6,f} {1,2,4,6,f}
图示第一列主要是放置所有不重复的集合，第二列表示经过 a 的集合，第三列表示经过 b 的集合

子集构造法寻找集合的规则为碰到一个字符，如果这个字符后面有可以通过空串（ε转换）到达下一个状态，则下一个状态包含在该集合中，一直往后直到碰到一个明确的字符

从上面构造的NFA的初始状态 i 开始，其经过 2 个 ε转换转换可以到达 2 状态，此后必须经过 a 或者 b，由此我们可以得到第一个状态集合 {i,1,2}

从第一个集合开始，分析集合内分别经过 a 和 b 可以达到什么状态，可以看到初始集合中 i 只经过空串，不经过 a、b，状态 1 经过 a 可以到达它自身，也可以再经过 ε 到达状态 2，2 经过 a 只能到达状态 3

据此我们得到初始集合经过 a 的集合为 {1,2,3}，同样的，初始集合经过 b 只在状态 2 与经过 a 不同，所以我们可以得到经过 b 的集合为 {1,2,4}
因为 {1,2,3}，{1,2,4} 都没有出现过，所以这里我们将其记到第一列的第二与第三行，并分析它们经过 a 与 b 的集合。
以此类推直到获得上述所有集合构成的转换表单（完整文字版推导过程附于文末附录）
可以看到上面的转换表的第一列中一共有 7 个集合，这里我们给第一列的集合进行排序（为方便与 NFA 对比，这里将序号 0 改为 i），并对右边经过 a 跟经过 b 的所有集合根据左边的序号进行标记，可以得到相应转换矩阵:

I Ia Ib
{i,1,2} i {1,2,3} 1 {1,2,4} 2
{1,2,3} 1 {1,2,3,5,6,f} 3 {1,2,4} 2
{1,2,4} 2 {1,2,3} 1 {1,2,4,5,6,f} 4
{1,2,3,5,6,f} 3 {1,2,3,5,6,f} 3 {1,2,4,6,f} 5
{1,2,4,5,6,f} 4 {1,2,3,6,f} 6 {1,2,4,5,6,f} 4
{1,2,4,6,f} 5 {1,2,3,6,f} 6 {1,2,4,5,6,f} 4
{1,2,3,6,f} 6 {1,2,3,5,6,f} 3 {1,2,4,6,f} 5
转换矩阵
S a b
i 1 2
1 3 2
2 1 4
3 3 5
4 6 4
5 6 4
6 3 5
依据转换矩阵，我们把第一列的数据作为每一个单独状态，并以 i 为初始状态，由矩阵可得，其经过 a 可以到达状态 1，经过 b 可以到达状态 2，同时我们将包含 f 的集合作为终态（即序号 3，4，5，6），以此类推，我们可以得到如下的 NFA：

因为该 NFA 不包含空串，也没有由一个状态分出两条相同的分支路径，所以该 NFA 就是上述表达式的 DFA。但该 DFA 看起来还比较复杂，所以我们还需要对其进一步简化。

Hopcroft 算法化简
Hopcroft 算法是1986年图灵奖获得者 John Hopcroft 所提出的，其本质思想跟子集构造法相似，都是对等价状态的合并。

Hopcroft 算法首先将未化简的 DFA 划分成终态集和非终态集（因为这两种状态一定不等价），之后不断进行划分，直到不再发生变化。每轮划分对所有子集进行。对一个子集的划分中，若每个输入符号都能把状态转换到等价的状态，则两个状态等价。

这里依据 Hopcroft 算法将上述 DFA 以终态以及非终态进行划分，可以得到 {i,1,2} 以及 {3,4,5,6} 两个集合。然后分别分析两个集合是否能够进一步划分。

集合 {i,1,2} 经过 a 可以得到状态 1 和 3，3 不在集合 {i,1,2} 中，依据矩阵图，我们可以看到 i 和 2 经过 a 都到状态 1，1 经过 a 可以达到状态 3，于是我们将 {i,1,2} 划分成 {i,2} 和 {1} 两个集合

因为 {1} 已经是最小集合，所以无法继续划分，所以分析 {i,2} 集合经过 b 的情况，{i,2} 经过 b 可以达到状态 2 和 4，4 同样不在集合中，所以需要对 {i,2} 进行划分，依据矩阵表，我们可以划分成 {i}，{2}，至此，非终态已经无法往下拆分，所以分析结束，我们得到的拆分集合为 {i}，{1}，{2}

终态集合 {3,4,5,6} 经过 a 可以达到状态 3 和 6，3 和 6 都在集合内部，所以无需往下拆分，经过 b 可以达到状态 4 和 5，4 和 5 同样都在集合内，无需拆分。所以我们可以将 {3,4,5,6} 当作是一个整体。

将集合 {3,4,5,6} 当作一个整体，记成状态 3，重新梳理上面的矩阵，并将所有指向 3，4，5，6 的路径都指向新的状态 3，我们可以得到新的也是最简单的 DFA：

从上面的转换过程可以看到，实际上，NFA 转 DFA 是一个繁琐的过程，如果正则采用 DFA 引擎，势必会消耗部分性能在 NFA 的转换上，而这个转换的效益很多时候远不比直接用使用 NFA 高效，同时 DFA 相对来说没有 NFA 直观，可操作空间也要比 NFA 少，所以大多数语言的采用 NFA 作为正则的引擎。

回溯
正则采用的是 NFA 引擎，那么我们就必须面对它的不确定性，体现在正则上就是回溯的发生。

遇到一个字符串，NFA 拿着正则表达式去比对文本，拿到一个字符，就把它与字符串做比较，如果匹配就记住并继续往下拿下一个字符，如果后面拿到的字符与字符串不匹配，则将之前记下的字符一个个往回退直到上一次出现岔路的地方。

假设现在有一个正则表达式 ab|ac，需要匹配字符串 ac。则 NFA 会先拿到正则的字符 a，然后去比较字符串 ac，发现匹配中了 a，则会去拿下一个字符 b，然后再匹配字符串，发现不匹配，则回溯，吐出字符 b，回到字符 a，取字符 c 去匹配字符串，发现匹配，完成比对。

文字或许比较枯燥，这里用下面得图示来表示上述的过程，蓝色圆圈表示NFA拿到正则的字符后去匹配字符串看是否可以过渡到下一个状态，同时字符的颜色变化表示是否可以被匹配中：

贪婪模式与惰性模式对比
回到一开始讲的通过 /

./ 以及 /

.?/ 来匹配

hello

的问题，因为量词的特殊性以及回溯的存在，所以2种方式的匹配效率也不一样。

表示重复零次或多次，一般情况下会以贪婪模式尽可能地匹配多次，因此在上面的匹配过程中，它会在匹配到
之后一口气把之后的字符也吞并掉，然后通过回溯匹配 < 字符直到匹配到完整的 ，而当我们给 * 加上 ? 之后，它就变成非贪婪的惰性模式，当匹配到
之后它就会通过回溯逐步去匹配 直到匹配中完整的字符串。

目标字符串：

hello

在两个表达式下的匹配过程：

表达式：/

./ 表达式：/

.?/
< 匹配 < < 匹配 <

表达式：ab
aaa 匹配 a
aaa 匹配 b
aa 回溯
aa 匹配 b
a 回溯
a 匹配 b
回溯
这个正则表达式回溯到最后也没有匹配到对应的字符串，而通常我们所写的正则并不单单像例子中只回溯这一小部分，设想一下，一个需要多处回溯的正则表达式子，去匹配成百上千甚至上万个字符，那对机器来说是多么可怕的一件事情。https://www.ixigua.com/7202959346417074688