一、背包问题概述

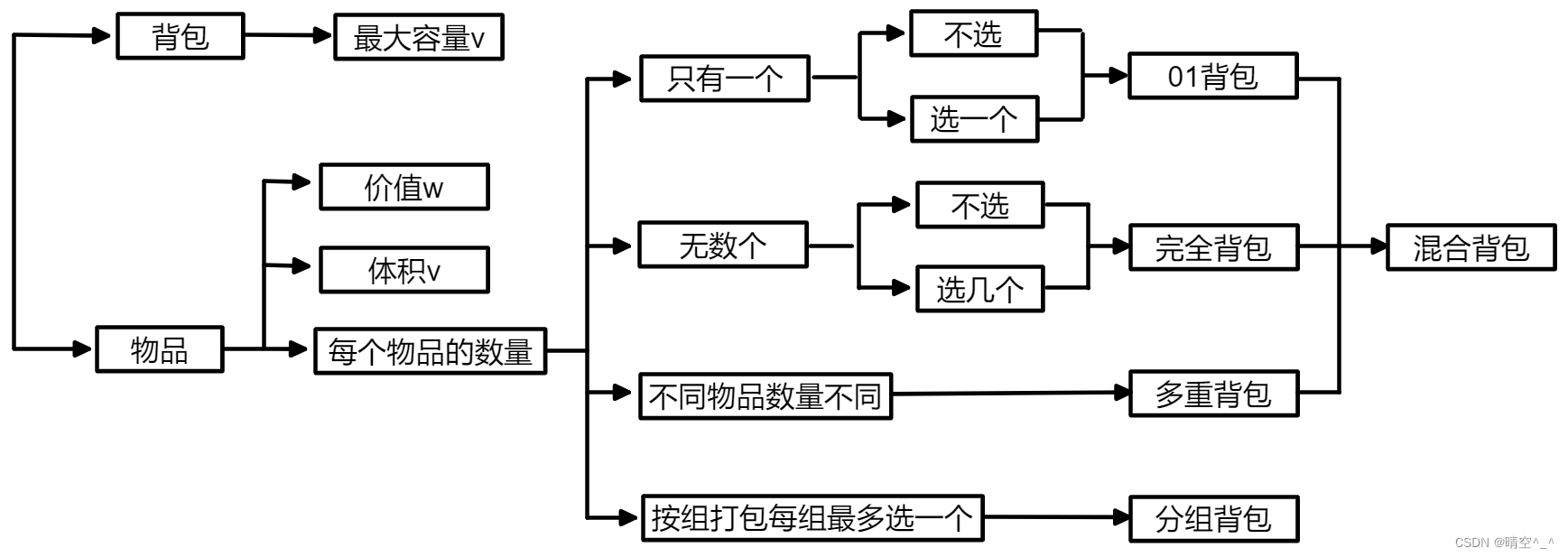
如图，完全背包与01背包的区别只有一点：01背包中每个物品只能取一个而完全背包中每个物品可以取无数个。解决完全背包问题必须首先弄明白01背包，不清楚的可以看我的这篇文章01背包—动态规划。

二、例题

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

背包最大容量为4。

每一个物品有两个状态，“取”或者“不取”。利用回溯法可以暴力枚举所有物品的状态的排列组合状态，与背包最大容量比较就可以求得最大的价值，时间复杂是$O(2^n)$为指数级别，故需要动态规划的解法来进行优化。

三、一维数组（滚动数组）解完全背包

1. 从01背包到完全背包

由01背包—动态规划，我们可以得知一维DP数组是二维DP数组的简化。所以，二维DP数组与一维DP数组在本质上一样的，本文只介绍一维DP数组解完全背包。

对于01背包来说，内循环j是从大到小倒叙遍历的，这样做的原因是防止dp[j]前的元素被污染，避免累加的问题（每个物品只能选一次）。而对于完全背包来说，每个物品可以选择无数次，j从前向后遍历就是对每个容量j都尝试放入物品i看会不会使总价值变大，其本身并不关注放入物品i的个数。所以，完全背包与01背包的代码只有一个区别，就是j的遍历顺序。

// 01背包遍历
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

// 完全背包遍历
// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

2. 01背包与完全背包的不同—遍历顺序

01背包的遍历顺序为：

二维DP数组中，先遍历物品或先遍历背包容量都可以；

一维DP数组中，必须先遍历物品在遍历背包容量。只有这样才能确保每个物品只选一次。

对于完全背包，没有了只能选一次的限制，那么先遍历背包容量再遍历物品可不可以呢？答案是可以的。因为dp[j] 是根据下标j之前所对应的DP数组元素计算出来的。 只要保证下标j之前的DP数组都是经过计算的就可以了。图一是先遍历背包容量再遍历物品；图二是先遍历物品，再遍历背包容量。

// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

// 先遍历背包，再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        if (j - weight[i] >= 0) 
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}