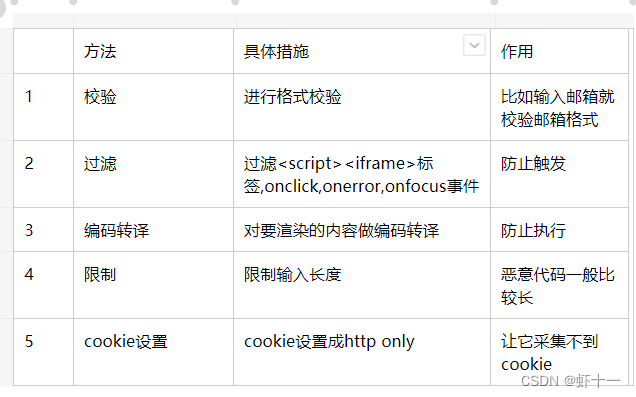
文章目录
- 顶点
- 棱
- 实现正二十面体
plotly 的 Python 软件包是一个开源的代码库,它基于 plot.js,而后者基于 d3.js。我们实际使用的则是一个对 plotly 进行封装的库,名叫 cufflinks,能让你更方便地使用 plotly 和 Pandas 数据表协同工作。
一言以蔽之,plotly是一款擅长交互的Python绘图库,下面就初步使用一下这个库的三维绘图功能。此前曾经用matplotlib画了正二十面体和足球:Python绘制正二十面体;画足球,这次用plotly复现一下正二十面体的绘制过程,也体验一下这两个绘图包的差异。
来绘制一个正二十面体。
顶点
正20面体的12个顶点刚好可以分为三组,每一组都是一个符合黄金分割比例的长方形,而且这三个长方形是互相正交的。
所以,想绘制一个正二十面体是比较容易的
import plotly
import plotly.express as px
import numpy as np
from itertools import product
G = (np.sqrt(5)-1)/2
def getVertex():
pt2 = [(a,b) for a,b in product([1,-1], [G, -G])]
pts = [(a,b,0) for a,b in pt2]
pts += [(0,a,b) for a,b in pt2]
pts += [(b,0,a) for a,b in pt2]
return np.array(pts)
xs, ys, zs = getVertex().T
fig = px.scatter_3d(x=xs, y=ys, z=zs,
size=np.ones_like(xs)*0.5)
fig.show()
得到顶点

棱
接下来连接这12个顶点,由于点数较少,所以直接遍历也不至于运算量爆炸。另一方面,正二十面体边长相同,而这些相同的边连接的也必然是最近的点,所以接下来只需建立顶点之间的距离矩阵,并抽取出距离最短的线。
def getDisMat(pts):
N = len(pts)
dMat = np.ones([N,N])*np.inf
for i in range(N):
for j in range(i):
dMat[i,j] = np.linalg.norm([pts[i]-pts[j]])
return dMat
pts = getVertex()
dMat = getDisMat(pts)
# 由于存在舍入误差,所以得到的边的数值可能不唯一
ix, jx = np.where((dMat-np.min(dMat))<0.01)
接下来,绘制正二十面体的棱
edges = []
for k in range(len(ix)):
edges.append(pts[ix[k]].tolist() + [k])
edges.append(pts[jx[k]].tolist() + [k])
edges = np.array(edges)
fig = px.line_3d(edges, x=0, y=1, z=2, color=3)
fig.show()
效果如图所示

实现正二十面体
接下来要对面上色。由于三棱成个面,所以只需得到所有三条棱的组合,只要这三条棱可以组成三角形,就能获取所有的三角面。当然,这一切的前提是,正二十面体只有30个棱,即使遍历多次,也无非27k的计算量,是完全没问题的。
def isFace(e1, e2, e3):
pts = np.vstack([e1, e2, e3])
pts = np.unique(pts, axis=0)
return len(pts)==3
edges = [pts[[i,j]] for i,j in zip(ix, jx)]
from itertools import combinations
faces = [es for es in combinations(edges, 3)
if isFace(*es)]
最后得到的faces有20个元素,每个元素由3条棱组成,每条棱有两个顶点,故而可以缩减为三个顶点。
ptFace = [np.unique(np.vstack(f),axis=0) for f in faces]
ptFace = np.vstack(ptFace)
接下来绘制一下,plotly绘制三角面的逻辑是,除了需要指定三角面的三个坐标之外,还需指定三角面的顶点序号
import plotly.figure_factory as ff
simplices = np.arange(len(ptFace)).reshape(-1,3)
fig = ff.create_trisurf(x=ptFace[:,0],
y=ptFace[:,1], z=ptFace[:,2],
simplices=simplices)
fig.show()
效果如下