If every unfolding we experience takes us further along in life, then, we are truly experiencing what life is offering.
如果我们在人生中体验的每一次转变都让我们在生活中走得更远,那么,我们就真正的体验到了生活想让我们体验的东西。
Do not try and bend the spoon. That's impossible. Instead, only try to realize the truth. There is no spoon. Then you'll see that it is not the spoon that bends. It is only yourself.
不要试图弯曲汤匙。那是不可能的。你只能试着去理解一件事实。汤匙不存在。你会发现被弯曲的不是汤匙。那只是你自己。
目录:
一.题目(最短路径)
1.关于动态规划
二.三种思路
1.思路一(深搜)
2.思路二(动态规划)
3.思路三(数论方法)
总结
三.题目(最短路径和)
一.题目(最短路径)
1.关于动态规划
动态规划算法的基本思想是:将待求解的问题分解成若干个相互联系的子问题,先求解子问题,然后从这些子问题的解得到原问题的解;对于重复出现的子问题,只在第一次遇到的时候对它进行求解,并把答案保存起来,让以后再次遇到时直接引用答案,不必重新求解。动态规划算法将问题的解决方案视为一系列决策的结果。
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为Finish)。
问总共有多少条不同的路径?

输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 2, n = 3
输出:3
解释: 从左上角开始,总共有 3 条路径可以到达右下角。
向右 -> 向右 -> 向下
向右 -> 向下 -> 向右
向下 -> 向右 -> 向右
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9
二.三种思路
思路一(深搜)
这道题目,刚一看最直观的想法就是用图论里的深搜,来枚举出来有多少种路径。
注意题目中说机器人每次只能向下或者向右移动一步,那么其实机器人走过的路径可以抽象为一棵二叉树,而叶子节点就是终点!
如图举例:

此时问题就可以转化为求二叉树叶子节点的个数,代码如下:
class Solution {
private:
int dfs(int i, int j, int m, int n) {
if (i > m || j > n) return 0; // 越界了
if (i == m && j == n) return 1; // 找到一种方法,相当于找到了叶子节点
return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);
}
public:
int uniquePaths(int m, int n) {
return dfs(1, 1, m, n);
}
};大家如果提交了代码就会发现超时了!
来分析一下时间复杂度,这个深搜的算法,其实就是要遍历整个二叉树。
这棵树的深度其实就是m+n-1(深度按从1开始计算)。
那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树(其实没有遍历整个满二叉树,只是近似而已)
所以上面深搜代码的时间复杂度为O(2^(m + n - 1) - 1),可以看出,这是指数级别的时间复杂度,是非常大的。
2.思路二(动态规划)
机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。
按照动规五部曲来分析:
1)确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
2)确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。
此时在回顾一下 dp[i - 1][j] 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dp[i][j - 1]同理。
那么很自然,dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。
3)dp数组的初始化
如何初始化呢,首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
所以初始化代码为:
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;4)确定遍历顺序
这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
这样就可以保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。
5)举例推导dp数组
如图所示:

以上动规五部曲分析完毕,C++代码如下:
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};时间复杂度:O(m × n)
空间复杂度:O(m × n)
3.思路三(数论方法)
在这个图中,可以看出一共m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。

在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
那么有几种走法呢? 可以转化为,给你m + n - 2个不同的数,随便取m - 1个数,有几种取法。
那么这就是一个组合问题了。
那么答案,如图所示:

求组合的时候,要防止两个int相乘溢出! 所以不能把算式的分子都算出来,分母都算出来再做除法。
例如如下代码是不行的。
class Solution {
public:
int uniquePaths(int m, int n) {
int numerator = 1, denominator = 1;
int count = m - 1;
int t = m + n - 2;
while (count--) numerator *= (t--); // 计算分子,此时分子就会溢出
for (int i = 1; i <= m - 1; i++) denominator *= i; // 计算分母
return numerator / denominator;
}
};需要在计算分子的时候,不断除以分母,代码如下:
class Solution {
public:
int uniquePaths(int m, int n) {
long long numerator = 1; // 分子
int denominator = m - 1; // 分母
int count = m - 1;
int t = m + n - 2;
while (count--) {
numerator *= (t--);
while (denominator != 0 && numerator % denominator == 0) {
numerator /= denominator;
denominator--;
}
}
return numerator;
}
};时间复杂度:O(m)
空间复杂度:O(1)
计算组合问题的代码还是有难度的,特别是处理溢出的情况!
总结
本文分别给出了深搜,动规,数论三种方法。
深搜当然是超时了,顺便分析了一下使用深搜的时间复杂度,就可以看出为什么超时了。然后在给出动规的方法,依然是使用动规五部曲,这次我们就要考虑如何正确的初始化了,初始化和遍历顺序其实也很重要!
三.题目(最短路径和)
给定一个 n * m 的矩阵 a,从左上角开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,输出所有的路径中最小的路径和。
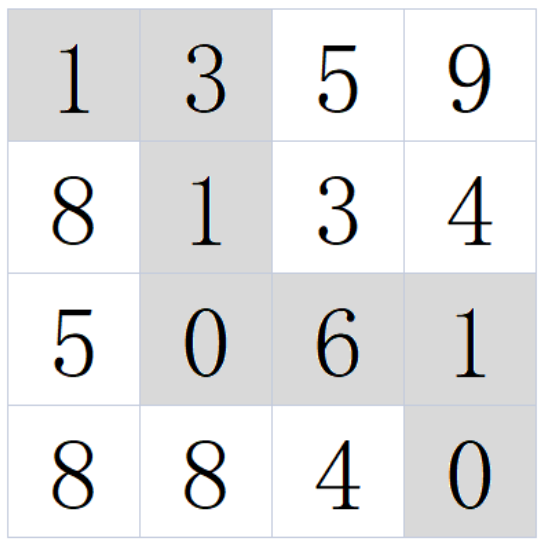
例如:当输入[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]时,对应的返回值为12,
所选择的最小累加和路径如下图所示:

1.思路
最朴素的解法莫过于枚举所有的路径,然后求和,找出其中最大值。但是像这种有状态值可以转移的问题,我们可以尝试用动态规划。
具体做法:
step 1:我们可以构造一个与矩阵同样大小的二维辅助数组,其中]dp[i][j]表示以(i,j)位置为终点的最短路径和,则dp[0][0]=matrix[0][0]。
step 2:很容易知道第一行与第一列,只能分别向右或向下,没有第二种选择,因此第一行只能由其左边的累加,第一列只能由其上面的累加。
step 3:边缘状态构造好以后,遍历矩阵,补全矩阵中每个位置的dp数组值:如果当前的位置是(i,j),上一步要么是(i−1,j)往下,要么就是(i,j−1)往右,那么取其中较小值与当前位置的值相加就是到当前位置的最小路径和,因此状态转移公式为dp[i][j]=min(dp[i−1][j],dp[i][j−1])+matrix[i][j]。
step 4:最后移动到(n−1,m−1)的位置就是到右下角的最短路径和。
2.代码实现
class Solution {
public:
int minPathSum(vector<vector<int> >& matrix) {
// write code here
int m=matrix.size();
int n=matrix[0].size();
vector<vector<int>>dp(m,vector<int>(n,0));
dp[0][0]=matrix[0][0];
for(int i=1;i<m;i++)
{
dp[i][0]=dp[i-1][0]+matrix[i][0];
}
for(int j=1;j<n;j++)
{
dp[0][j]=dp[0][j-1]+matrix[0][j];
}
for(int i=1;i<m;i++)
{
for(int j=0;j<n;j++)
{
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+matrix[i][j];
}
}
return dp[m-1][n-1];
}
};这是两道经典的dp题目,值得反反复思琢磨。
2023.02.23
From:努力进大厂的新青年