目录
零:移步
一.修炼必备
二.问题思考
三.整型在内存中的存储
三.大端字节序和小端字节序
四.浮点数在内存中的存储
零:移步
CSDN由于我的排版不怎么好看,我的有道云笔记相当的美观,请移步至有道云笔记
一.修炼必备
1.入门必备:VS2019社区版,下载地址:Visual Studio 较旧的下载 - 2019、2017、2015 和以前的版本 (microsoft.com)
2.趁手武器:印象笔记/有道云笔记
3.修炼秘籍:牛客网 - 找工作神器|笔试题库|面试经验|实习招聘内推,求职就业一站解决_牛客网 (nowcoder.com)
4.雷劫必备:leetcode 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
注:遇到瓶颈怎么办?百度百科_全球领先的中文百科全书 (baidu.com)
二.问题思考
1.C语言数据的类型?
2.整数在计算机中二进制的表示形式有几种?正整数和负整数相同的吗?
3.整数在内存中的存放的是什么?怎么验证是这样存放的?
4.为什么计算机中存放的是补码?
5.什么是字节序?
6.数据的字节序是在内存中怎么存储的?
7.如何判断一个数据的字节序是大端字节序还是小端字节序?
8.浮点数在内存中的存储和整数的存储是一样的吗?
9.浮点数的存储规则
三.整型在内存中的存储
1.C语言数据的类型?
1)整型:char,short,int,long,long long
2)浮点型:float,double
3)构造类型:struct,union
4)指针类型:int*,char*,double*等
5)空类型:void(常用于函数的返回类型,指针类型,函数的参数)
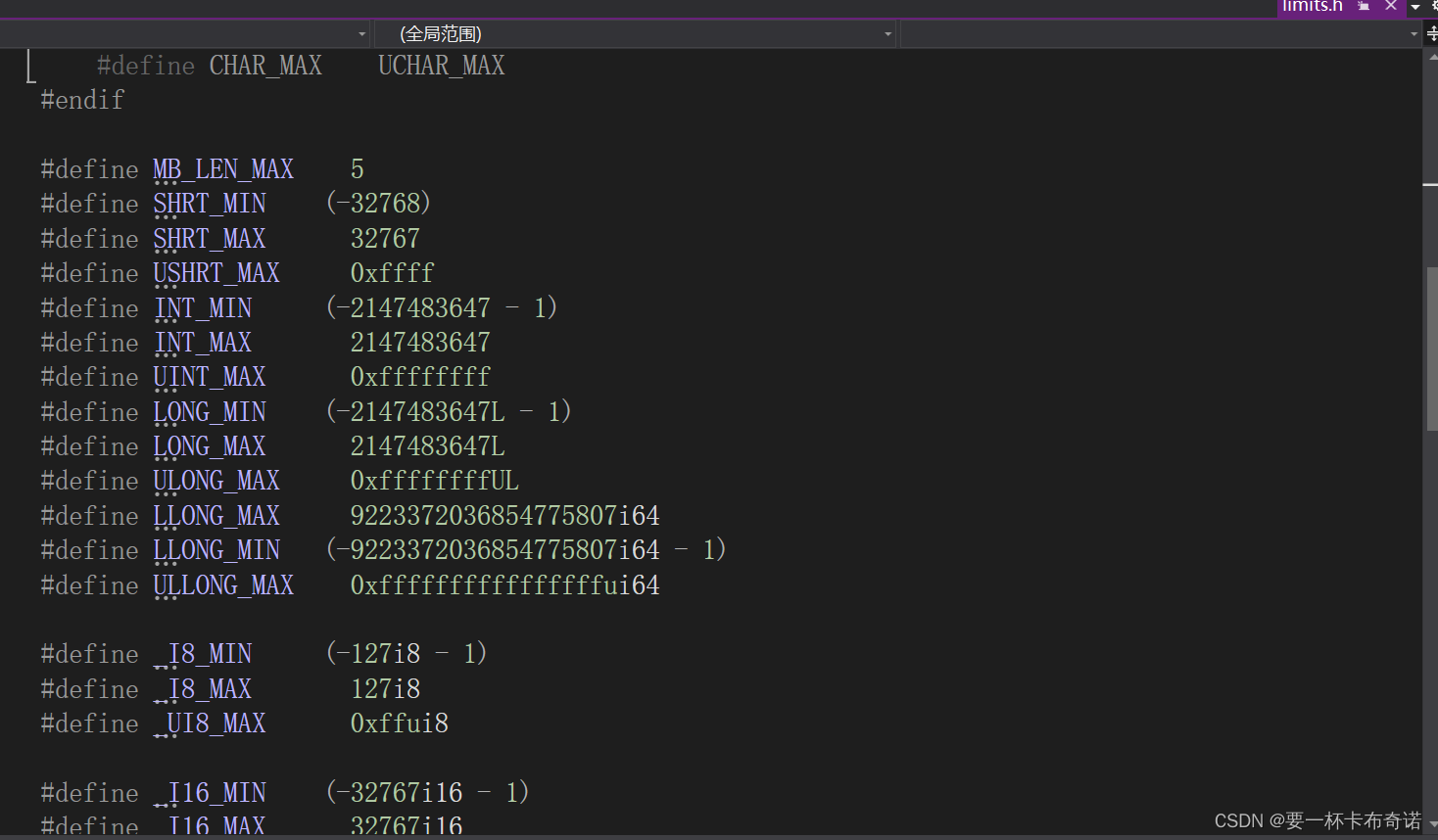
2.如何查看整数类型的值范围?
——在limits.h头文件中查看
3.整数在计算机中二进制的表示形式有几种?正整数和负整数相同的吗?
1)整数在计算机中的表示形式有:原码、反码、补码
2)正整数的原码、反码、补码均相同
3)负整数的原码、反码、补码的规则
原码:把整数直接按照二进制进行转化
反码:原码的符号位不变,其他位按位取反
补码:反码 + 1
#include <stdio.h>
//原码、反码、补码的转化规则
int main()
{
//正整数的原码、反码、补码相同
int num1 = 5;
//00000000 00000000 00000000 00000101 num1的补码
//负整数的原码、反码、补码转化
int num2 = -5;
//10000000 00000000 00000000 00000101 原码
//(原码符号位不变,其他位取反)
//11111111 11111111 11111111 11111010 反码
//(反码+1)
//11111111 11111111 11111111 11111011 补码
return 0;
}4.如何证明整型在内存中存储的是补码?
——使用负数证明
1)打印出负数的十六进制形式(十六进制是无符号的打印)
#include <stdio.h>
//证明整型在内存中存储的是补码
int main()
{
int num1 = 1;
//00000000 00000000 00000000 00000001 1的补码
int num2 = -1;
//11111111 11111111 11111111 11111111 -1的补码
//注:每四个2进制位可以组成一个十六进制:ffffff
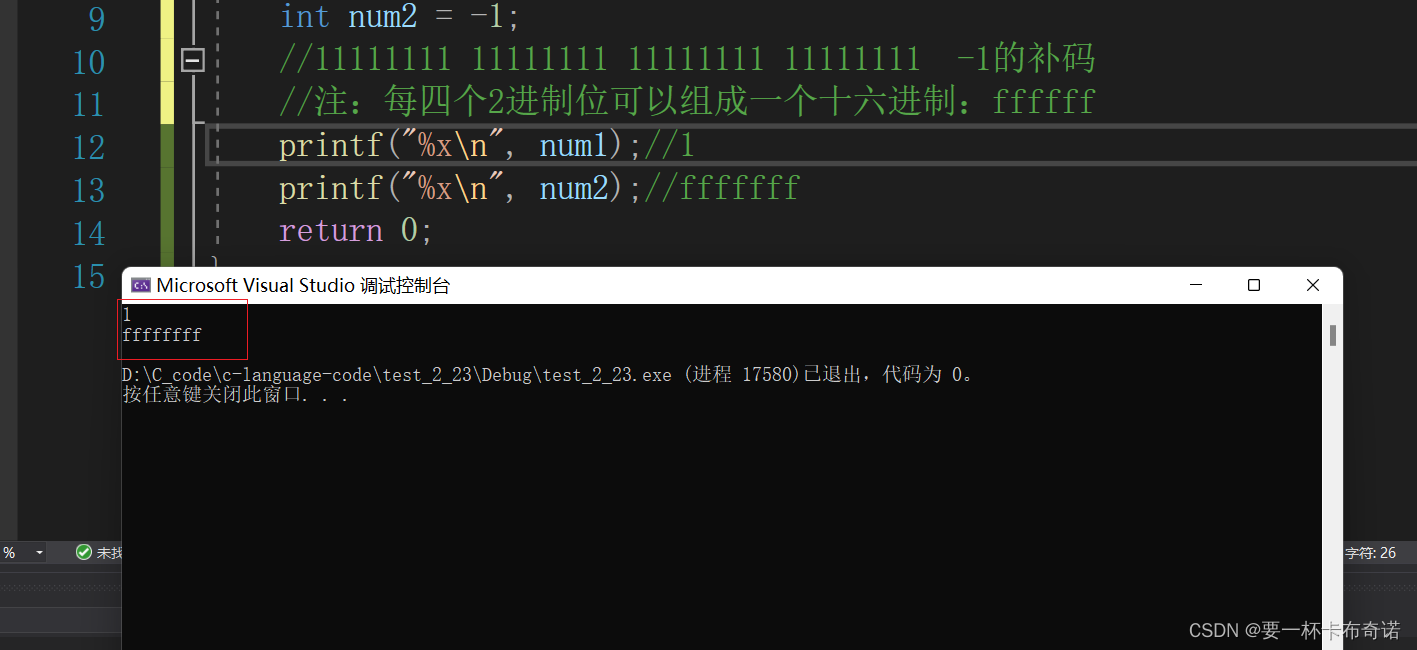
printf("%x\n", num1);//1
printf("%x\n", num2);//fffffff
return 0;
}运行结果如图:
2)调试查看负数在内存中的存储形式
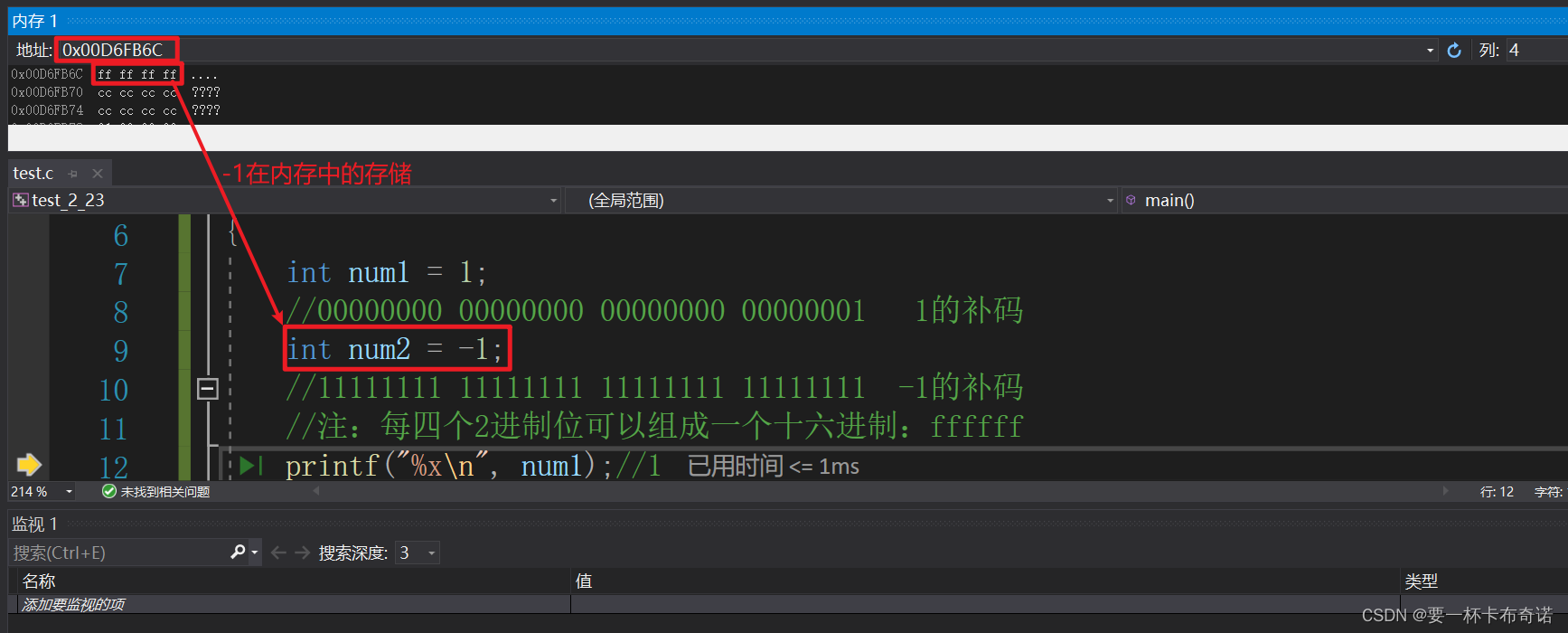
5.为什么计算机中存放的是补码?
1)方便运算:省去了计算机判断符号位或判断+/-运算的麻烦,采用补码后,不管是加法还是减法均是使用加法进行运算(CPU只有加法器)
2)更加标准:保证了系统的编码的一致性和连续性,也同时避免了+/-0的麻烦
6.practice
case 1:思考并分析
#include <stdio.h>
int main()
{
char a = -1;
//默认是有符号数
//10000001 原码
//11111110 反码
//11111111 补码
//11111111 11111111 11111111 11111111 整型提升
//11111111 截取(补码)
//10000001 原码(-1)
signed char b = -1;
//b 和 a一样
unsigned char c = -1;
//10000001 原码
//11111110 反码
//11111111 补码
//11111111 11111111 11111111 11111111 整型提升
//11111111 截取 --无符号数:255
printf("a=%d,b=%d,c=%d\n", a, b, c);//-1 -1,255
return 0;
}运行结果如图:
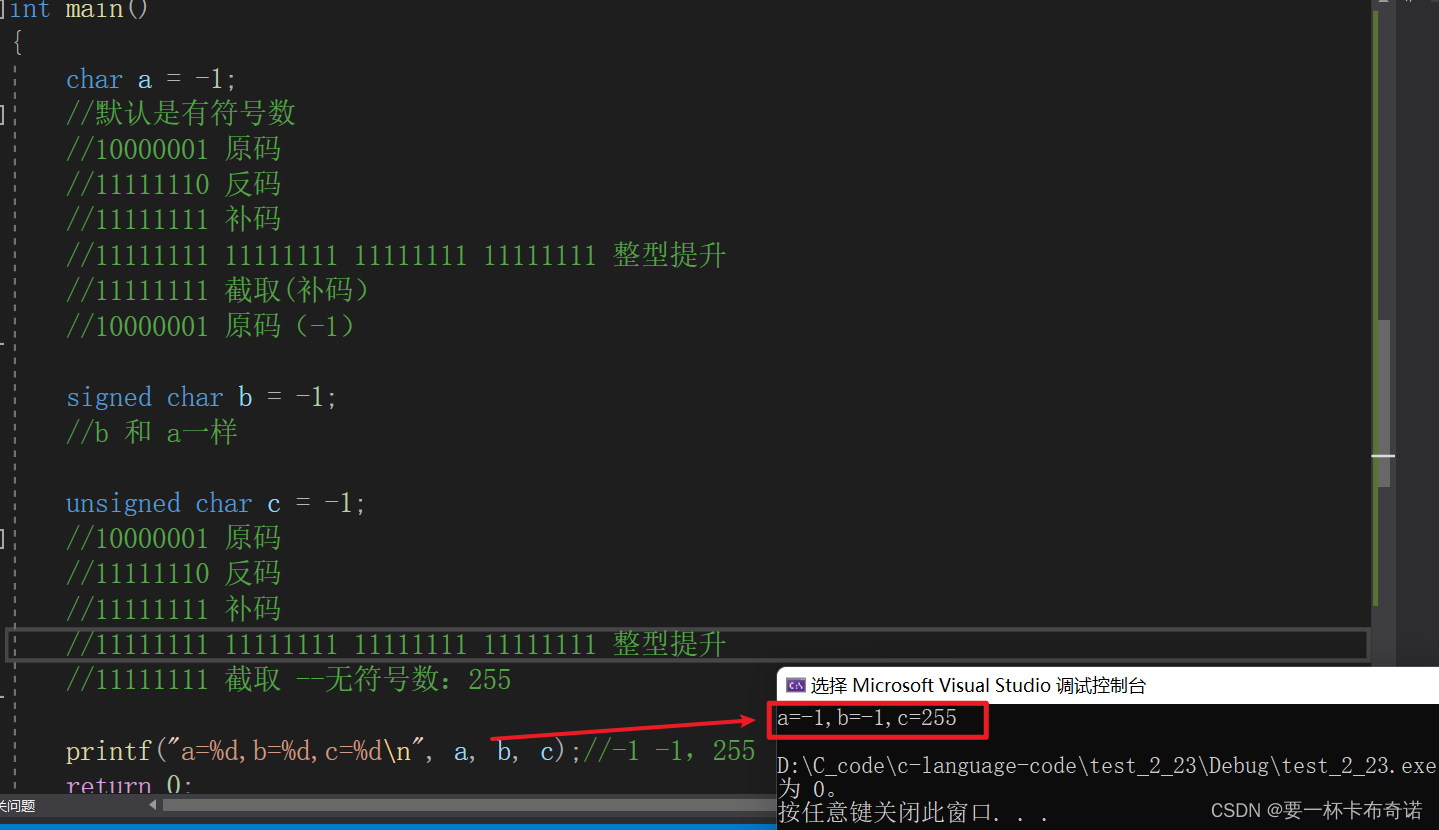
case 2:思考并分析
#include <stdio.h>
int main()
{
char a = -128;
//10000000 -- 补码
//因为是无符号整型打印,需要整型提升
//11111111 11111111 11111111 10000000 -- 4294967168(结果)
printf("%u\n", a);//4294967168
return 0;
}运行结果如图:
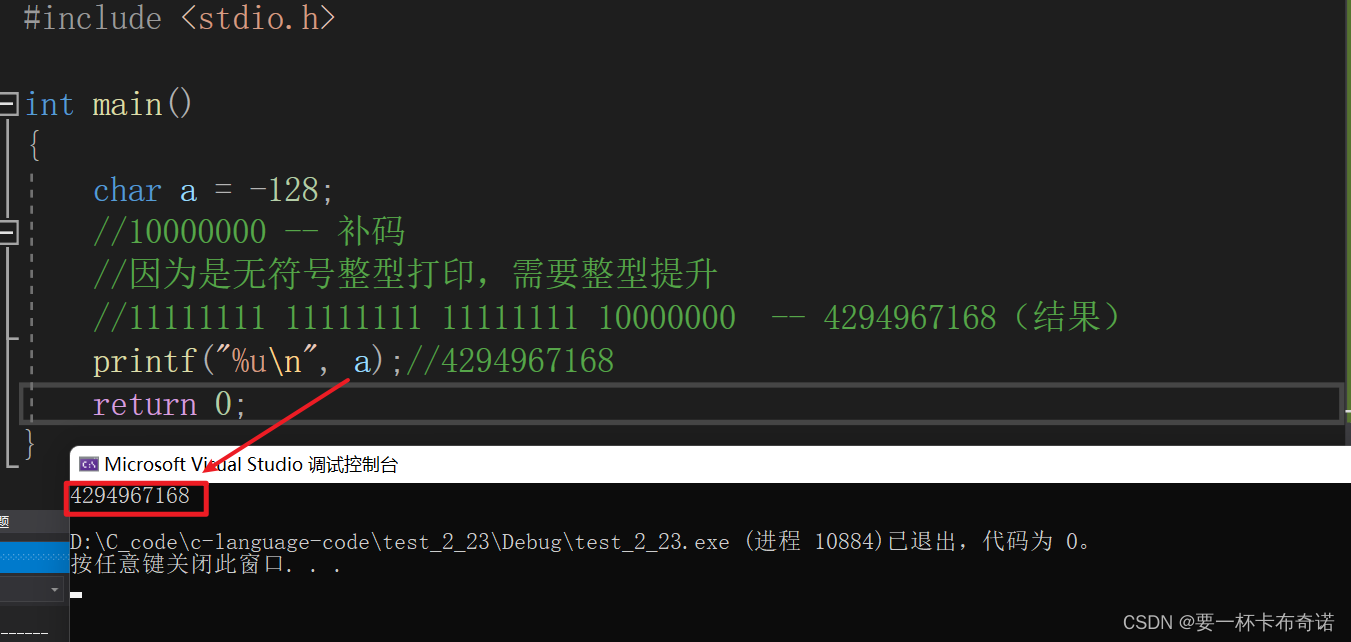
case 3:思考并分析
#include <stdio.h>
int main()
{
char a = 128;
//10000000
//11111111 11111111 11111111 10000000 整型提升
//-- 4294967168(结果)
printf("%u\n", a);//4294967168
return 0;
}运行结果如图:
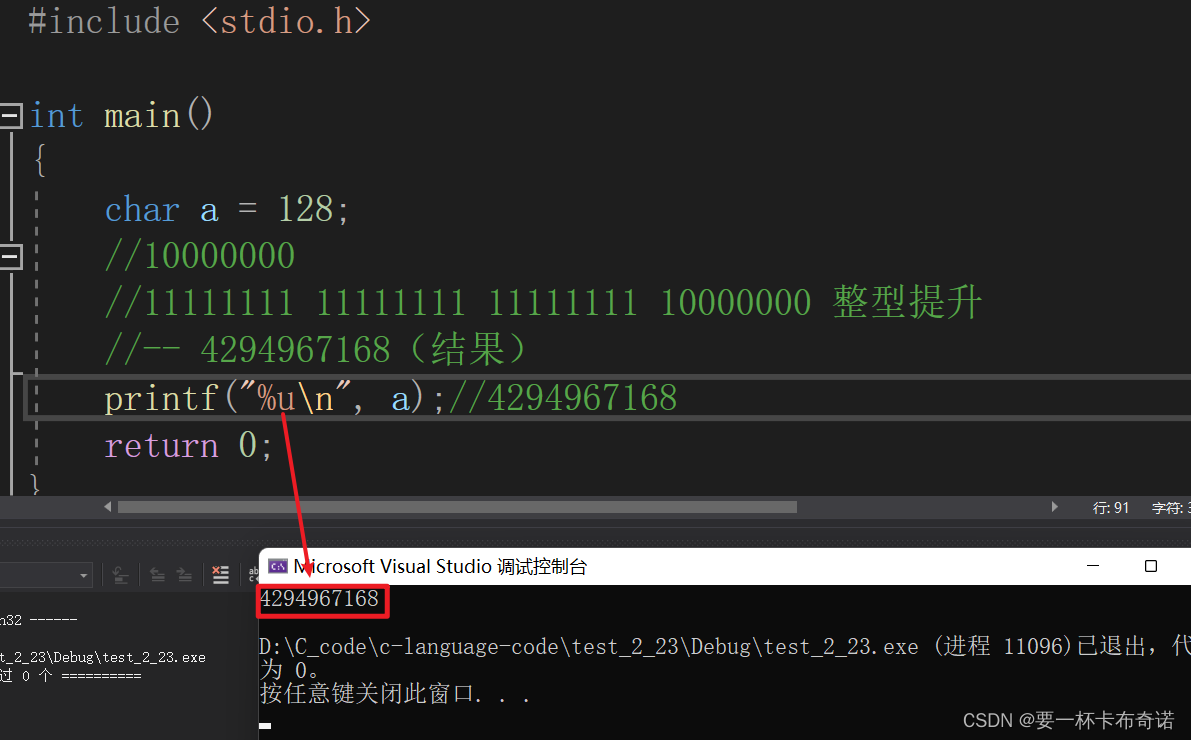
case 4:思考并分析
#include <stdio.h>
int main()
{
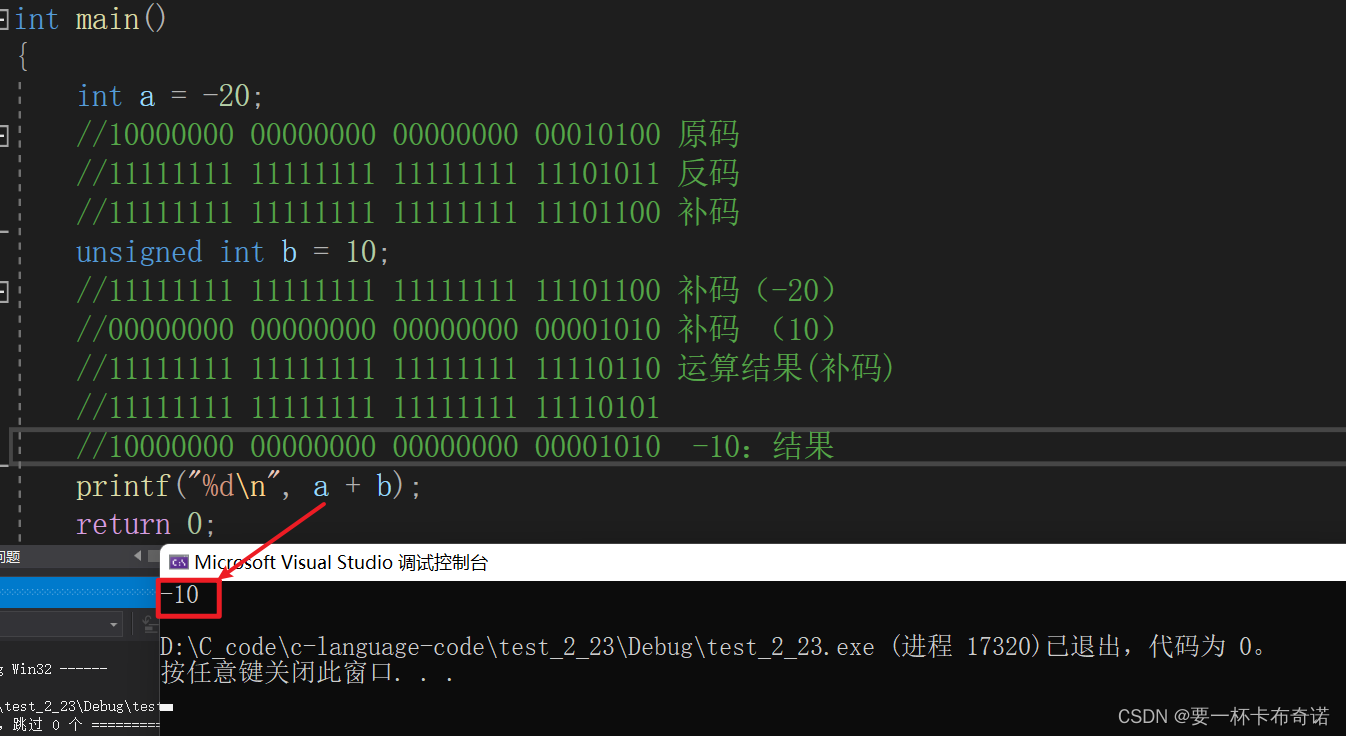
int a = -20;
//10000000 00000000 00000000 00010100 原码
//11111111 11111111 11111111 11101011 反码
//11111111 11111111 11111111 11101100 补码
unsigned int b = 10;
//11111111 11111111 11111111 11101100 补码(-20)
//00000000 00000000 00000000 00001010 补码 (10)
//11111111 11111111 11111111 11110110 运算结果(补码)
//11111111 11111111 11111111 11110101
//10000000 00000000 00000000 00001010 -10:结果
printf("%d\n", a + b);
return 0;
}运行结果如图:
case 5:思考并分析
#include <stdio.h>
int main()
{
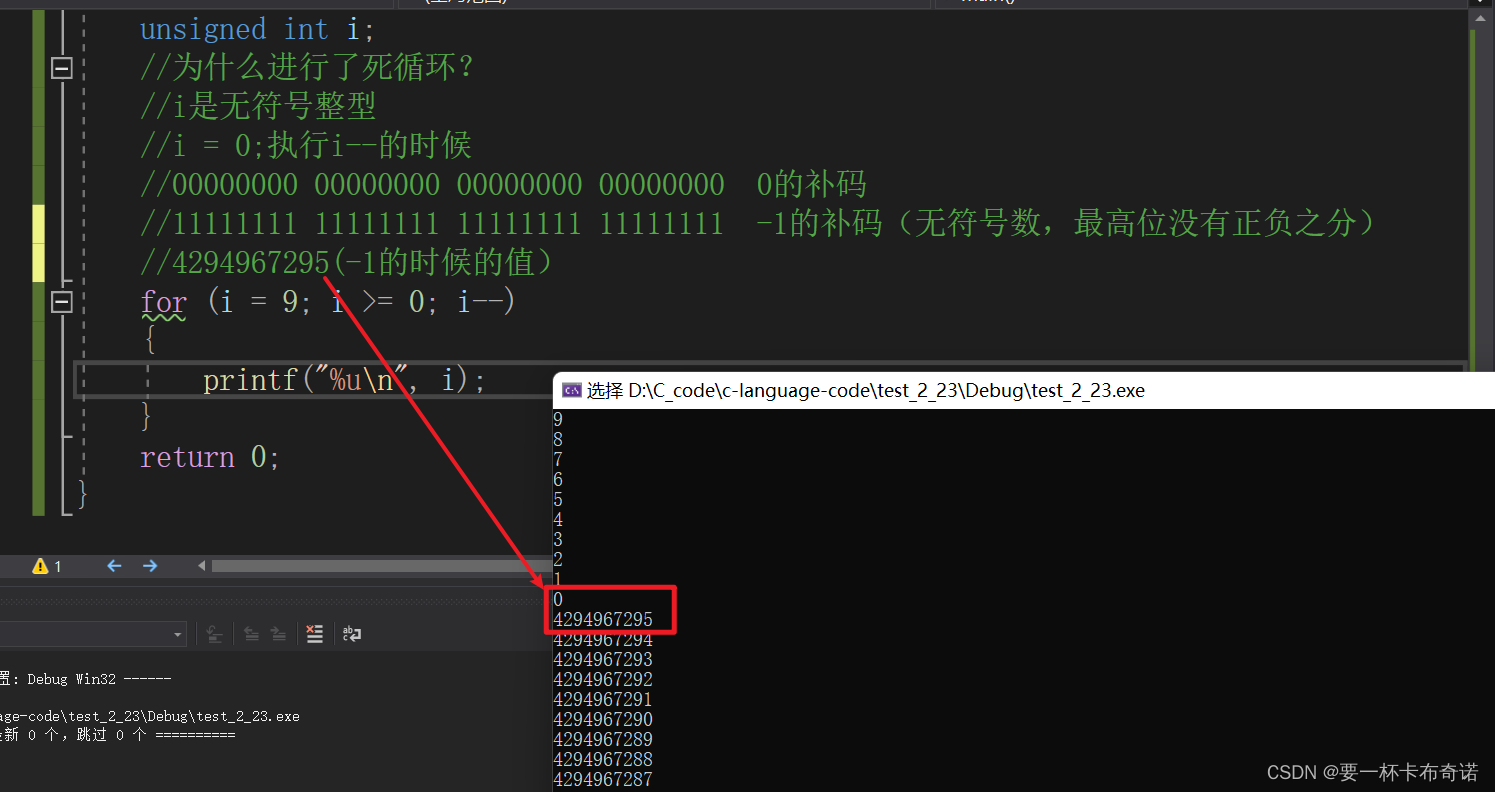
unsigned int i;
//为什么进行了死循环?
//i是无符号整型
//i = 0;执行i--的时候
//00000000 00000000 00000000 00000000 0的补码
//11111111 11111111 11111111 11111111 -1的补码(无符号数,最高位没有正负之分)
//4294967295(-1的时候的值)
for (i = 9; i >= 0; i--)
{
printf("%u\n", i);
}
return 0;
}运行结果如图:
case 6:思考并分析
#include <stdio.h>
#include <string.h>
int main()
{
char a[1000];
int i;
for (i = 0; i < 1000; i++)
{
a[i] = -1 - i;
//11111111 -1的补码
//11111110 -2的补码
//11111101 -3的补码
//……
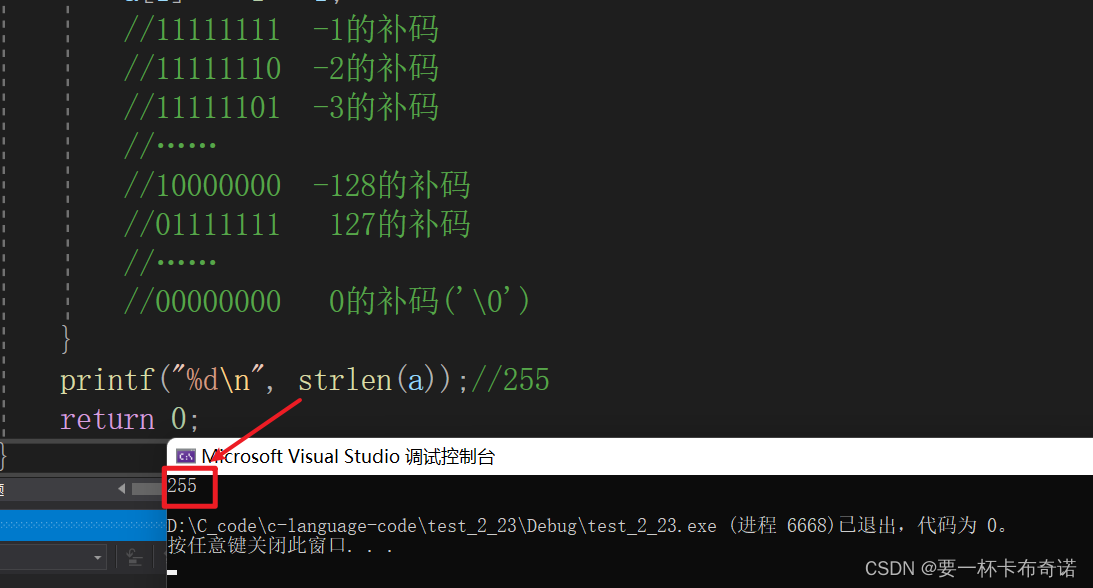
//10000000 -128的补码
//01111111 127的补码
//……
//00000000 0的补码('\0')
}
printf("%d\n", strlen(a));//255
return 0;
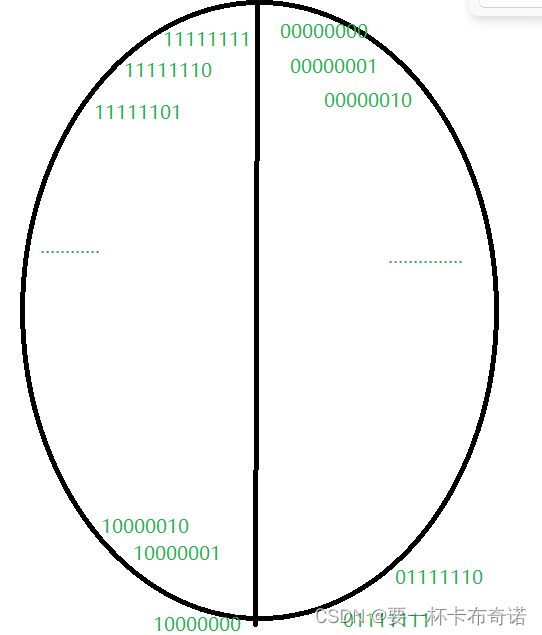
}一图了解char的范围:
运行结果如图:
 case 7:思考并分析
case 7:思考并分析
#include <stdio.h>
unsigned char i;
int main()
{
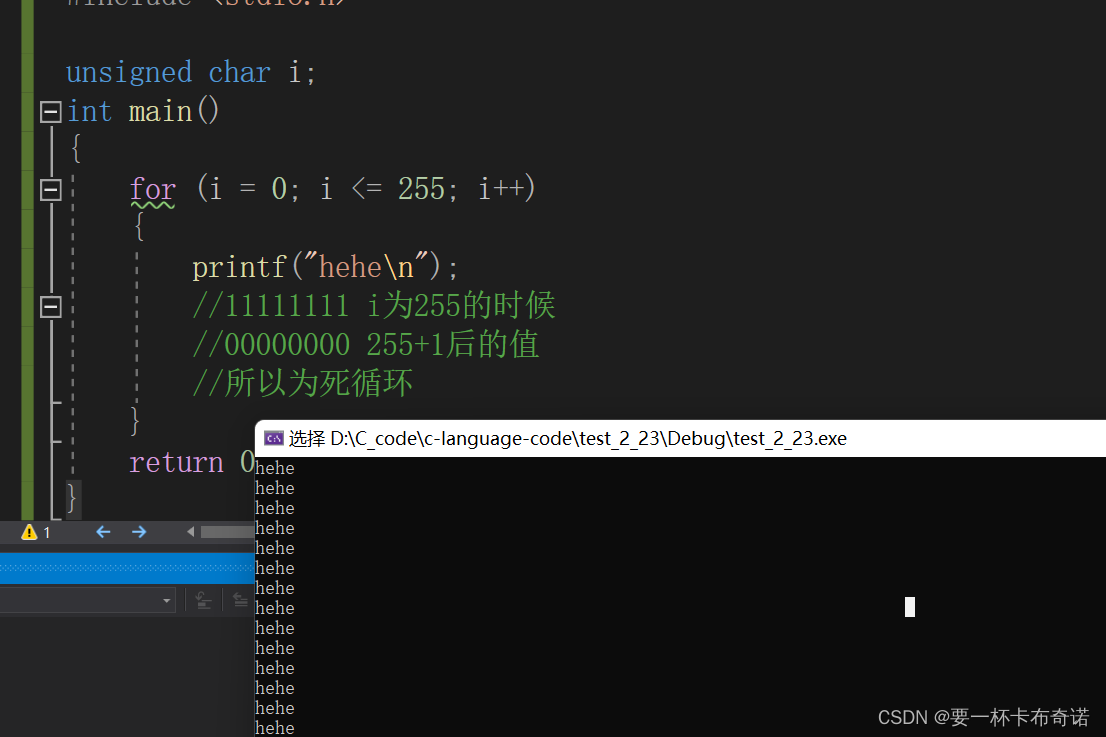
for (i = 0; i <= 255; i++)
{
printf("hehe\n");
//11111111 i为255的时候
//00000000 255+1后的值
//所以为死循环
}
return 0;
}运行结果如图:
三.大端字节序和小端字节序
1.什么是字节序?
——字节序又称为端序或尾序,指计算机内存中多字节数据在内存中的排列顺序
2.数据的字节序是在内存中怎么存储的?
——浮点数和整数的字节序都有大端和小端两种字节序
1)小端字节序
——数据的低位字节存储在内存的低地址处,高位字节存储在内存的高地址处
2)大端字节序
——数据的低位字节存储在内存的高地址处,高位字节存储在内存的低地址处
3.如何判断一个数据的字节序是大端字节序还是小端字节序?
——内存中查看该数据的存储形式,看低位存放在内存中的位置
图解:
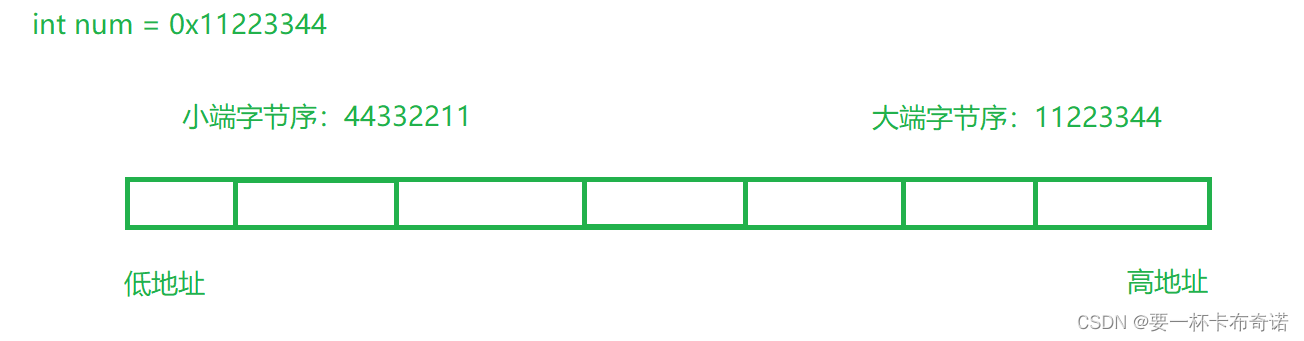
代码解释:
#include <stdio.h>
int main()
{
int num = 0x11223344;
float data = 5.5;
//101.1
//01000000101100000000000000000000
//40b00000:十六进制形式
return 0;
}小端字节序在内存中的图解:
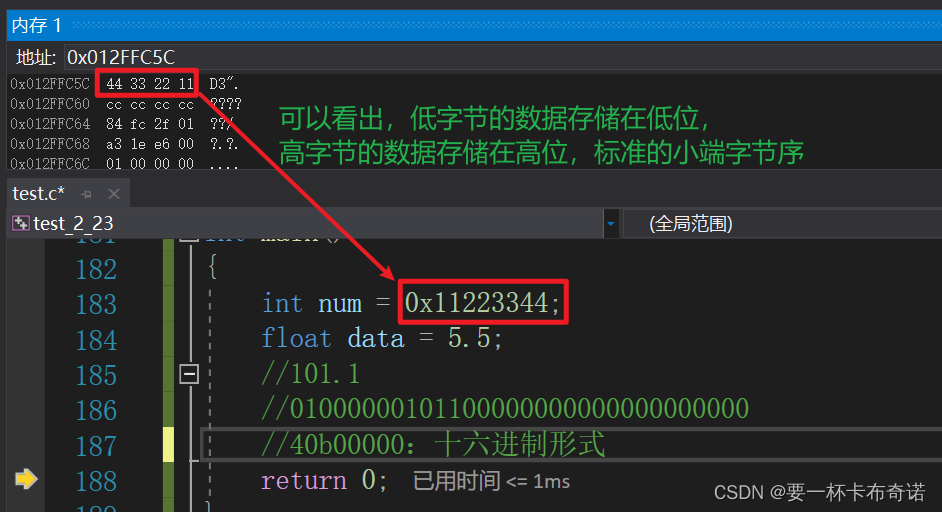
大端字节序在内存中的图解:
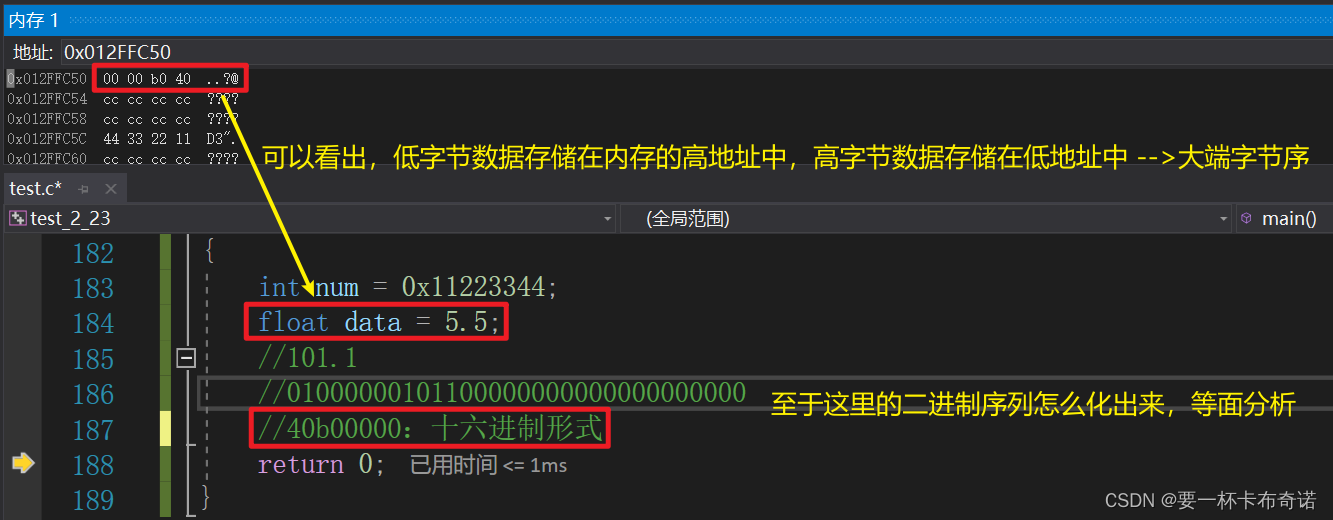
4.一道笔试题加强巩固
——请判断一个机器是大端字节序还是小端字节序
思路分析:我们只需要判断取出1的最低位即可,如果是0,则是大端存储序列,如果是1,则是小端字节序
#include <stdio.h>
//判断当前机器是大端还是小端字节序
int main()
{
int a = 1;
char* p = (char*)&a;
if (*p == 1)
{
printf("小端字节序\n");
}
else
{
printf("大端字节序\n");
}
return 0;
}代码是写出来了,但是这样写是不是有点太low了,我们换种方式
#include <stdio.h>
//判断当前机器是大端还是小端字节序
int judge(int a)
{
char* p = (char*)&a;
return *p;//如果小端,直接返回1,大端返回0
}
int main()
{
int a = 1;
if (judge(a) == 1)
{
printf("小端字节序\n");
}
else
{
printf("大端字节序\n");
}
return 0;
}运行结果如图:
四.浮点数在内存中的存储
1.怎么查看浮点数的值范围?
——在float.h头文件中查看
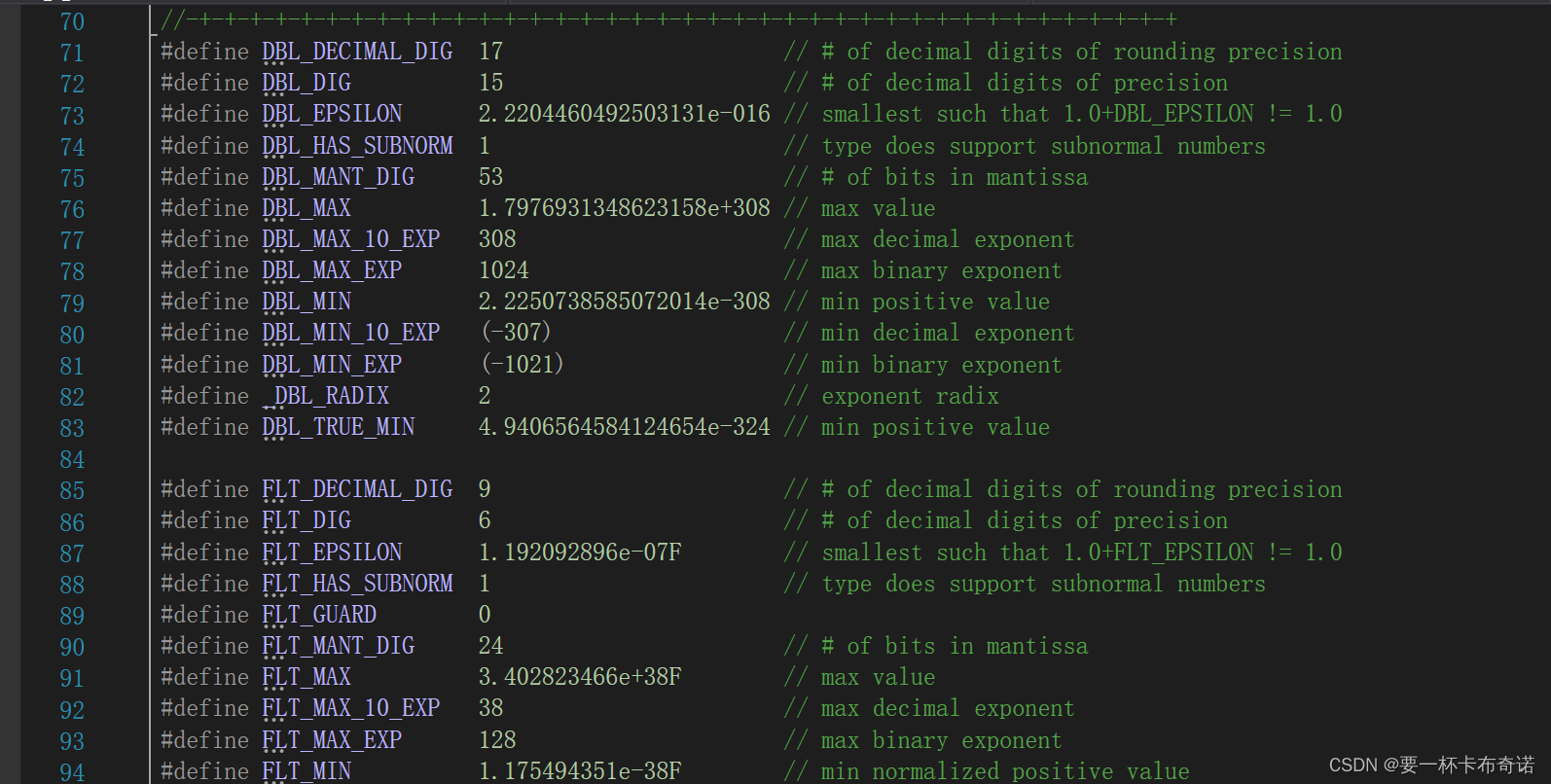
2.浮点数的存储规则
1)浮点数进行存储的形式:(-1)^S * M * 2^E;
——解释:S表示符号位,M表示有效数字:1
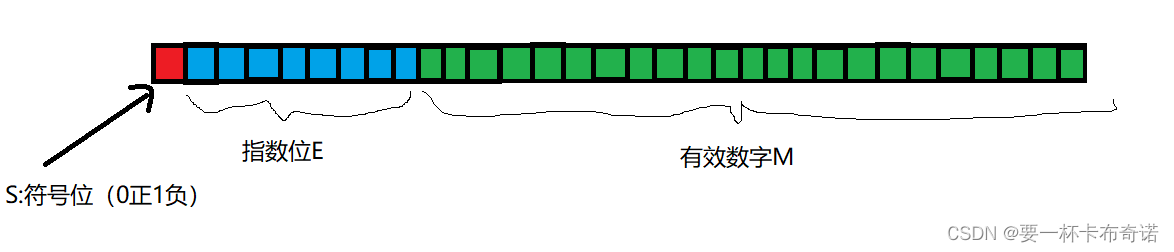
2)在IEEE的规定下,最高位的1位S表示符号位,接下来的八位表示指数E,剩下的23位表示有效数字M
float图解:
double图解:
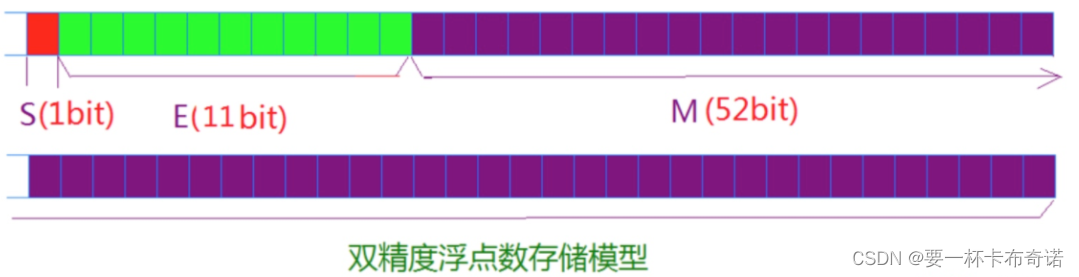
3)由图知:float的指数位有8位,double的指数位有11位,float的M有23位,double的M有52位
4)IEEE对M和E还有一些特别的规定
i.因为1
ii.指数E是一个无符号整数(unsigned int)
a.float的话,E的值在0~255之间;double的话,E的值在0~2047之间
b.注意,科学计数法中的E是可以是为负数的,所以我们在计算E的时候,应该加上一个中间值,float类型+127,double类型+1023
iii.E从内存中取出的三种情况
a.E不为全0或全1
——使用E转化的十进制值减去127/1023得到真实值,在给有效数字加上小数点前面的1(常用)
b.E全为0
——E的值是1-127或1-1023,得到真实值,这个时候我们不需要在加上小数点前面的1了,这样做是为了表示正负0,以及接近0的很小的数值
c.E全为1
——这时,如果有效数字全为0,表示±无穷大(正负取决于符号位s)
3.practice
case 1:分析解释下面代码
#include <stdio.h>
int main()
{
int num = 9;
float* p = (float*)#
printf("%d\n", num);//9
printf("%f\n", *p);//0.000000
//分析为什么是0.000000
//00000000 00000000 00000000 00001001 9的补码
//浮点数中看到的形式
//0 00000000 00000000000000000001001
//相当于0.00000000000000000001001 * (1 - 2^-126)
//这个数非常小,而浮点数默认取小数点后6位,所以为0.000000
*p = 9.0;
//1001.0
//1.001 * 2^3
//S = 0,E = 2, M = 1.001
//可以写出*p的的二进制序列
//0 10000010 00100000000000000000000 *p的二进制序列
//化为整数:1091567616
printf("%d\n", num);//1091567616
printf("%f\n", *p);//9.000000
return 0;
}运行结果如图:
case 2:分析并解释
#include <stdio.h>
int main()
{
float num = 5.5;
//101.1 --> 1.011
//S = 0,E = 2, M = 1.011 --> 得出二进制序列
//0 10000001 01100000000000000000000 num的二进制序列
int* p = (int*)#
//01000000101100000000000000000000 结果:1085276160
printf("%f\n", num);//5.500000
printf("%d\n", *p);//1085276160
*p = 5;
//01000000 10110000 00000000 00000000序列变为:
//00000000 00000000 00000000 00000101 5
//转化为float类型
//0 00000000 00000000000000000000101
//结果:0.00000000000000000000101 * 2 ^ (-126);(极小的数)
//转为float即为0.000000
printf("%f\n", num);//0.000000
printf("%d\n", *p);//5
return 0;
}运行结果如图:
!!!恭喜你,突破至筑基七层!!!