文章目录
- 一、电磁场的基本规律
- 二、静态电磁场及其边值问题的解
- 三、分离变量法
- 四、均匀平面波的反射与透射
- 五、时变电磁场与均匀平面波在无界空间中的传播
- 六、导行电磁波
- 七、电磁辐射
- 往年真题回忆
- 复习建议
一、电磁场的基本规律
设在 x < 0 x<0 x<0 处为真空, x > 0 x > 0 x>0 区域中充满介电常数为 ε \varepsilon ε 的均匀介质,而平面 x = 0 x = 0 x=0 均匀带电,面电荷密度为 ρ 0 \rho_0 ρ0 。已知在 x < 0 x<0 x<0 处,电场为 E 1 → = e x → a + e y → b + e z → c \overrightarrow{E_{1}}=\overrightarrow{e_{x}} a+\overrightarrow{e_{y}} b+\overrightarrow{e_{z}} c E1=exa+eyb+ezc ,试求 x > 0 x > 0 x>0 区域内的电场能量密度。
二、静态电磁场及其边值问题的解
一圆形截面的无限长直铜线,通过电流为I,在铜线外套上一个磁导率为
μ
\mu
μ 的磁性材料制成的圆筒,与之同轴,圆筒的内外半径分别为
r
1
r_1
r1 及
r
2
r_2
r2 (
r
1
r_1
r1 <
r
2
r_2
r2 )。求:
(1)圆筒中的磁感应强度
B
⃗
\vec{B}
B;
(2)圆筒内的磁化强度
M
⃗
\vec{M}
M ;
(3)圆筒内的磁化电流体密度
J
m
→
\overrightarrow{J_m}
Jm 和圆筒内外表面的磁化电流面密度
J
m
s
→
\overrightarrow{J_{ms}}
Jms
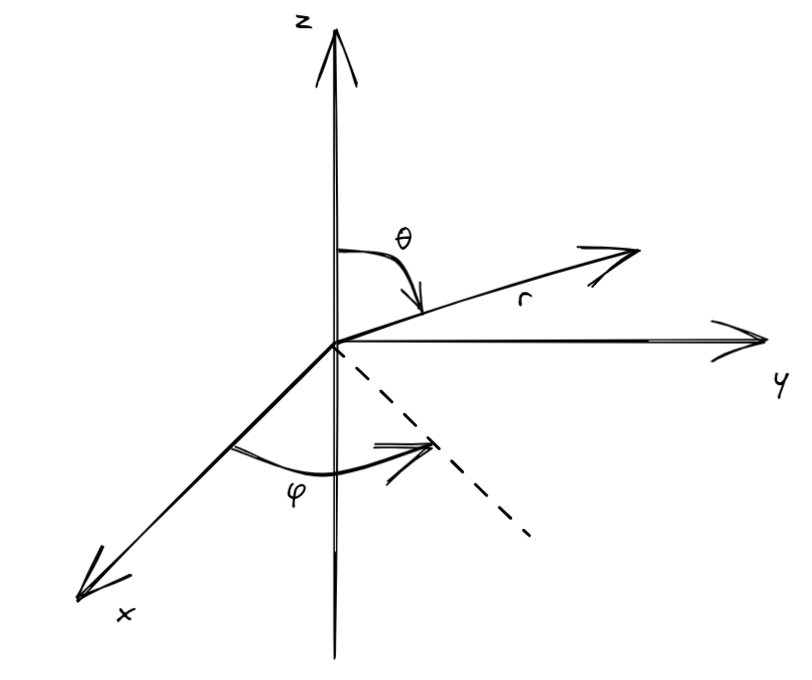
附圆柱坐标系下旋度表达式:
∇ × A ⃗ = 1 ρ ∣ e ⃗ p ρ e ϕ → e z → ∂ ∂ ρ ∂ ∂ ϕ ∂ ∂ z A p ρ A ϕ A z ∣ \nabla \times \vec{A}=\frac{1}{\rho}\left|\begin{array}{ccc} \vec{e}_{p} & \rho \overrightarrow{e_{\phi}} & \overrightarrow{e_{z}} \\ \frac{\partial}{\partial \rho} & \frac{\partial}{\partial \phi} & \frac{\partial}{\partial z} \\ A_{p} & \rho A_{\phi} & A_{z} \end{array}\right| ∇×A=ρ1 ep∂ρ∂Apρeϕ∂ϕ∂ρAϕez∂z∂Az
三、分离变量法
(1)分别描述利用标量电位计算电偶极子电场和利用矢量磁位计算磁偶极子磁场各自的优点。
(2)简述镜像法的理论基础:唯一性定理,以及镜像法的基本步骤。
(3)在电场强度为 E 0 → \overrightarrow{E_0} E0 的真空中放置一半径为 a a a 的无限长理想导体圆柱,柱的轴线与电场相互垂直,导体接地,求空间电位分布以及柱面上的自由电荷密度。
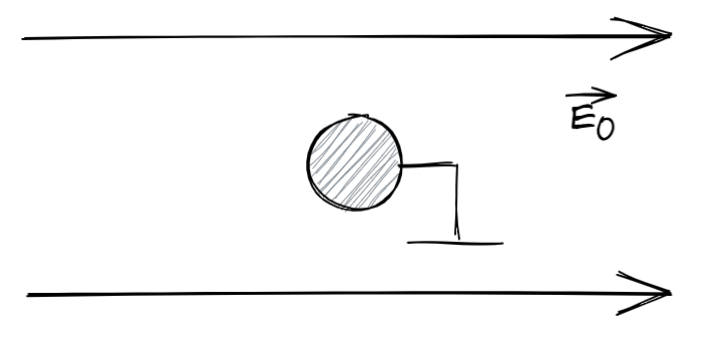
拉普拉斯方程在柱坐标系下的通解:
ϕ ( ρ , φ ) = A 0 + B 0 ln ρ + ∑ n = 1 ∞ ( A n ρ n + B n ρ − n ) [ C n cos ( n φ ) + D n sin ( n φ ) ] \phi(\rho, \varphi)=A_{0}+B_{0} \ln \rho+\sum_{n=1}^{\infty}\left(A_{n} \rho^{n}+B_{n} \rho^{-n}\right)\left[C_{n} \cos (n \varphi)+D_{n} \sin (n \varphi)\right] ϕ(ρ,φ)=A0+B0lnρ+n=1∑∞(Anρn+Bnρ−n)[Cncos(nφ)+Dnsin(nφ)]
此题的解答可以参考论文 袁海良.外电场中接地圆柱形导体内、外的电场、电势及面电荷分布[J].青海师范大学民族师范学院学报,2011,22(01):90-91.DOI:10.13780
四、均匀平面波的反射与透射
(1)给出均匀平面波斜入射时的入射平面定义,并说明什么是垂直极化入射波,什么是平行极化入射波。
(2)太阳光以布儒斯特角照射到玻璃上,是否存在反射光?为什么?
(3)一均匀平面波,入射波电场为 E i → = e ⃗ x 120 cos ( 3 π × 1 0 8 t − 10 π z ) V / m \overrightarrow{E_{i}}=\vec{e}_{x} 120 \cos \left(3 \pi \times 10^{8}t-10 \pi z\right) \mathrm{V} / \mathrm{m} Ei=ex120cos(3π×108t−10πz)V/m ,自空气(媒质1)垂直入射到一个无损耗、不导电的媒质(媒质2)上,分界面处 z = 0 z = 0 z=0。媒质2的相对介电系数 ε r \varepsilon_{r} εr = 4,相对磁导率 μ r \mu_{r} μr = 1,请计算媒质1中的反射波电场振幅的大小以及驻波比(或驻波系数),定义为合成波的电场强度的最大值和最小值之比,并给出媒质1中反射波的电场表达式。
附菲涅尔公式:
R L = E R 0 E 10 = η 2 cos θ 1 − η 1 cos θ 2 η 2 cos θ 1 + η 1 cos θ 2 R 11 = E R 0 E 10 = η 1 H R 0 η 1 H 10 = η 1 cos θ 1 − η 2 cos θ 2 η 1 cos θ 1 + η 2 cos θ 2 T 1 = E T 0 E 10 = 2 η 2 cos θ 1 η 2 cos θ 1 + η 1 cos θ 2 T 11 = E T 0 E 10 = η 2 H T 0 η 1 H 10 = 2 η 2 cos θ 1 η 1 cos θ 1 + η 2 cos θ 2 \begin{array}{ll} R_{L}=\frac{E_{R 0}}{E_{10}}=\frac{\eta_{2} \cos \theta_{1}-\eta_{1} \cos \theta_{2}}{\eta_{2} \cos \theta_{1}+\eta_{1} \cos \theta_{2}} & R_{11}=\frac{E_{R_{0}}}{E_{10}}=\frac{\eta_{1} H_{R 0}}{\eta_{1} H_{10}}=\frac{\eta_{1} \cos \theta_{1}-\eta_{2} \cos \theta_{2}}{\eta_{1} \cos \theta_{1}+\eta_{2} \cos \theta_{2}} \\ T_{1}=\frac{E_{T 0}}{E_{10}}=\frac{2 \eta_{2} \cos \theta_{1}}{\eta_{2} \cos \theta_{1}+\eta_{1} \cos \theta_{2}} & T_{11}=\frac{E_{T 0}}{E_{{ }^{10}}}=\frac{\eta_{2} H_{T_{0}}}{\eta_{1} H_{10}}=\frac{2 \eta_{2} \cos \theta_{1}}{\eta_{1} \cos \theta_{1}+\eta_{2} \cos \theta_{2}} \end{array} RL=E10ER0=η2cosθ1+η1cosθ2η2cosθ1−η1cosθ2T1=E10ET0=η2cosθ1+η1cosθ22η2cosθ1R11=E10ER0=η1H10η1HR0=η1cosθ1+η2cosθ2η1cosθ1−η2cosθ2T11=E10ET0=η1H10η2HT0=η1cosθ1+η2cosθ22η2cosθ1
五、时变电磁场与均匀平面波在无界空间中的传播
已知自由空间的均匀平面波的电场表达式为 E ⃗ = 600 π ( − e x → s + e z → δ ) e − j π ( δ x − 6 z ) V / m \vec{E}=600 \pi\left(-\overrightarrow{e_{x}} s+\overrightarrow{e_{z}} \delta\right) e^{-j \pi(\delta x-6 z)} \mathrm{V} / \mathrm{m} E=600π(−exs+ezδ)e−jπ(δx−6z)V/m ,式中s为常数。
求:该平面波的
(1)波矢量;
(2)波长和频率;
(3)s的值;
(4)相伴磁场的瞬时表达式;
(5)平均坡印廷矢量;
(6)极化状态;
(7)该电磁波如果在
ε
r
=
81
\varepsilon_{r}=81
εr=81,
μ
r
=
1
\mu_{r}=1
μr=1,
σ
=
4
δ
/
m
\sigma=4 \delta / \mathrm{m}
σ=4δ/m 的海水中传播,最少传多远就可以认为其已消失殆尽(即其电场强度幅值减小到原来的1/1000以下)?
导电介质中的电磁波:
传播常数为 β = ω 2 μ ε 2 1 + ( σ ω ε ) 2 + 1 \beta=\sqrt{\frac{\omega^{2} \mu \varepsilon}{2}} \sqrt{\sqrt{1+\left(\frac{\sigma}{\omega \varepsilon}\right)^{2}}+1} β=2ω2με1+(ωεσ)2+1
衰减常数为 α = ω 2 μ ε 2 1 + ( σ ω ε ) 2 − 1 \alpha=\sqrt{\frac{\omega^{2} \mu \varepsilon}{2}} \sqrt{\sqrt{1+\left(\frac{\sigma}{\omega \varepsilon}\right)^{2}}-1} α=2ω2με1+(ωεσ)2−1
六、导行电磁波
(1)简述纵向分量法的处理规则波导问题的思路;
(2)矩形波导横截面为 a x b = 12.5 x 7.5 m m 2 mm^2 mm2 ,按顺序写出截至波长最长的前三个传输模;
(3)若上述波导中填充 ε r = 2 \varepsilon_{r}=2 εr=2, μ r = 1 \mu_{r}=1 μr=1 的理想介质,频率为16GHz的电磁波进入波导后将以哪几种模式工作?
七、电磁辐射
(1)简述滞后位法中“滞后”的含义;
(2)沿z轴放置的电基本振子在空间场分布如下式:
E
r
=
k
3
I
Δ
l
cos
θ
2
π
ω
ε
[
1
(
k
r
)
2
−
j
(
k
r
)
3
]
e
−
j
k
r
E
θ
=
k
3
I
Δ
sin
θ
2
π
ω
ε
[
j
k
r
+
1
(
k
r
)
2
−
j
(
k
r
)
3
]
e
−
i
k
r
H
ϕ
=
k
2
I
Δ
sin
θ
4
π
[
j
k
r
+
1
(
k
r
)
2
]
e
−
j
k
r
E
ϕ
=
H
r
=
H
θ
=
0
\begin{array}{l} E_{r}=\frac{k^{3} I \Delta l \cos \theta}{2 \pi \omega \varepsilon}\left[\frac{1}{(k r)^{2}}-\frac{j}{(k r)^{3}}\right] e^{-j k r} \\ E_{\theta}=\frac{k^{3} I \Delta \sin \theta}{2 \pi \omega \varepsilon}\left[\frac{j}{k r}+\frac{1}{(k r)^{2}}-\frac{j}{(k r)^{3}}\right] e^{-i k r} \\ H_{\phi}=\frac{k^{2} I \Delta \sin \theta}{4 \pi}\left[\frac{j}{k r}+\frac{1}{(k r)^{2}}\right] e^{-j k r} \\ E_{\phi}=H_{r}=H_{\theta}=0 \end{array}
Er=2πωεk3IΔlcosθ[(kr)21−(kr)3j]e−jkrEθ=2πωεk3IΔsinθ[krj+(kr)21−(kr)3j]e−ikrHϕ=4πk2IΔsinθ[krj+(kr)21]e−jkrEϕ=Hr=Hθ=0
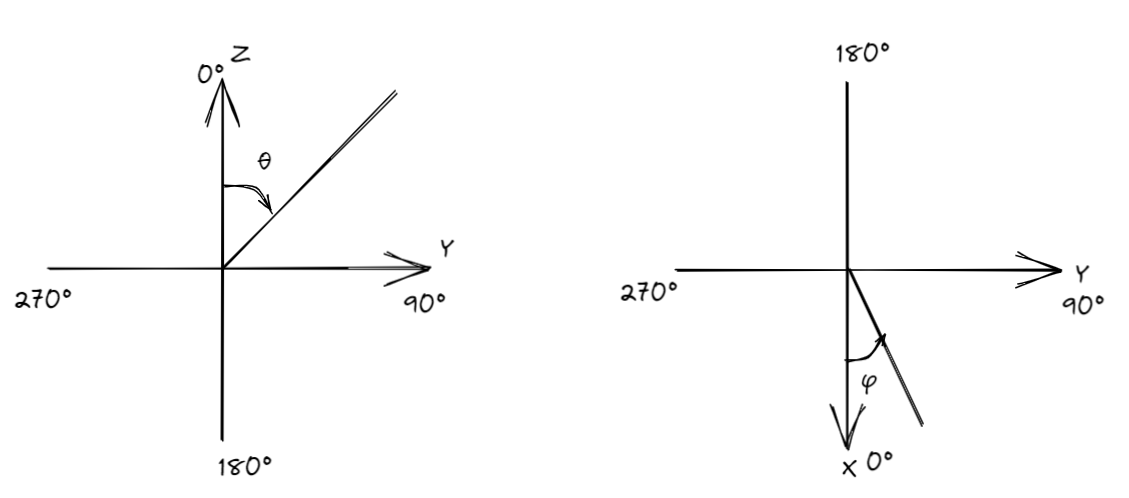
写出近区场( k r ≪ 1 kr \ll 1 kr≪1)和远区辐射场( k r ≫ 1 kr \gg 1 kr≫1)的表达式,写出远区辐射场的方向性函数,并在下面的图中画出远区辐射场在yz平面和xy平面的方向性图。
往年真题回忆
2022春电磁场期末回忆版(待考证)
简答:
边界条件,唯一性定理意义,滞后位,波导三个传播方式。
计算:
球的电场分布,镜像法算个做功,分离变量法,两个课后题原题,波导传播模式,远区电磁场。
2022秋电磁场期末回忆版
1.解释安培环路定理的适用条件 简单界面 x<0 真空 x>0 介质 E 0 E_0 E0,分界面上 x = 0 电荷密度 ρ s \rho_s ρs,已知 X<0 电场分布, 求x>0电场分布,求点场内极化电荷密度。
2.分离变量法直角坐标系;简述镜像法原理。
3.已知H,求如上例题参数,以及伴随电场,最后解释肌肤深度及其公式。
4.解释分界面 垂直极化波 平行极化波概念;已知反射波和入射波的功率比值,和介质2的u,求其相对介电常数。
5.解释纵向分量法处理规则波导的思路 以及矩形波导的传输波长判断哪些模可以传播。
6.写远场电磁场的场分布公式,解释其电场和磁场的相位关系。
复习建议
期末试题与上述样题大同小异,复习时以书为主,解释简述类题目在书上有对应描述,复习时理解概念,考前反复记忆。计算类型题目多数为课本例题以及部分课后习题,复习时以例题和作业为主,过于复杂的题目可以跳过。
相关资源以及部分答案已经归档至公众号【AIShareLab】,回复 电磁场与电磁波 可以获取。