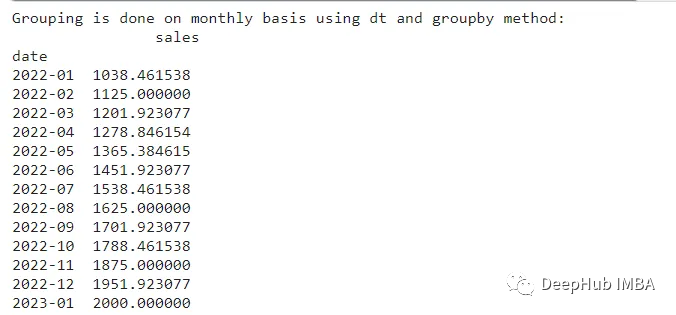
一、题目
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
二、示例
2.1> 示例 1:

提示:
0< grid.length <=2000< grid[0].length <=200
三、解题思路
根据题目描述,我们需要计算出一条获取礼物的路径,确保按照这条路径走下来之后,可以拿到最多的礼物价值。那么在题目中,我们先来挖掘出一下关键的信息:
【礼物价值】每个礼物的价值都
大于0;
【起点】左上角格子;
【终点】右下角格子;
【行走步数】每次只能走1个格子;
【行走方向】只能向右或者向下移动;(最关键的信息!!)
那么,了解了题目中给出的关键点,我们就可以尝试移动一下,以下图为例,我们从【格子1】开始移动,可以向右移动,那么礼物总价值是1+3=4;也可以向下移动,那么礼物总价值是1+1=2;
所以,我们定义dp[i][j],用于表示在grid[i][j]格子出,最大的礼物总价值;我们以下图中格子3为例,能够到达这个格子只能是从格子1走过来(因为格子3的上面已经没有格子了),那么格子3的dp就等于4。而我们再来看格子5,到达它的路径就有两条:一条是从格子3向下走过来;另一条就是从第二行的格子1向右走过来的。那么由于dp是表示最大的礼物总价值,所以我们通过对比,可以知道从格子3向下走到格子5之后,总礼物价值是9;而从第二行的格子1向右走到格子5之后,礼物总价值是7;由于9大于7,所以格子5的dp等于9;依次类推,遍历整个二维数组grid,那么右下角的dp值就是这道题的答案了。
为了更好的演示计算过程,请见下图的计算过程:

【说明】
- 左上角五角星表示起始点;
- 右下角五角星表示结束点;
- 箭头表示可能行走的路径;
- 圆圈表示到达某个格子后,总的礼物价值;
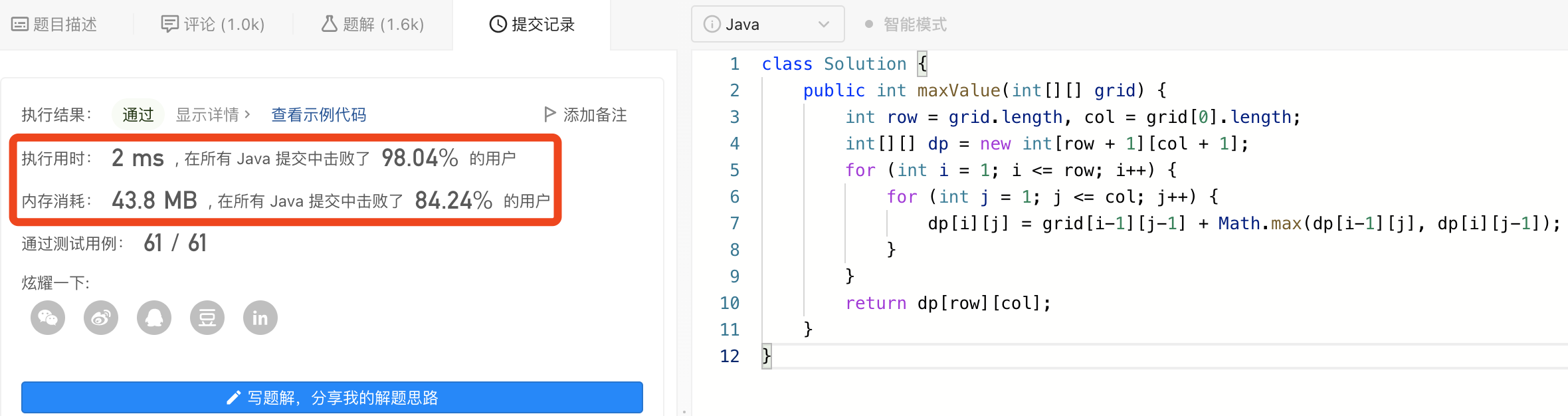
四、代码实现
class Solution {
public int maxValue(int[][] grid) {
int row = grid.length, col = grid[0].length;
int[][] dp = new int[row + 1][col + 1];
for (int i = 1; i <= row; i++) {
for (int j = 1; j <= col; j++) {
dp[i][j] = grid[i-1][j-1] + Math.max(dp[i-1][j], dp[i][j-1]);
}
}
return dp[row][col];
}
}
今天的文章内容就这些了:
写作不易,笔者几个小时甚至数天完成的一篇文章,只愿换来您几秒钟的 点赞 & 分享 。
更多技术干货,欢迎大家关注公众号“爪哇缪斯” ~ \(^o^)/ ~ 「干货分享,每天更新」