回溯
- 1.回溯问题
- 77.组合
- 216.组合总和|||
- 17.电话号码的字母组合
- 39.组合总和
- 40.组合总和||
- 131.分割回文串
- 93.复原IP地址
- 78.子集
- 90.子集||
- 491.递增子序列
- 46.全排列
- 47.全排列||
- 51.N皇后
- 37.解数独
1.回溯问题
77.组合

思路:
回溯的本质是用一棵树来描述,用path来存路径,当path满足条件时直接返回即可。然后把最后一个节点pop出去,这样递归的来实现。
List<Integer> path=new ArrayList<Integer>();//路径上的元素
List<List<Integer>> result=new ArrayList<List<Integer>>();//收集的结果集
public List<List<Integer>> combine(int n, int k) {
combinehelper(n,k,1);
return result;
}
public void combinehelper(int n,int k,int startIndex) {//startIndex代表从哪开始遍历
if(path.size()==k) {
result.add(new ArrayList<>(path));
return ;
}
//右边的参数是剪枝操作,当i在这个下标后边时,后边就不需要去遍历了,因为后边的元素都加上也不够k个元素了
for(int i=startIndex;i<=n-(k-path.size())+1;i++) {
path.add(i);
//递归操作
combinehelper(n,k,i+1);
//回溯操作,如果12,满足条件后,会把2弹出来,让3进去
path.remove(path.size()-1);
}
}
216.组合总和|||

思路:
当path的数量满足题目要求时,并且路径和等于题目数量时,就可以保存
List<Integer> path=new ArrayList<>();
List<List<Integer>> result=new ArrayList<List<Integer>>();
public List<List<Integer>> combinationSum3(int k, int n) {
combin(k,n,1,0);
return result;
}
public void combin(int k,int n,int startIndex,int sum) {
if(path.size()==k) {
if(sum==n) {
result.add(new ArrayList<>(path));
return ;
}
}
//剪枝操作,如果sum大于targetsum,直接剪枝
if(sum>n) {
return ;
}
for(int i=startIndex;i<=9-(k-path.size())+1;i++) {
path.add(i);
sum+=i;
combin(k,n,i+1,sum);
//回溯操作
path.remove(path.size()-1);
sum-=i;
}
}
17.电话号码的字母组合
思路:
用index来表示当前遍历到第几个字母了。
遍历到的字母,用一个for循环,把每次遍历到的字母加进去。然后进行递归操作,然后进行回溯操作。
当index==输入数字的长度时,就进行终止操作
List<String > list=new ArrayList<String>();//用来存储结果
//初始对应所有的数字,为了直接对应2-9,新增了两个无效的字符串""
String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
public List<String> letterCombinations(String digits) {
if(digits==null||digits.length()==0) {
return list;
}
//调用递归程序
letter(digits,0);
return list;
}
StringBuilder letter=new StringBuilder();//letter表示每个节点的元素
public void letter(String digits,int index) {//index标识当前遍历到几个字母了
if(index==digits.length()) {//当index==digits的长度时,就终止。
list.add(letter.toString());
return ;
}
//将字母转成数字
int temp=digits.charAt(index)-'0';
//将数字转换成对应的字母
String str=numString[temp];
for(int i=0;i<str.length();i++) {
letter.append(str.charAt(i));
letter(digits,index+1);
letter.deleteCharAt(letter.length()-1);
}
}
39.组合总和

思路:
确定好终止条件,当sum==tartget的时候,返回结果即可。
递归的参数要包括当前的起始位置。
List<Integer> path=new ArrayList<Integer>();//每组符合条件的值
List<List<Integer>> result=new ArrayList<List<Integer>>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
combin(candidates,target,0,0);
return result;
}
public void combin(int []candidates,int target,int sum,int startIndex) {
//确定终止条件
if(sum==target) {
result.add(new ArrayList<>(path));
}
for(int i=startIndex;i<candidates.length;i++) {
//进行剪枝操作
if(sum>target) {
return ;
}
path.add(candidates[i]);
sum+=candidates[i];
combin(candidates,target,sum,i);//初始位置要从当前条件开始;因为题目中的要求同一个元素允许使用多次
//进行回溯操作
path.remove(path.size()-1);
sum-=candidates[i];
}
}
40.组合总和||

思路:
这道题主要是怎么去重,用一个used数组,如果该数字用过,标记为true,如果没有用过,标记为false,然后把数组排一个序,如果当前元素和前一个元素一样,并且used标识的前一个数组没有用过,那么这个场景。就可以忽略了。为啥要用used呢,因为有可能出现112这种情况,当1用过之后,往下遍历的时候。第二个1也需要使用,那么这种情况就不可以忽略,所以需要用used数组来标识。
List<Integer> path=new ArrayList<Integer>();//每组符合条件的值
List<List<Integer>> result=new ArrayList<List<Integer>>();
boolean used[];//用来去重的操作
public List<List<Integer>> combinationSum(int[] candidates, int target) {
used=new boolean[candidates.length];
Arrays.sort(candidates);//将数组排好序,方便去重操作
combin(candidates,target,0,0,used);
return result;
}
public void combin(int []candidates,int target,int sum,int startIndex,boolean[]used) {
//确定终止条件
if(sum==target) {
result.add(new ArrayList<>(path));
}
for(int i=startIndex;i<candidates.length;i++) {
//进行剪枝操作
if(sum>target) {
return ;
}
//去重操作
if(i>0&&candidates[i]==candidates[i-1]&&!used[i-1]) {//当used[i-1]为false的时候,表示前一个没有被用过,这样可以进行树枝去重,如果不拿
//这个判断的话,那么112这种情况也会被排除掉
continue;
}
path.add(candidates[i]);
sum+=candidates[i];
used[i]=true;
combin(candidates,target,sum,i+1,used);//初始位置要从当前条件开始;因为题目中的要求同一个元素允许使用多次
//进行回溯操作
path.remove(path.size()-1);
sum-=candidates[i];
used[i]=false;
}
}
131.分割回文串
思路:
这道题的思路是用stratindex来标识分隔符,然后判断startindex到i的子串是不是回文串,如果是,则加入,如果不是则开始下一次循环。例如aab,startindex=0,然后i+1之后,去更新起始位置,变成startindex=1,然后i每次加一,这样一次循环之后,就会将a,a,b加入结果数组中。然后再看倒数第二次,当b被弹出之后,startindex=1,i=3,此时ab不满足提议,continue之后跳出循环,然后将a也弹出。这样进入第一层循环,找startindex=1的子串去了。
List<String> path=new ArrayList<String>();
List<List<String>> result=new ArrayList<List<String>> ();
public List<List<String>> partition(String s) {
partitionhelp(s,0);
return result;
}
public void partitionhelp(String s,int startIndex) {
//判断终止条件,如果startIndex>=s.length,那么就终止来收集结果
if(startIndex>=s.length()) {
result.add(new ArrayList<>(path));
return ;
}
//单层递归逻辑
for(int i=startIndex;i<s.length();i++) {
//判断从startIndex开始到i是不是回文字符串,如果是,则收集结果
if(isPalindrome(s,startIndex,i)) {
path.add(s.substring(startIndex,i+1));
}else {
//如果不是,直接开始下一层循环。
continue;
}
partitionhelp(s,i+1);
//进行回溯操作,把最后一次加入的结果弹出去
path.remove(path.size()-1);
}
}
//判断是否是回文串
private boolean isPalindrome(String s, int startIndex, int end) {
for (int i = startIndex, j = end; i < j; i++, j--) {
if (s.charAt(i) != s.charAt(j)) {
return false;
}
}
return true;
}
93.复原IP地址

思路:
用逗点来标志是不是逗了3个,如果是,判断最后一段字符串是不是合法,如果合法,就可以收入到结果集当中了。判断是不是合法的思路呢,字符串里不应该有字母,0开头的数字不合法,如果大于255了也不合法。
然后startindex代表的是分隔符,如果判断好了,就在str的后边加一个逗点。
List<String> result = new ArrayList<>();
public List<String> restoreIpAddresses(String s) {
if (s.length() > 12) return result; // 算是剪枝了
backTrack(s, 0, 0);
return result;
}
// startIndex: 搜索的起始位置, pointNum:添加逗点的数量
private void backTrack(String s, int startIndex, int pointNum) {
if (pointNum == 3) {// 逗点数量为3时,分隔结束
// 判断第四段⼦字符串是否合法,如果合法就放进result中
if (isValid(s,startIndex,s.length()-1)) {
result.add(s);
}
return;
}
for (int i = startIndex; i < s.length(); i++) {
if (isValid(s, startIndex, i)) {
s = s.substring(0, i + 1) + "." + s.substring(i + 1); //在str的后⾯插⼊⼀个逗点
pointNum++;
backTrack(s, i + 2, pointNum);// 插⼊逗点之后下⼀个⼦串的起始位置为i+2
pointNum--;// 回溯
s = s.substring(0, i + 1) + s.substring(i + 2);// 回溯删掉逗点
} else {
break;
}
}
}
// 判断字符串s在左闭⼜闭区间[start, end]所组成的数字是否合法
private Boolean isValid(String s, int start, int end) {
if (start > end) {
return false;
}
if (s.charAt(start) == '0' && start != end) { // 0开头的数字不合法
return false;
}
int num = 0;
for (int i = start; i <= end; i++) {
if (s.charAt(i) > '9' || s.charAt(i) < '0') { // 遇到⾮数字字符不合法
return false;
}
num = num * 10 + (s.charAt(i) - '0');
if (num > 255) { // 如果⼤于255了不合法
return false;
}
}
return true;
}
78.子集
思路:
这道题的区别就是不一定要在叶子节点去收集结果,而是在每个节点都去收集结果,即进入第二次循环时就要去收集结果。
List<Integer> path=new ArrayList<Integer>();
List<List<Integer>> result=new ArrayList<List<Integer>>();
public List<List<Integer>> subsets(int[] nums) {
subset(nums,0);
return result;
}
public void subset(int []nums,int startIndex) {
//不需要判断终止条件,每次都要收集结果
result.add(new ArrayList<Integer>(path));
if(startIndex>=nums.length) {
return ;
}
for(int i=startIndex;i<nums.length;i++) {
path.add(nums[i]);
//收集一个节点之后进入下一层叶子
subset(nums,i+1);
//进行回溯操作
path.remove(path.size()-1);
}
}
90.子集||
思路:
用used数组来进行去重,先把数组排好序,当后边的元素和前边的元素一样时并且前边的元素还没有用过的时候,这样可以直接跳过。
List<Integer> path=new ArrayList<Integer>();
List<List<Integer>> result=new ArrayList<List<Integer>>();
boolean []used;
public List<List<Integer>> subsetsWithDup(int[] nums) {
Arrays.sort(nums);
used=new boolean[nums.length];
subset(nums,0,used);
return result;
}
public void subset(int []nums,int startIndex,boolean[]used) {
//不需要判断终止条件,每次都要收集结果
result.add(new ArrayList<Integer>(path));
if(startIndex>=nums.length) {
return ;
}
for(int i=startIndex;i<nums.length;i++) {
//进行去重操作
if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false) {
continue;
}
path.add(nums[i]);
used[i]=true;
//收集一个节点之后进入下一层叶子
subset(nums,i+1,used);
//进行回溯操作
path.remove(path.size()-1);
used[i]=false;
}
}
491.递增子序列
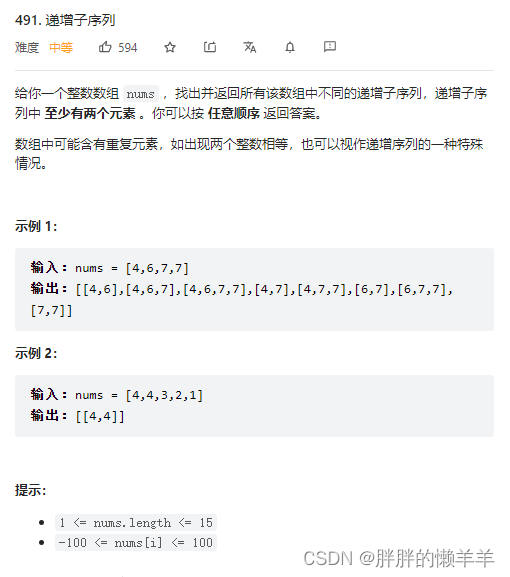
思路:
这道题不能先排序再去重,因为对于6467来说,排完序之后是4667.而原序列根本没这个序列,所以就不符合题意。
而在每层递归的时候,要保证后面的元素要比最后一个元素大才行,并且这个元素前边没有用过。如果用过的话,前面算出的结果肯定会包含后边的数字的。
List<Integer> path=new ArrayList<Integer>();
List<List<Integer>> result=new ArrayList<List<Integer>> ();
public List<List<Integer>> findSubsequences(int[] nums) {
findSub(nums,0);
return result;
}
public void findSub(int[]nums,int startIndex) {
if(path.size()>1) {
result.add(new ArrayList<>(path));//当数组长度大于等于2时,就可以收集结果了
}
boolean []used=new boolean[201];//定义一个去重数组
for(int i=startIndex;i<nums.length;i++) {
if(!path.isEmpty()&&nums[i]<path.get(path.size()-1)||used[nums[i]+100]) {//这里是或者,因为只要这两个条件任意满足一个都不符合题意
continue;
}
used[nums[i]+100]=true;//将这个数字标志为用过
path.add(nums[i]);
findSub(nums,i+1);
//回溯操作
path.remove(path.size()-1);//used数组不用remove,因为这里每层循环都会重新生成一个数组
}
}
46.全排列

思路:
这里每次遍历都从0开始,用used数组标记这个元素有没有使用过,如果使用过,那么直接跳过即可。
List<Integer> path=new ArrayList<>();
List<List<Integer>> result=new ArrayList<List<Integer>>();
public List<List<Integer>> permute(int[] nums) {
boolean[]used=new boolean[nums.length];
premu(nums,used);
return result;
}
public void premu(int []nums,boolean[]used) {
if(path.size()==nums.length) {
//条件满足,可以收菜了
result.add(new ArrayList<>(path));
}
for(int i=0;i<nums.length;i++) {
if(used[i]==true) {//当用过了这个数,直接跳过
continue;
}
used[i]=true;
path.add(nums[i]);
premu(nums,used);
//进行回溯
used[i]=false;
path.remove(path.size()-1);
}
}
47.全排列||

思路:
因为数组中有重复的数字,先把数组排好序,然后加上去重的逻辑。
List<Integer> path=new ArrayList<>();
List<List<Integer>> result=new ArrayList<List<Integer>>();
public List<List<Integer>> permuteUnique(int[] nums) {
//先把数组排个序
Arrays.sort(nums);
boolean[]used=new boolean[nums.length];
premu(nums,used);
return result;
}
public void premu(int []nums,boolean[]used) {
if(path.size()==nums.length) {
//条件满足,可以收菜了
result.add(new ArrayList<>(path));
}
for(int i=0;i<nums.length;i++) {
//加上去重的逻辑,因为有重复的数字
if(i>0&&nums[i]==nums[i-1]&&used[i-1]==true) {
continue;
}
if(used[i]==true) {//当用过了这个数,直接跳过
continue;
}
used[i]=true;
path.add(nums[i]);
premu(nums,used);
//进行回溯
used[i]=false;
path.remove(path.size()-1);
}
}
51.N皇后
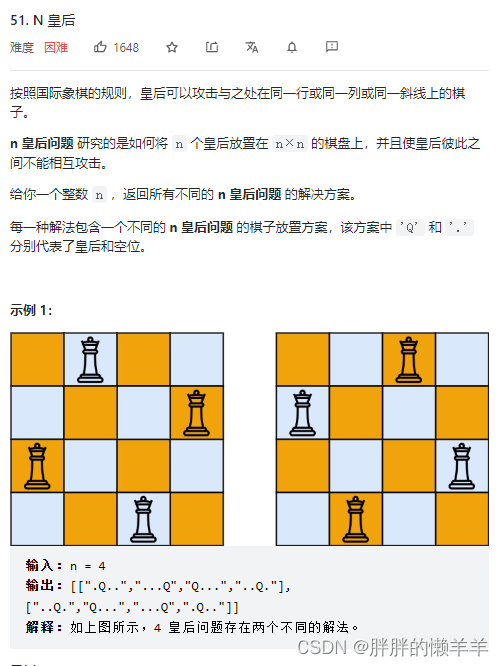
思路:
用回溯的知识,每层数上代表一行,然后这一层数依次放一个,当第二层开始时,先要判断皇后的位置满不满足条件,如果满足条件再放,如果不满足,就不要放了。
怎么判断皇后的位置是否满足条件呢,先判断当前列上的位置有没有皇后,然后往左上角45度方向找,然后往右上角135度方向找,如果都没有皇后,那么就是满足题意的。
List<List<String>> res = new ArrayList<>();
public boolean isValid(int row, int col, int n, char[][] chessboard) {
// 检查列
for (int i=0; i<row; ++i) { // 相当于剪枝
if (chessboard[i][col] == 'Q') {
return false;
}
}
// 检查45度对角线
for (int i=row-1, j=col-1; i>=0 && j>=0; i--, j--) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
// 检查135度对角线
for (int i=row-1, j=col+1; i>=0 && j<=n-1; i--, j++) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
return true;
}
public List Array2List(char[][] chessboard) {
List<String> list = new ArrayList<>();
for (char[] c : chessboard) {
list.add(String.copyValueOf(c));
}
return list;
}
public List<List<String>> solveNQueens(int n) {
char[][] chessboard = new char[n][n];
for (char[] c : chessboard) {
Arrays.fill(c, '.');
}
backTrack(n, 0, chessboard);
return res;
}
/**
*
* @param n 棋盘的行数
* @param row 遍历到第几行了
* @param chessboard 棋盘
*/
public void backTrack(int n,int row,char [][]chessboard) {
if(row==n) {
res.add(Array2List(chessboard));
return ;
}
//每行从0开始
for(int col=0;col<n;col++) {
if(isValid(row,col,n,chessboard)) {
chessboard[row][col] = 'Q';
backTrack(n, row+1, chessboard);
chessboard[row][col] = '.';
}
}
}
37.解数独
思路:
要两层循环,每次判断有空格的位置,依次放入1-9,判断它是不是合法,如果合法,直接返回true即可。
怎么判断是不是合法呢,现在行中看有没有重复的数字,再看列中有没有重复的数字。然后查看当前的9宫格里有没有重复的数字。