电子技术——系统性分析反馈电压放大器

在本节我们提供一个系统性的分析反馈电压放大器的方法。首先我们考虑反馈网络没有负载效应理想情况,其次我们考虑反馈网络有限阻抗下的非理想情况。总之,这种方法的思路在于,将非理想情况转换为理想情况中的A电路和 β \beta β 电路。
理想情况
正如我们之前提到的,反馈网络在理想情况下本质是一个理想压控压源,如图:
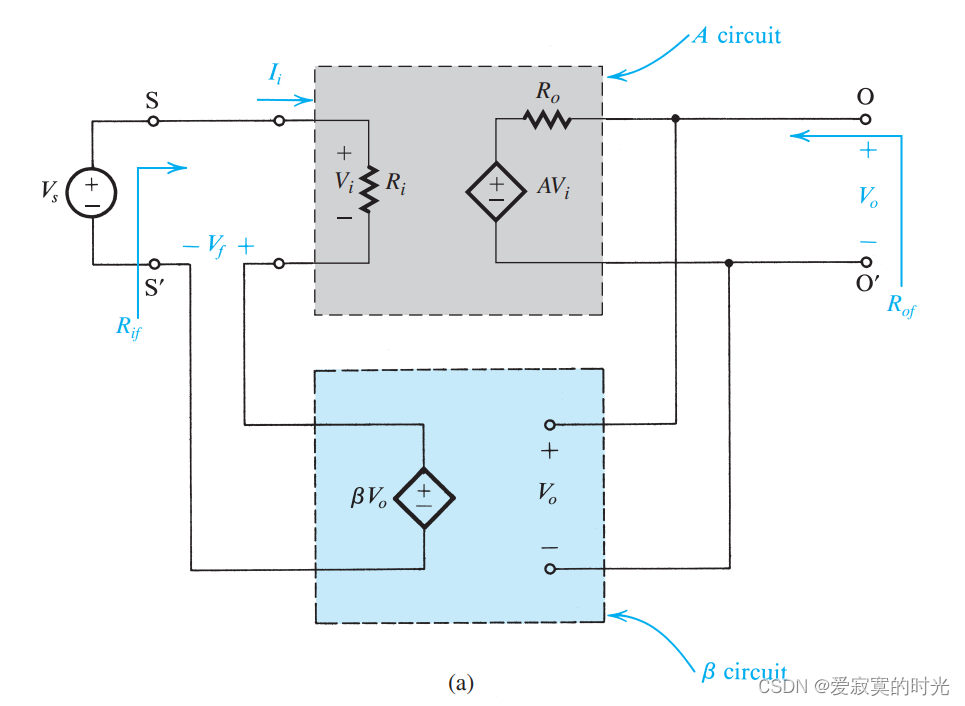
它由一个单边的开环放大器(A 电路)和一个理想的电压采样、混合器反馈网络(
β
\beta
β 电路)组成。其中A 电路具有差分输入阻抗
R
i
R_i
Ri 和开路增益
A
A
A 以及输出阻抗
R
o
R_o
Ro 。我们假设信号源是理想的阻抗为零,并且输出开路。我们注意,
β
\beta
β 电路没有负载效应,也就是说,将
β
\beta
β 电路分离之后,A 电路的开路增益
A
A
A 不变。
这个电路完全符合第一节的理想反馈模型,因此:
A f = A 1 + A β A_f = \frac{A}{1 + A\beta} Af=1+AβA
等效的模型如下:
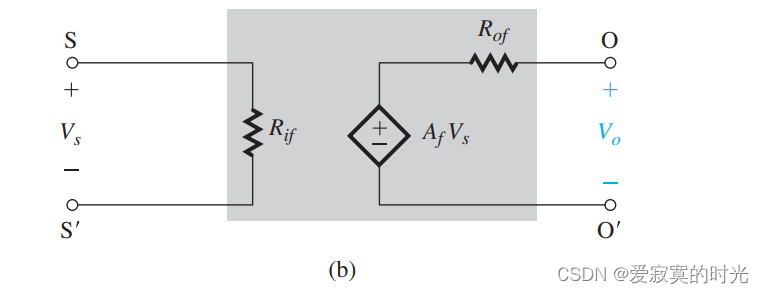
其中
R
i
f
R_{if}
Rif 和
R
o
f
R_{of}
Rof 是等效输入输出阻抗。根据第一节的公式,我们知道:
V i = V s 1 + A β V_i = \frac{V_s}{1 + A\beta} Vi=1+AβVs
则输入电流为:
I i = V i R i = V s ( 1 + A β ) R i I_i = \frac{V_i}{R_i} = \frac{V_s}{(1 + A\beta) R_i} Ii=RiVi=(1+Aβ)RiVs
则根据戴维南等效:
R i f ≡ V s I i = ( 1 + A β ) R i R_{if} \equiv \frac{V_s}{I_i} = (1 + A\beta) R_i Rif≡IiVs=(1+Aβ)Ri
因此,和期望中的一致,负反馈网络提高了放大器的输入阻抗到反馈量倍。
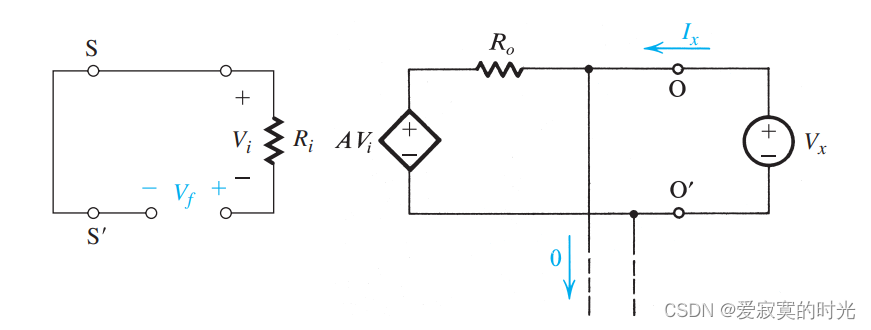
接下来决定等效输出阻抗。我们将信号源置零,并在输出端放置测试电压源:
I
x
=
V
x
−
A
V
i
R
o
I_x = \frac{V_x - AV_i}{R_o}
Ix=RoVx−AVi
其中:
V i = − V f = − β V x V_i = -V_f = -\beta V_x Vi=−Vf=−βVx
得到:
R o f = R o 1 + A β R_{of} = \frac{R_o}{1 + A\beta} Rof=1+AβRo
同样的,反馈网络降低了放大器的输出阻抗,降低了反馈量倍。
实际情况
现在在实际情况下,反馈网络不再是理想压控压源,而是具有输入输入输出阻抗的压控压源。即等效于给定下面的电路图:
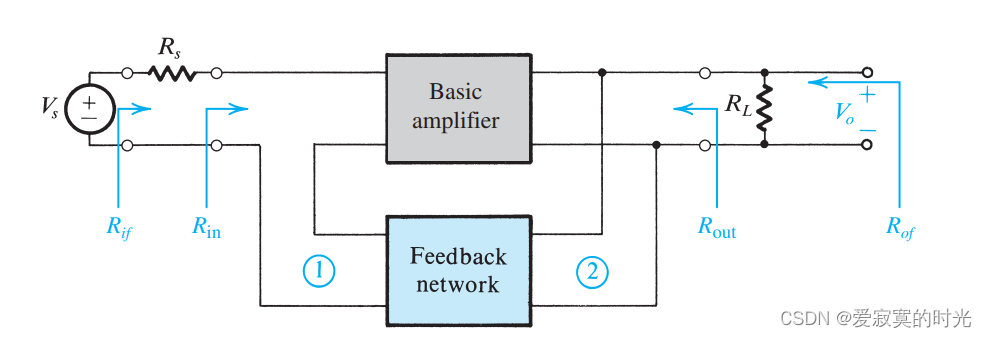
求其等效的A 电路和
β
\beta
β 电路。我们的思路是将信号源内阻
R
s
R_s
Rs 和反馈网络输出阻抗(负载效应)
R
11
R_{11}
R11 放入A 电路中。将负载电阻
R
L
R_L
RL 和反馈网络输出阻抗(负载效应)
R
22
R_{22}
R22 放入A 电路中,这样就做到了将问题转换为理想情况,如下图:
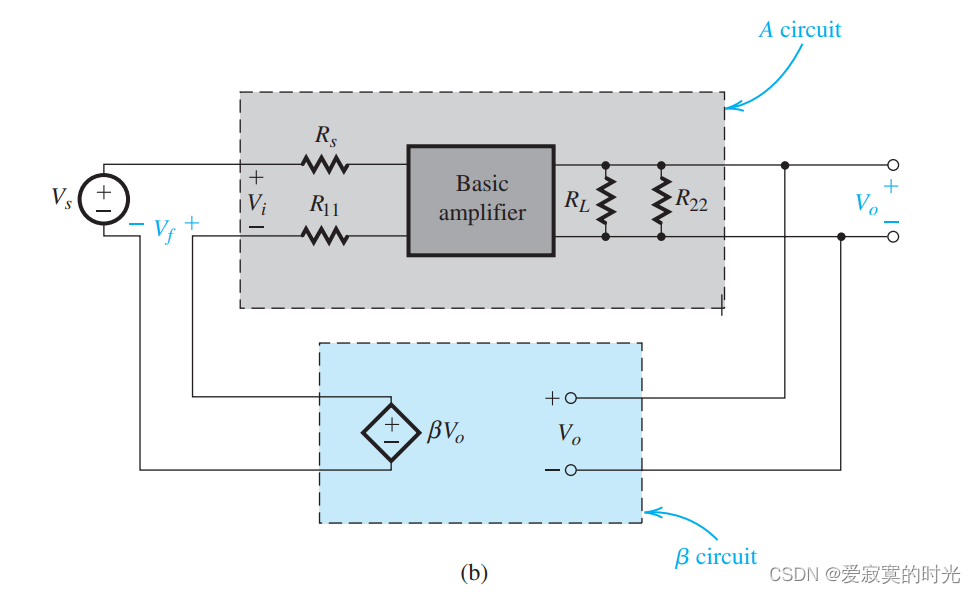
其中 R 11 R_{11} R11 是从下图中1端口看过去的阻抗(注意2端口短路), R 22 R_{22} R22 是从2端口看过去的阻抗(注意1端口开路),这和压控压源的阻抗定义一致。
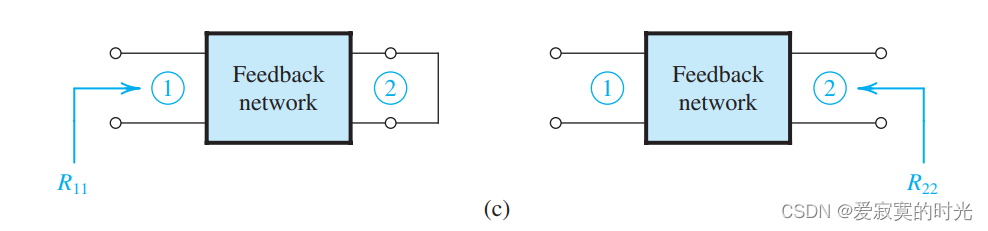
我们使用下面的电路估计
β
\beta
β :
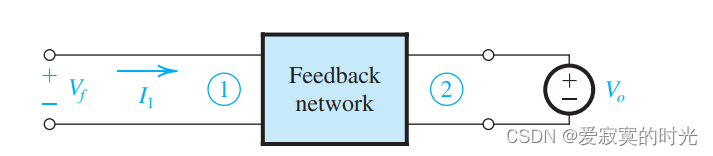
在原反馈网络中:
β ≡ V f V o ∣ I 1 = 0 \beta \equiv \frac{V_f}{V_o} |_{I_1 = 0} β≡VoVf∣I1=0
等效电压增益为:
A = V i V o A = \frac{V_i}{V_o} A=VoVi
估计闭环增益为:
A f ≡ V o V s = A 1 + A β A_f \equiv \frac{V_o}{V_s} = \frac{A}{1 + A\beta} Af≡VsVo=1+AβA
另外:
R i f = R i ( 1 + A β ) R_{if} = R_i(1 + A\beta) Rif=Ri(1+Aβ)
R o f = R o / ( 1 + A β ) R_{of} = R_o/(1 + A\beta) Rof=Ro/(1+Aβ)
观察到 $R_{in} 和 R s R_s Rs 串联,则有:
R i n = R i f − R s R_{in} = R_{if} - R_s Rin=Rif−Rs
同样的, R L R_L RL 和 R o u t R_{out} Rout 并联,则有:
R o u t = 1 / ( 1 R o f − 1 R L ) R_{out} = 1 / (\frac{1}{R_{of}} - \frac{1}{R_L}) Rout=1/(Rof1−RL1)
需要注意的是,上述方法仍然只是一种估计方法,因为我们忽略了反馈网络的传导特性。并且,我们假设放大器是单边的,不存在内部的反馈,所有的反馈都发生在外部的反馈网络中。




![CSS字体样式(font)[详细]](https://img-blog.csdnimg.cn/13aef95f583a487bb1e7596a85db308b.png)