刚体上的两个点速度之间的关系

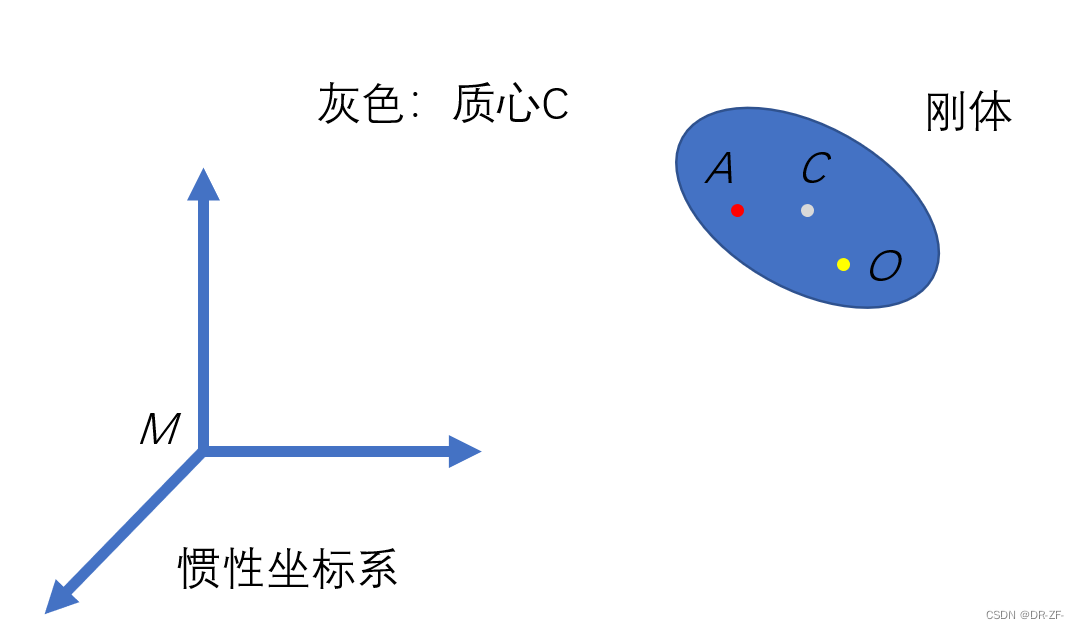
注意：这里所讨论的都是投影在惯性坐标系上的。

$$d_{{}_{MA}}=d_{{}_{MO}}+d_{{}_{OA}}=d_{{}_{MO}}+d_{{}_{CA}}-d_{{}_{CO}}$$

求导

$${\dot{d}}_{{}_{MA}}={\dot{d}}_{{}_{MO}}+{\dot{d}}_{{}_{CA}}-{\dot{d}}_{{}_{CO}}$$

即

$$v_{{}_A}=v_{{}_O}+{\mathbf{\omega }}^{\times }{d}_{{}_{CA}}-{\mathbf{\omega }}^{\times }{d}_{{}_{CO}}=v_{{}_O}+{\mathbf{\omega }}^{\times }{d}_{{}_{OA}}$$

如果把这个投影到刚体本体系中依然成立。