目录
支持向量机SVM的详细原理
SVM的定义
SVM理论
Libsvm工具箱详解
简介
参数说明
易错及常见问题
SVM应用实例,基于SVM的股票价格预测
支持向量机SVM的详细原理
SVM的定义
支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;SVM还包括核技巧,这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化,可形式化为一个求解凸二次规划的问题,也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。
(1)支持向量机(Support Vector Machine, SVM)是一种对数据进行二分类的广义线性分类器,其分类边界是对学习样本求解的最大间隔超平面。
(2)SVM使用铰链损失函数计算经验风险并在求解系统中加入了正则化项以优化结构风险,是一个具有稀疏性和稳健性的分类器 。
(3)SVM可以通过引入核函数进行非线性分类。
SVM理论
1,线性可分性

2,损失函数


3,核函数


Libsvm工具箱详解
简介
LIBSVM是台湾大学林智仁(Lin Chih-Jen)教授等开发设计的一个简单、易于使用和快速有效的SVM模式识别与回归的软件包,他不但提供了编译好的可在Windows系列系统的执行文件,还提供了源代码,方便改进、修改以及在其它操作系统上应用;该软件对SVM所涉及的参数调节相对比较少,提供了很多的默认参数,利用这些默认参数可以解决很多问题;并提供了交互检验(Cross Validation)的功能。该软件可以解决C-SVM、ν-SVM、ε-SVR和ν-SVR等问题,包括基于一对一算法的多类模式识别问题。
主要参数说明
Options:可用的选项即表示的涵义如下
-s svm类型:SVM设置类型(默认0)
0 – C-SVC
1 --v-SVC
2 – 一类SVM
3 – e -SVR
4 – v-SVR
-t 核函数类型:核函数设置类型(默认2)
0 – 线性:u’v
1 – 多项式:(ru’v + coef0)^degree
2 – RBF函数:exp(-r|u-v|^2)
3 –sigmoid:tanh(ru’v + coef0)
-d degree:核函数中的degree设置(针对多项式核函数)(默认3)
-g r(gama):核函数中的gamma函数设置(针对多项式/rbf/sigmoid核函数)(默认1/ k)
-r coef0:核函数中的coef0设置(针对多项式/sigmoid核函数)((默认0)
-c cost:设置C-SVC,e -SVR和v-SVR的参数(损失函数)(默认1)
-n nu:设置v-SVC,一类SVM和v- SVR的参数(默认0.5)
-p p:设置e -SVR 中损失函数p的值(默认0.1)
-m cachesize:设置cache内存大小,以MB为单位(默认40)
-e eps:设置允许的终止判据(默认0.001)
-h shrinking:是否使用启发式,0或1(默认1)
-wi weight:设置第几类的参数C为weight*C(C-SVC中的C)(默认1)
-v n: n-fold交互检验模式,n为fold的个数,必须大于等于2
其中-g选项中的k是指输入数据中的属性数。option -v 随机地将数据剖分为n部分并计算交互检验准确度和均方根误差。以上这些参数设置可以按照SVM的类型和核函数所支持的参数进行任意组合,如果设置的参数在函数或SVM类型中没有也不会产生影响,程序不会接受该参数;如果应有的参数设置不正确,参数将采用默认值。
具体对应解释如下:
svm类别
指定SVM的类型,下面是可能的取值:
CvSVM::C_SVC C类支持向量分类机。 n类分组 (n \geq 2),允许用异常值惩罚因子C进行不完全分类。
CvSVM::NU_SVC \nu类支持向量分类机。n类似然不完全分类的分类器。参数为 \nu 取代C(其值在区间【0,1】中,nu越大,决策边界越平滑)。
CvSVM::ONE_CLASS 单分类器,所有的训练数据提取自同一个类里,然后SVM建立了一个分界线以分割该类在特征空间中所占区域和其它类在特征空间中所占区域。
CvSVM::EPS_SVR \epsilon类支持向量回归机。训练集中的特征向量和拟合出来的超平面的距离需要小于p。异常值惩罚因子C被采用。
CvSVM::NU_SVR \nu类支持向量回归机。 \nu 代替了 p。
kernel_type –
SVM的内核类型,下面是可能的取值:
CvSVM::LINEAR 线性内核。没有任何向映射至高维空间,线性区分(或回归)在原始特征空间中被完成,这是最快的选择。K(x_i, x_j) = x_i^T x_j.
CvSVM::POLY 多项式内核: K(x_i, x_j) = (\gamma x_i^T x_j + coef0)^{degree}, \gamma > 0.
CvSVM::RBF 基于径向的函数,对于大多数情况都是一个较好的选择: K(x_i, x_j) = e^{-\gamma ||x_i - x_j||^2}, \gamma > 0.
CvSVM::SIGMOID Sigmoid函数内核:K(x_i, x_j) = \tanh(\gamma x_i^T x_j + coef0).
degree – 内核函数(POLY)的参数degree。
gamma – 内核函数(POLY/ RBF/ SIGMOID)的参数\gamma。
coef0 – 内核函数(POLY/ SIGMOID)的参数coef0。
Cvalue – SVM类型(C_SVC/ EPS_SVR/ NU_SVR)的参数C。
nu – SVM类型(NU_SVC/ ONE_CLASS/ NU_SVR)的参数 \nu。
p – SVM类型(EPS_SVR)的参数 \epsilon。
class_weights – C_SVC中的可选权重,赋给指定的类,乘以C以后变成 class_weights_i * C。所以这些权重影响不同类别的错误分类惩罚项。权重越大,某一类别的误分类数据的惩罚项就越大。
term_crit – SVM的迭代训练过程的中止条件,解决部分受约束二次最优问题。您可以指定的公差和/或最大迭代次数。
易错及调参注意事项
1,分类和回归容易搞错,分类-s参数为1,回归-s参数为1
2,bestc参数分类的时候调小,回归的时候调大。
3,安装libsvm参数的时候,工具箱自带的参数容易和matlab自带的冲突,要做好协调
SVM应用实例
基于SVM的股票价格预测MATLAB代码
tic;
close all;
clear;
clc;
format compact;
%% 数据的提取和预处理
% 载入测试数据上证指数(1990.12.19-2009.08.19)
% 数据是一个4579*6的double型的矩阵,每一行表示每一天的上证指数
% 6列分别表示当天上证指数的开盘指数,指数最高值,指数最低值,收盘指数,当日交易量,当日交易额.
load chapter14_sh.mat;
% 提取数据
[m,n] = size(sh);
ts = sh(2:m,1);
tsx = sh(1:m-1,:);
% 画出原始上证指数的每日开盘数
figure;
plot(ts,‘LineWidth’,2);
title(‘上证指数的每日开盘数(1990.12.20-2009.08.19)’,‘FontSize’,12);
xlabel(‘交易日天数(1990.12.19-2009.08.19)’,‘FontSize’,12);
ylabel(‘开盘数’,‘FontSize’,12);
grid on;
% 数据预处理,将原始数据进行归一化
ts = ts’;
tsx = tsx’;
% mapminmax为matlab自带的映射函数
% 对ts进行归一化
[TS,TSps] = mapminmax(ts,1,2);
% 画出原始上证指数的每日开盘数归一化后的图像
figure;
plot(TS,‘LineWidth’,2);
title(‘原始上证指数的每日开盘数归一化后的图像’,‘FontSize’,12);
xlabel(‘交易日天数(1990.12.19-2009.08.19)’,‘FontSize’,12);
ylabel(‘归一化后的开盘数’,‘FontSize’,12);
grid on;
% 对TS进行转置,以符合libsvm工具箱的数据格式要求
TS = TS’;
% mapminmax为matlab自带的映射函数
% 对tsx进行归一化
[TSX,TSXps] = mapminmax(tsx);
% 对TSX进行转置,以符合libsvm工具箱的数据格式要求
TSX = TSX’;
%% 选择回归预测分析最佳的SVM参数c&g
% 首先进行粗略选择:
[bestmse,bestc,bestg] = SVMcgForRegress(TS,TSX,-8,8,-8,8);
% 打印粗略选择结果
disp(‘打印粗略选择结果’);
str = sprintf( ‘Best Cross Validation MSE = %g Best c = %g Best g = %g’,bestmse,bestc,bestg);
disp(str);
% 根据粗略选择的结果图再进行精细选择:
[bestmse,bestc,bestg] = SVMcgForRegress(TS,TSX,-4,4,-4,4,3,0.5,0.5,0.05);
% 打印精细选择结果
disp(‘打印精细选择结果’);
str = sprintf( ‘Best Cross Validation MSE = %g Best c = %g Best g = %g’,bestmse,bestc,bestg);
disp(str);
%% 利用回归预测分析最佳的参数进行SVM网络训练
cmd = ['-c ', num2str(bestc), ’ -g ‘, num2str(bestg) , ’ -s 3 -p 0.01’];
model = svmtrain(TS,TSX,cmd);
%% SVM网络回归预测
[predict,mse] = svmpredict(TS,TSX,model);
predict = mapminmax(‘reverse’,predict’,TSps);
predict = predict’;
% 打印回归结果
str = sprintf( ‘均方误差 MSE = %g 相关系数 R = %g%%’,mse(2),mse(3)*100);
disp(str);
%% 结果分析
figure;
hold on;
plot(ts,‘-o’);
plot(predict,‘r-^’);
legend(‘原始数据’,‘回归预测数据’);
hold off;
title(‘原始数据和回归预测数据对比’,‘FontSize’,12);
xlabel(‘交易日天数(1990.12.19-2009.08.19)’,‘FontSize’,12);
ylabel(‘开盘数’,‘FontSize’,12);
grid on;
figure;
error = predict - ts’;
plot(error,‘rd’);
title(‘误差图(predicted data - original data)’,‘FontSize’,12);
xlabel(‘交易日天数(1990.12.19-2009.08.19)’,‘FontSize’,12);
ylabel(‘误差量’,‘FontSize’,12);
grid on;
figure;
error = (predict - ts’)./ts’;
plot(error,‘rd’);
title(‘相对误差图(predicted data - original data)/original data’,‘FontSize’,12);
xlabel(‘交易日天数(1990.12.19-2009.08.19)’,‘FontSize’,12);
ylabel(‘相对误差量’,‘FontSize’,12);
grid on;
snapnow;
toc;
%% 子函数 SVMcgForRegress.m
% function [mse,bestc,bestg] = SVMcgForRegress(train_label,train,cmin,cmax,gmin,gmax,v,cstep,gstep,msestep)
% %SVMcg cross validation by faruto
%
% %
% % by faruto
% %Email:patrick.lee@foxmail.com QQ:516667408 http://blog.sina.com.cn/faruto BNU
% %last modified 2010.01.17
% %Super Moderator @ www.ilovematlab.cn
%
% % 若转载请注明:
% % faruto and liyang , LIBSVM-farutoUltimateVersion
% % a toolbox with implements for support vector machines based on libsvm, 2009.
% % Software available at http://www.ilovematlab.cn
% %
% % Chih-Chung Chang and Chih-Jen Lin, LIBSVM : a library for
% % support vector machines, 2001. Software available at
% % http://www.csie.ntu.edu.tw/~cjlin/libsvm
%
% % about the parameters of SVMcg
% if nargin < 10
% msestep = 0.06;
% end
% if nargin < 8
% cstep = 0.8;
% gstep = 0.8;
% end
% if nargin < 7
% v = 5;
% end
% if nargin < 5
% gmax = 8;
% gmin = -8;
% end
% if nargin < 3
% cmax = 8;
% cmin = -8;
% end
% % X:c Y:g cg:acc
% [X,Y] = meshgrid(cmin:cstep:cmax,gmin:gstep:gmax);
% [m,n] = size(X);
% cg = zeros(m,n);
%
% eps = 10^(-4);
%
% bestc = 0;
% bestg = 0;
% mse = Inf;
% basenum = 2;
% for i = 1:m
% for j = 1:n
% cmd = [‘-v ‘,num2str(v),’ -c ‘,num2str( basenum^X(i,j) ),’ -g ‘,num2str( basenum^Y(i,j) ),’ -s 3 -p 0.1’];
% cg(i,j) = svmtrain(train_label, train, cmd);
%
% if cg(i,j) < mse
% mse = cg(i,j);
% bestc = basenum^X(i,j);
% bestg = basenum^Y(i,j);
% end
%
% if abs( cg(i,j)-mse )<=eps && bestc > basenum^X(i,j)
% mse = cg(i,j);
% bestc = basenum^X(i,j);
% bestg = basenum^Y(i,j);
% end
%
% end
% end
% % to draw the acc with different c & g
% [cg,ps] = mapminmax(cg,0,1);
% figure;
% [C,h] = contour(X,Y,cg,0:msestep:0.5);
% clabel(C,h,‘FontSize’,10,‘Color’,‘r’);
% xlabel(‘log2c’,‘FontSize’,12);
% ylabel(‘log2g’,‘FontSize’,12);
% firstline = ‘SVR参数选择结果图(等高线图)[GridSearchMethod]’;
% secondline = [‘Best c=’,num2str(bestc),’ g=‘,num2str(bestg), …
% ’ CVmse=’,num2str(mse)];
% title({firstline;secondline},‘Fontsize’,12);
% grid on;
%
% figure;
% meshc(X,Y,cg);
% % mesh(X,Y,cg);
% % surf(X,Y,cg);
% axis([cmin,cmax,gmin,gmax,0,1]);
% xlabel(‘log2c’,‘FontSize’,12);
% ylabel(‘log2g’,‘FontSize’,12);
% zlabel(‘MSE’,‘FontSize’,12);
% firstline = ‘SVR参数选择结果图(3D视图)[GridSearchMethod]’;
% secondline = [‘Best c=’,num2str(bestc),’ g=‘,num2str(bestg), …
% ’ CVmse=’,num2str(mse)];
% title({firstline;secondline},‘Fontsize’,12);
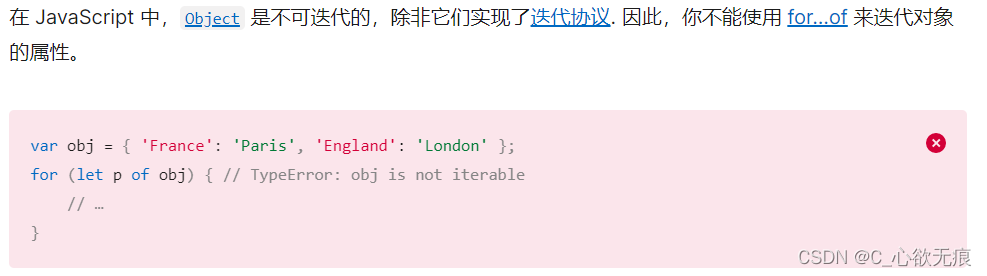
效果图







结果分析
从效果图看,SVM能很好的实现股票价格的预测,相对于传统的二分类SVM,libsvm工具箱,不仅能实现多分类,还可以实现回归分析,大大扩展了SVM的应用范围,在很多方面,特别小样本难训练的问题的应用方面,SVM拥有特别的优势







![数学(二)-- LeetCode[204] 计数质数](https://img-blog.csdnimg.cn/8ce0247b32994186897b4afde1aa098c.gif#pic_center)