paper:Like What You Like: Knowledge Distill via Neuron Selectivity Transfer
code:https://github.com/megvii-research/mdistiller/blob/master/mdistiller/distillers/NST.py
本文的创新点
本文探索了一种新型的知识 - 神经元的选择性知识,并将其传递给学生模型。这个模型背后的直觉相当简单:每个神经元本质上从原始输入提取与特定任务相关的某种模式,因此,如果一个神经元在某些区域或样本中被激活,这意味着这些区域或样本共享一些与该任务相关的特性。这种聚类知识对学生模型非常有价值,因为它为教室模型的最终预测结果提供了一种解释。因此,作者提出对齐教师模型和学生模型神经元选择模式的分布。
背景
Notions
假定教师模型和学生模型都是卷积神经网络,并将教师模型表示为 \(T\),学生模型表示为 \(S\)。CNN中某一层的输出特征图表示为 \(\mathbf{F}\in \mathbb{R}^{C\times HW}\),\(\mathbf{F}\) 的每一行即每个通道的特征图表示为 \(\mathbf{f}^{k\cdot}\in \mathbb{R}^{HW}\),\(\mathbf{F}\) 的每一列即每个空间位置沿所有通道的激活表示为 \(\mathbf{f}^{\cdot k}\in \mathbb{R}^{C}\)。\(\mathbf{F}_{T}\) 和 \(\mathbf{F}_{S}\) 分别表示教师模型和学生模型中某一层的特征图,不失一般性,我们假设 \(\mathbf{F}_{T}\) 和 \(\mathbf{F}_{S}\) 的大小相等,如果不相等则可以通过插值使它们相等。
Maximum Mean Discrepancy
最大平均差异(Maximum Mean Discrepancy,MMD)可以看作是一种概率分布间的距离度量,基于从它们采样的样本。假设我们有两组分别从分布 \(p\) 和 \(q\) 中采样的样本 \(\mathcal{X}=\left \{ x^{i} \right \}^{N}_{i=1} \) 和 \(\mathcal{Y}=\left \{ y^{j} \right \}^{M}_{j=1} \),那么 \(p\) 和 \(q\) 之间的MMD距离的平方如下
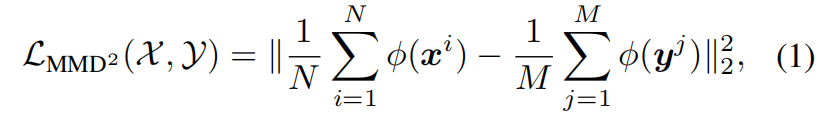
其中 \(\phi \left ( \cdot \right ) \) 是一个显示映射函数,通过进一步扩展并应用核技巧(kernel trick),式(1)可以表示为

其中 \(k(\cdot,\cdot)\) 是一个核函数,它将样本向量投射到一个更高维或是无限维的特征空间中。
最小化MMD等价于最小化 \(p\) 和 \(q\) 之间的距离。
方法介绍
Motivation
下面是两张叠加了热力图(heat map)的图片,其中热力图是根据VGG16 Conv5_3中的某个神经元得到的。从图中很容易看出这两个神经元具有很强的选择性:左图的神经元对猴子的脸部非常敏感,右侧的神经元对字符非常敏感。这种激活实际上意味着神经元的选择性,即什么样的输入可以触发这些神经元。换句话说,一个神经元高激活的区域可能共享一些与任务相关的相似特性,尽管这些特性可能对于人类没有非常直观的解释。

为了捕获这些相似特性,在学生模型中也应该有神经元模仿这些激活模式。因此本文提出了一种新的知识类型:神经元选择性(neuron selectivities)或者叫做共激活(co-activations),并将其传递给学生模型。
Formulation
每个通道的特征图 \(\mathbf{f}^{k\cdot}\) 示一个特定神经元的selectivity知识,我们定义Neuron Selectivity Transfer,NST损失如下
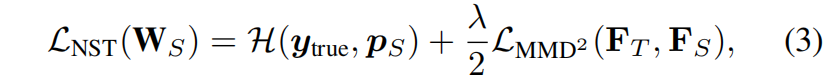
其中 \(\mathcal{H}\) 是交叉熵损失,\(\mathbb{y}_{true}\) 是ground truth标签,\(p_{S}\) 是学生模型的输出概率。
MMD损失可以扩展如下

其中用 \(l_{2}\) 标准化后的 \(\frac{\mathbf{f}^{k\cdot} }{\left \|\mathbf{f}^{k\cdot} \right \|_{2} } \) 替代了 \(\mathbf{f}^{k\cdot}\),这是为了使每个样本具有相同的尺度。最小化MMD损失就等价于将神经元的选择性知识传递给学生模型。
Choice of Kernels
本文选用以下三种核函数
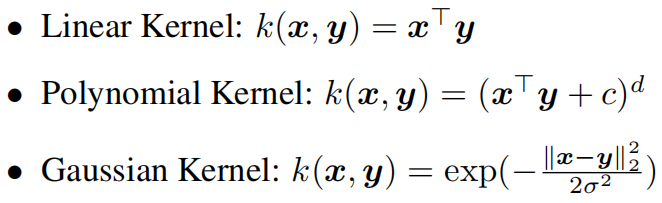
对于多项式核,本文设置 \(d=2,c=0\)。对于高斯核,\(\sigma ^{2}\) 设置为对应距离的平方。
代码解析
import torch
import torch.nn as nn
import torch.nn.functional as F
from ._base import Distiller
def nst_loss(g_s, g_t):
return sum([single_stage_nst_loss(f_s, f_t) for f_s, f_t in zip(g_s, g_t)])
def single_stage_nst_loss(f_s, f_t):
s_H, t_H = f_s.shape[2], f_t.shape[2]
if s_H > t_H:
f_s = F.adaptive_avg_pool2d(f_s, (t_H, t_H))
elif s_H < t_H:
f_t = F.adaptive_avg_pool2d(f_t, (s_H, s_H))
f_s = f_s.view(f_s.shape[0], f_s.shape[1], -1) # (64,64,32,32)->(64,64,1024)
f_s = F.normalize(f_s, dim=2)
f_t = f_t.view(f_t.shape[0], f_t.shape[1], -1)
f_t = F.normalize(f_t, dim=2)
return (
poly_kernel(f_t, f_t).mean().detach()
+ poly_kernel(f_s, f_s).mean()
- 2 * poly_kernel(f_s, f_t).mean()
)
def poly_kernel(a, b):
a = a.unsqueeze(1) # (64,64,1024)->(64,1,64,1024)
b = b.unsqueeze(2) # (64,64,1024)->(64,64,1,1024)
res = (a * b).sum(-1).pow(2) # (64,64,64,1024)->(64,64,64)
return res
class NST(Distiller):
"""
Like What You Like: Knowledge Distill via Neuron Selectivity Transfer
"""
def __init__(self, student, teacher, cfg):
super(NST, self).__init__(student, teacher)
self.ce_loss_weight = cfg.NST.LOSS.CE_WEIGHT
self.feat_loss_weight = cfg.NST.LOSS.FEAT_WEIGHT
def forward_train(self, image, target, **kwargs):
logits_student, feature_student = self.student(image) # (64,3,32,32)
with torch.no_grad():
_, feature_teacher = self.teacher(image)
# losses
loss_ce = self.ce_loss_weight * F.cross_entropy(logits_student, target)
loss_feat = self.feat_loss_weight * nst_loss(
feature_student["feats"][1:], feature_teacher["feats"][1:]
# [torch.Size([64, 64, 32, 32]), torch.Size([64, 128, 16, 16]), torch.Size([64, 256, 8, 8])]
# [torch.Size([64, 64, 32, 32]), torch.Size([64, 128, 16, 16]), torch.Size([64, 256, 8, 8])]
)
losses_dict = {
"loss_ce": loss_ce,
"loss_kd": loss_feat,
}
return logits_student, losses_dict