贝叶斯分类法（Bayes）

贝叶斯分类算法是统计学的一种分类方法，它是一类利用概率统计知识进行分类的算法。

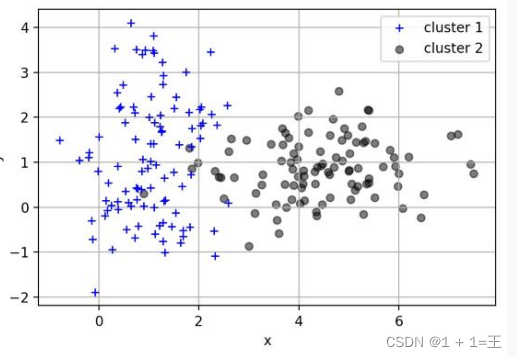
• 优点：所需估计的参数少，对于缺失数据不敏感；有着坚实的数学基础，以及稳定的分类效率。
• 缺点：需要假设属性之间相互独⽴，这往往并不成⽴；需要知道先验概率；分类决策存在错误率。

决策树（Decision Tree）

决策树（Decision Tree）是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。

决策树是一种树形结构，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别。

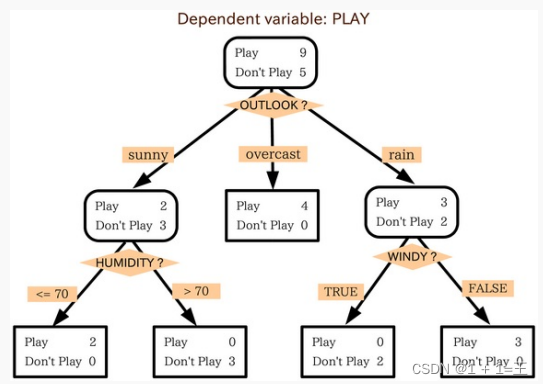
• 优点：不需要任何领域知识或参数假设；适合⾼维数据；短时间内处理⼤量数据，得到可⾏且效果较好的结果；能够同时处理数据型和常规性属性。
• 缺点：对于各类别样本数量不⼀致数据，信息增益偏向于那些具有更多数值的特征；易于过拟合；忽略属性之间的相关性；不⽀持在线学习。

支持向量机（SVM）

支持向量机是一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面。

• 优点：可以解决⼩样本下机器学习的问题；提⾼泛化性能；可以解决⾼维、⾮线性问题。
• 缺点：对缺失数据敏感；内存消耗⼤，难以解释；运行和调参麻烦。

K近邻（K-NN）

KNN方法的思路是：在特征空间中，如果一个样本附近的k个最近(即特征空间中最邻近)样本的大多数属于某一个类别，则该样本也属于这个类别。

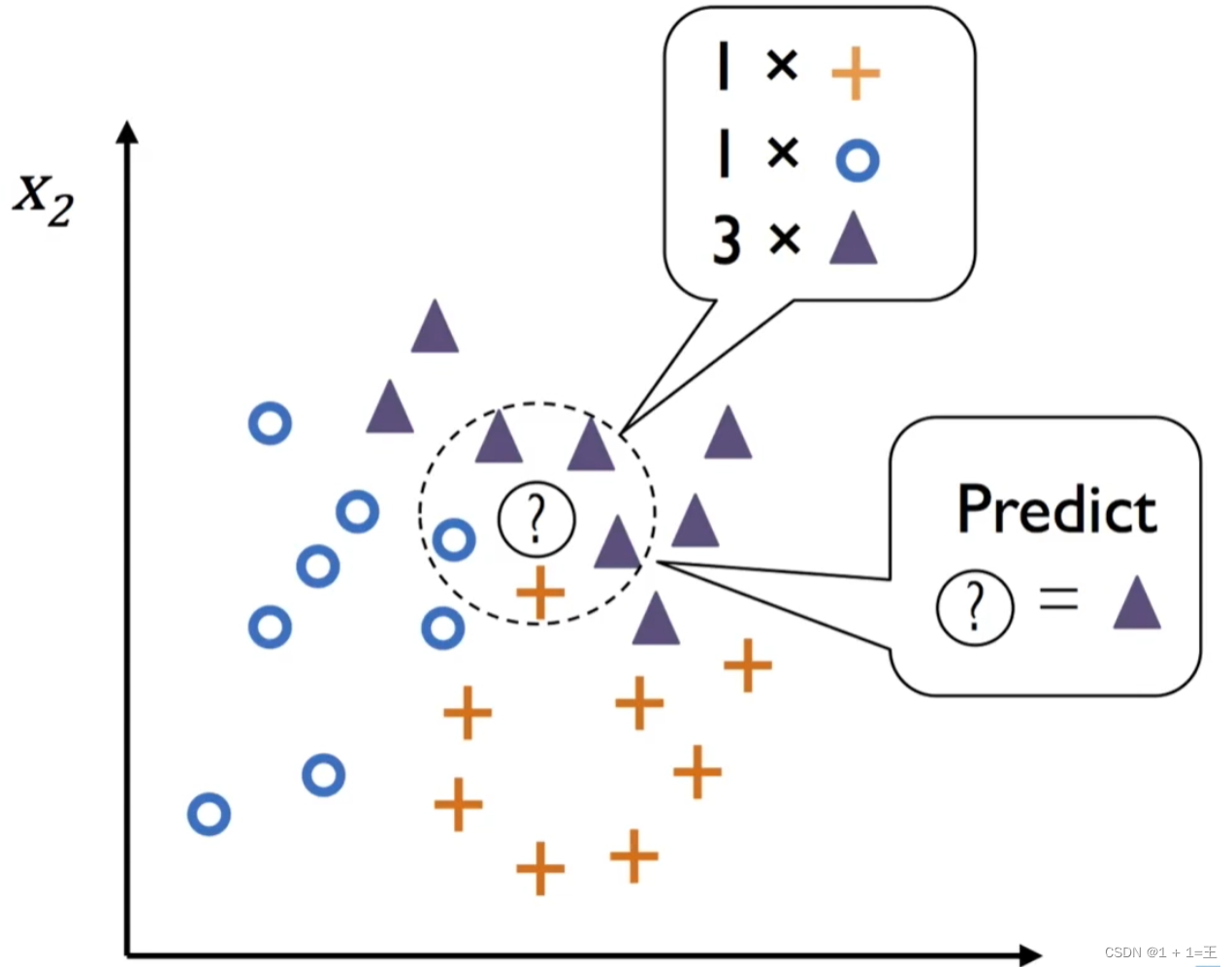
• 优点：可⽤于⾮线性分类；训练时间复杂度为O(n)；准确度⾼，对数据没有假设，对outlier不敏感；既可以⽤来做分类也可以⽤来做回归。
• 缺点：计算量太⼤；对于样本分类不均衡的问题，会产⽣误判；需要⼤量的内存；输出的可解释性不强。

逻辑回归（Logistics Regression）

逻辑回归也称作logistic回归分析，是一种广义的线性回归分析模型，属于机器学习中的监督学习。其推导过程与计算方式类似于回归的过程，但实际上主要是用来解决二分类问题（也可以解决多分类问题）。通过给定的n组数据（训练集）来训练模型，并在训练结束后对给定的一组或多组数据（测试集）进行分类。

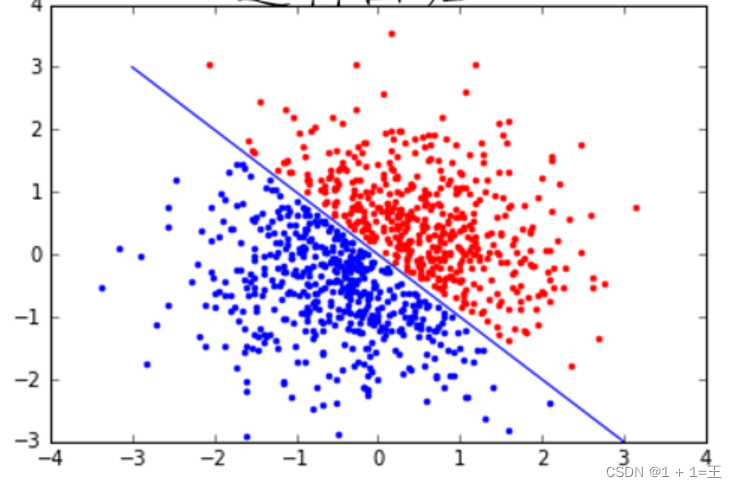
• 优点：速度快；简单易于理解，直接看到各个特征的权重；能容易地更新模型吸收新的数据。
• 缺点：特征处理复杂。需要归⼀化和较多的特征⼯程。

线性回归和逻辑回归的区别

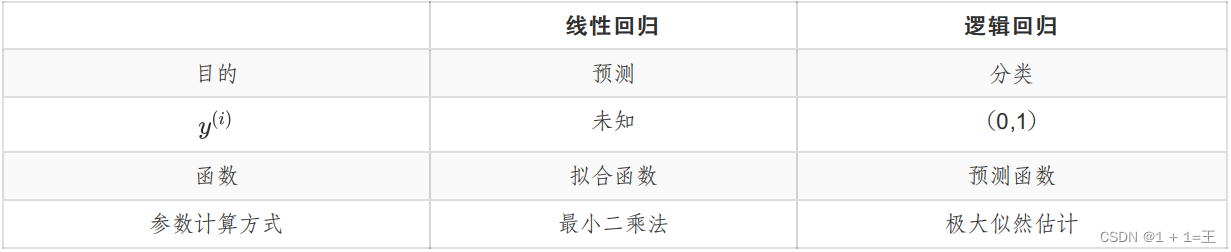
神经网络（Neural Network）

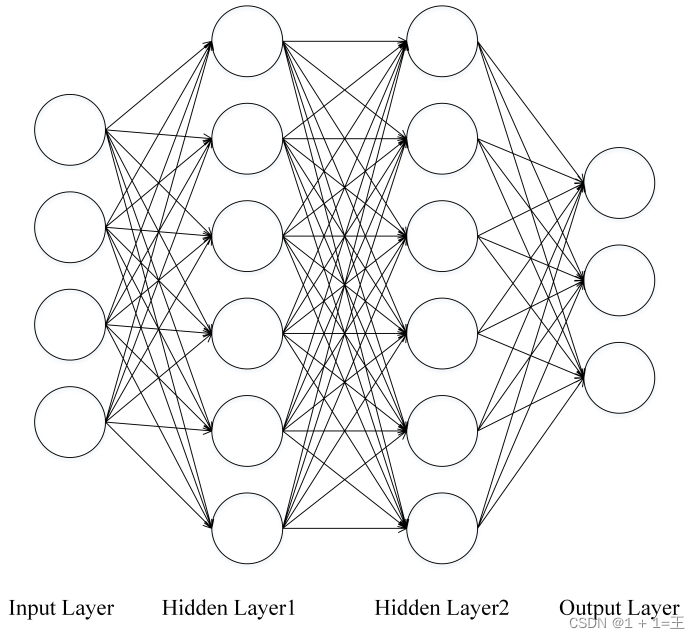
• 优点：分类准确率⾼；并⾏处理能⼒强；分布式存储和学习能⼒强；鲁棒性较强，不易受噪声影响。
• 缺点：需要⼤量参数（⽹络拓扑、阀值、阈值）；结果难以解释；训练时间过长。

Adaboosting

AdaBoosting算法是Boosting算法中最常用的一种，其思想是：先从初始训练集训练一个基学习器，在根据基学习器的表现对训练样本进行调整，使得错误的训练样本在后续受到更多关注，然后调整样本分布训练下一个基学习器；如此重复直到学习器数目达到指定值T，最终将T个学习器进行加权结合。

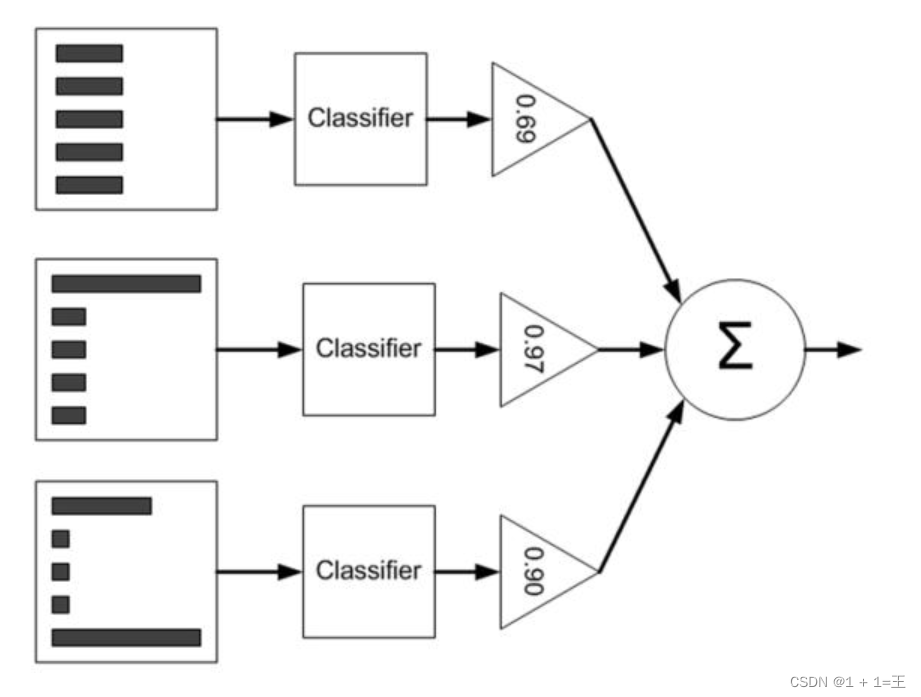
• 优点：精度高；不⽤担⼼overfitting；不⽤做特征筛选。
• 缺点：对outlier⽐较敏感

分类算法的评估⽅法

假设我们的分类⽬标只有两类，计为正例（positive）和负例（negative）分别是：

1. True positives(TP): 被正确地划分为正例的个数，即实际为正例且被分类器划分为正例的实例数；
2. False positives(FP): 被错误地划分为正例的个数，即实际为负例但被分类器划分为正例的实例数；
3. False negatives(FN):被错误地划分为负例的个数，即实际为正例但被分类器划分为负例的实例数；
4. True negatives(TN): 被正确地划分为负例的个数，即实际为负例且被分类器划分为负例的实例数。

混淆矩阵：

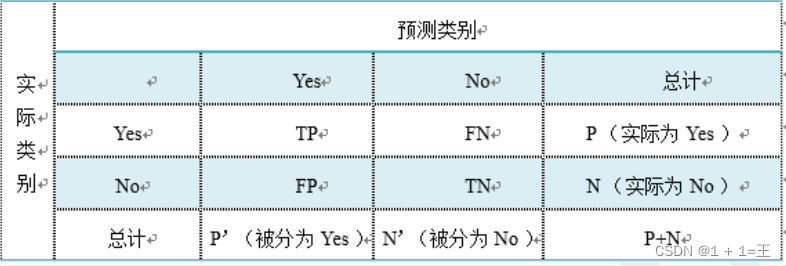
正确率（accuracy）

正确率是被分对的样本数在所有样本数中的占⽐，通常来说，正确率越⾼，分类器越好。

灵敏度（sensitivity）

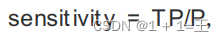
表⽰的是所有正例中被分对的⽐例，衡量了分类器对正例的识别能⼒。

特异性（specificity)

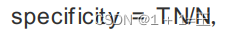
表⽰的是所有负例中被分对的⽐例，衡量了分类器对负例的识别能⼒。

精度（precision）

精度是精确性的度量，表⽰被分为正例的⽰例中实际为正例的⽐例。

召回率（recall）

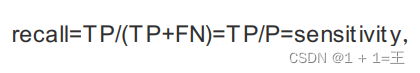
召回率是覆盖⾯的度量，度量有多个正例被分为正例。

F1-score

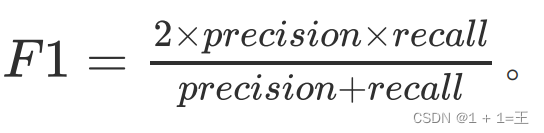
精度和召回率反映了分类器分类性能的两个⽅⾯。如果综合考虑查准率与查全率，可以得到新的评价指标F1-score。

ROC曲线

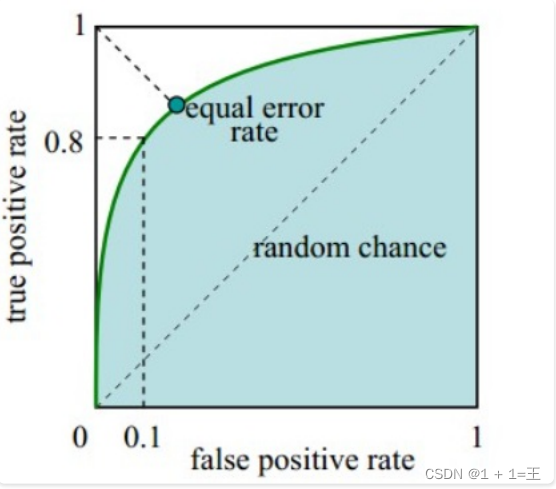
ROC曲线是（Receiver Operating Characteristic Curve，受试者⼯作特征曲线）的简称，是以灵敏度（真阳性率）为纵坐标，以1减去特异性（假阳性率）为横坐标绘制的性能评价曲线。可以将不同模型对同⼀数据集的ROC曲线绘制在同⼀笛卡尔坐标系中，ROC曲线越靠近左上⾓，说明其对应模型越可靠。也可以通过ROC曲线下⾯的⾯积（Area UnderCurve, AUC）来评价模型，AUC越⼤，模型越可靠。