一、前言

2021年12月31日，我发布了基于加权概率模型的图像滤波算法的第一个实验，当时有两个关键问题没有解决：
1、出现了大面积的黑色区域，最近考虑把这个算法实际应用在图像和视频的压缩领域，于是通过对程序的分析，发现输出时丢失了部分数据。
2、出现两点问题，在黑度图像来讲就是出现，白点和黑点问题，这个问题仅需在图像逆滤波后再修复，因为白点一定会出现在黑色区域，而黑点可以通过相邻预测的方式进行修复，下面的实验在滤波时不考虑修复问题。

今天是2023年2月20日，通过把程序做了整数化处理，并且把丢失问题整理后，我又做了一些实验，实验调用的代码如下：

int main() {
	BmpImage* img;
	const char* fileName1 = "D:\\Lena512.bmp";
	const char* fileName2 = "D:\\Lena512-mode1-15.bmp";
	unsigned char* outbuff1, * outbuff2;
	int filterRatio = 15;
	int i, count = 0, count1 = 0;
	unsigned int outlength1 = 0, length = 0;
	double h;
	// 装载BMP，并把RGB转YUV
	img = LoadBmpImage(fileName1);
	length = img->bmpInfoHeader.biWidth * img->bmpInfoHeader.biHeight;
	// 统计符号1的个数
	for (i = 0; i < length; ++i) {
		count += CntOfOneSymboltemp[img->rgbdatas->ucR[i]];
	}
	// 把灰度图像进行滤波变换
	outbuff1 = WJLFilterTransform(filterRatio, img->rgbdatas->ucR, length, &outlength1);
	if (img->rgbdatas->ucR) free(img->rgbdatas->ucR);
	for (i = 0; i < outlength1; ++i) {
		count1 += CntOfOneSymboltemp[outbuff1[i]];
	}
	// 把outbuff1进行逆滤波
	outbuff2 = WJLFilterInverseTransform(filterRatio, outbuff1, outlength1, &length);
	if (outbuff1) free(outbuff1);
	img->rgbdatas->ucR = outbuff2;
	// 又把YUV转RGB
	SaveBmpImage(fileName2, img);
	// 释放
	if (img->rgbdatas->ucR) free(img->rgbdatas->ucR);
	if (img->rgbdatas) free(img->rgbdatas);
	if (img) free(img);
	system("pause");
	// 测试图像压缩
	return 0;
}

实验采用的灰度图像为：

二、无修复部分的实验

本实验会通过几个参数设定，方便得出滤波效果以及出现了白点和黑点问题。

（2.1）实验一，filterRatio = 0

将filterRatio 设置为 0，通过编码后得出打印结果为：

从上述打印的情况可以看出，滤波是无效果的，而且字节和数据并没有变化，所以通过信息熵计算出来的压缩比几乎等于1。我采用UC进行二进制比较可以得出：

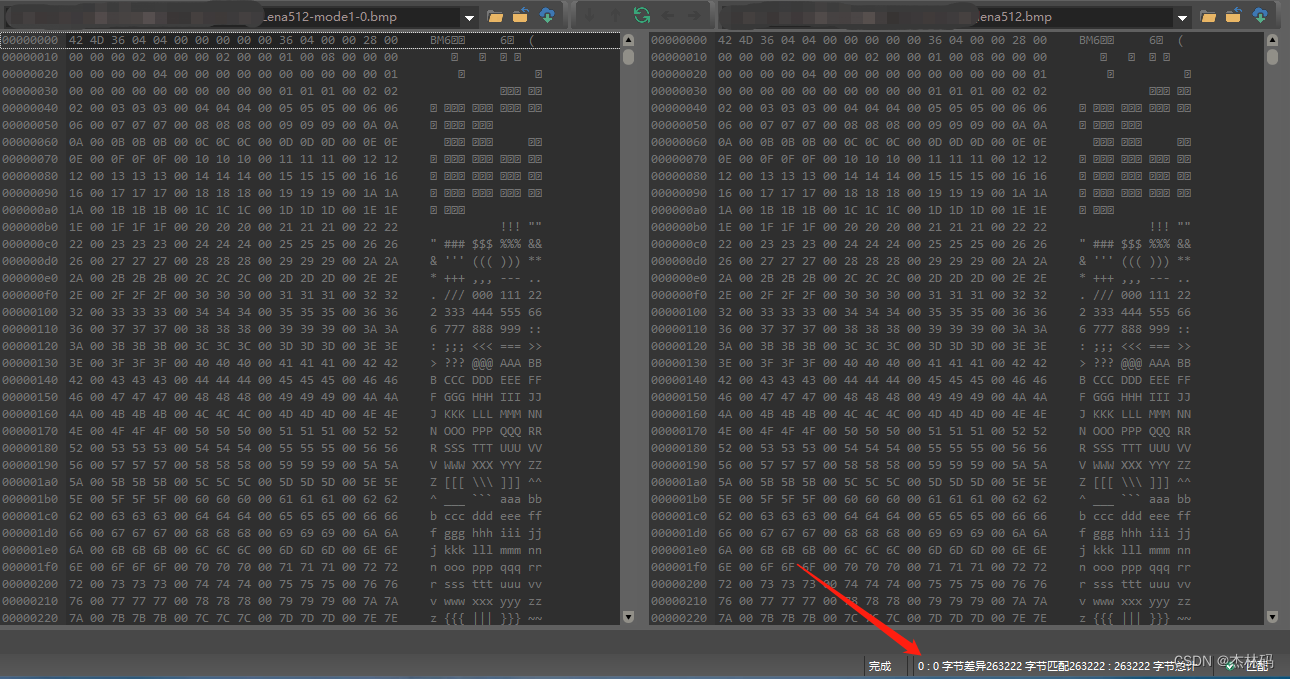
当filterRatio 设置为 0时，任何字节差错都不会出现，这个过程实际上是无滤波效果的，整个过程是无损的。

（2.2）实验二，filterRatio = 3

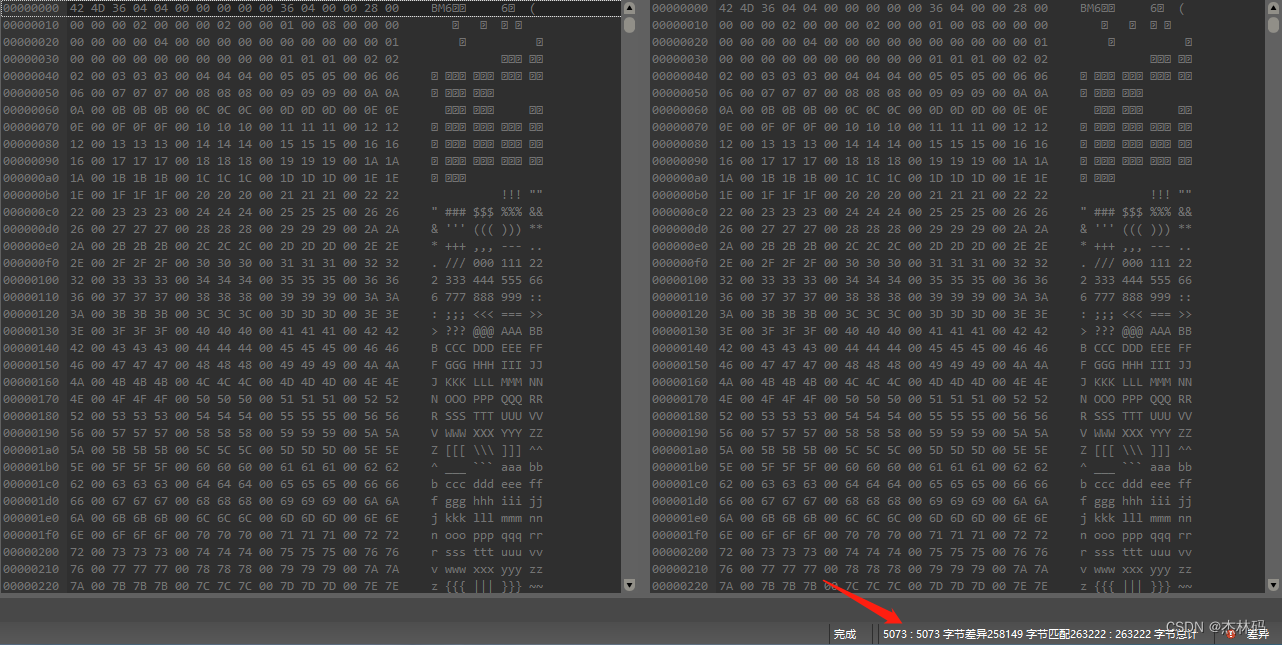
将filterRatio 设置为 3，显然，符号1的数量发生了变化，且滤波后的数据长度也发生了变化，采用二进制比较时，同样也会出现5073个字节差异。

而且滤波后的图像如下，已经在黑色区域出现白色的点，而且某些灰色区域出现了黑点：

（2.3）实验三，filterRatio = 15

将filterRatio 设置为 15此时图像为：

显然黑点和白点出现的更多了。
通过实验得出，所有的白点一定会出现在黑色区域，但是黑色的点可能出现的位置有很多，不过如果是正确的值则和原始数据一致。为了验证上述白点一定会出现在黑色区域，所以我有设计了下面的图方便验证！

三、验证白色的点一定会出现在黑色区域

实验将采用两个图来进行，一张是细胞的灰度图像，另一张是文字灰度图，分别如下：

（3.1）实验四，filterRatio = 15

得出如下效果：


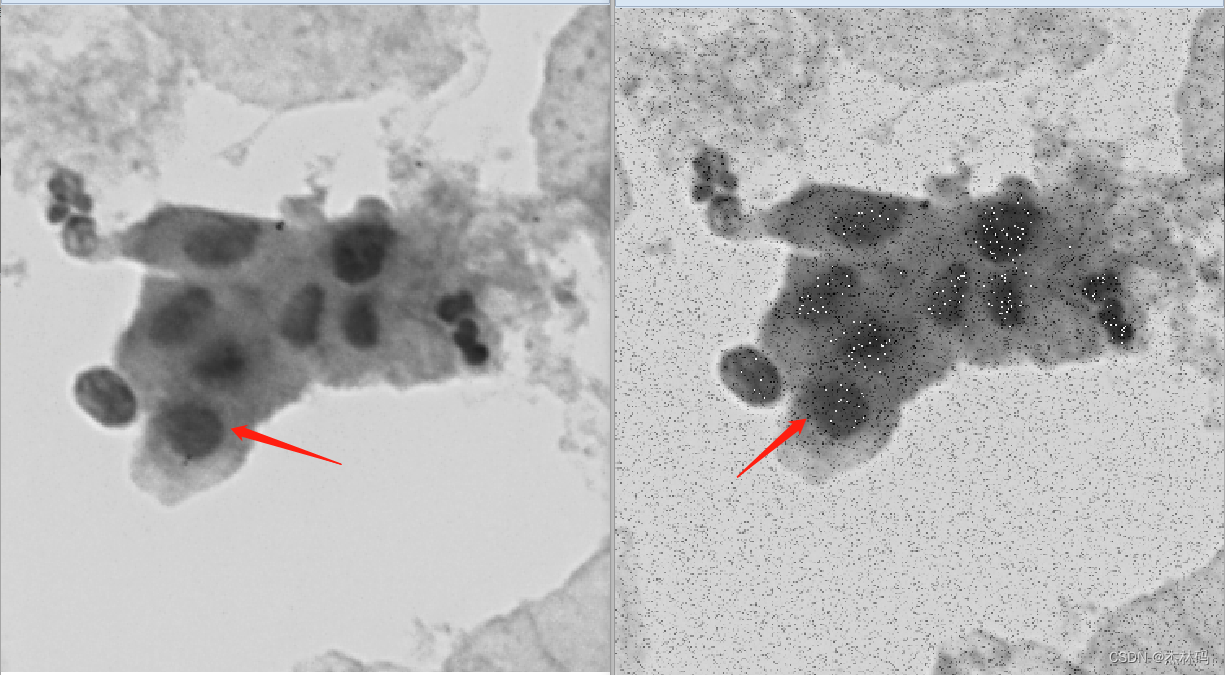
显然，白色的点一定会出现在黑色区域。

（3.2）实验五，filterRatio = 25

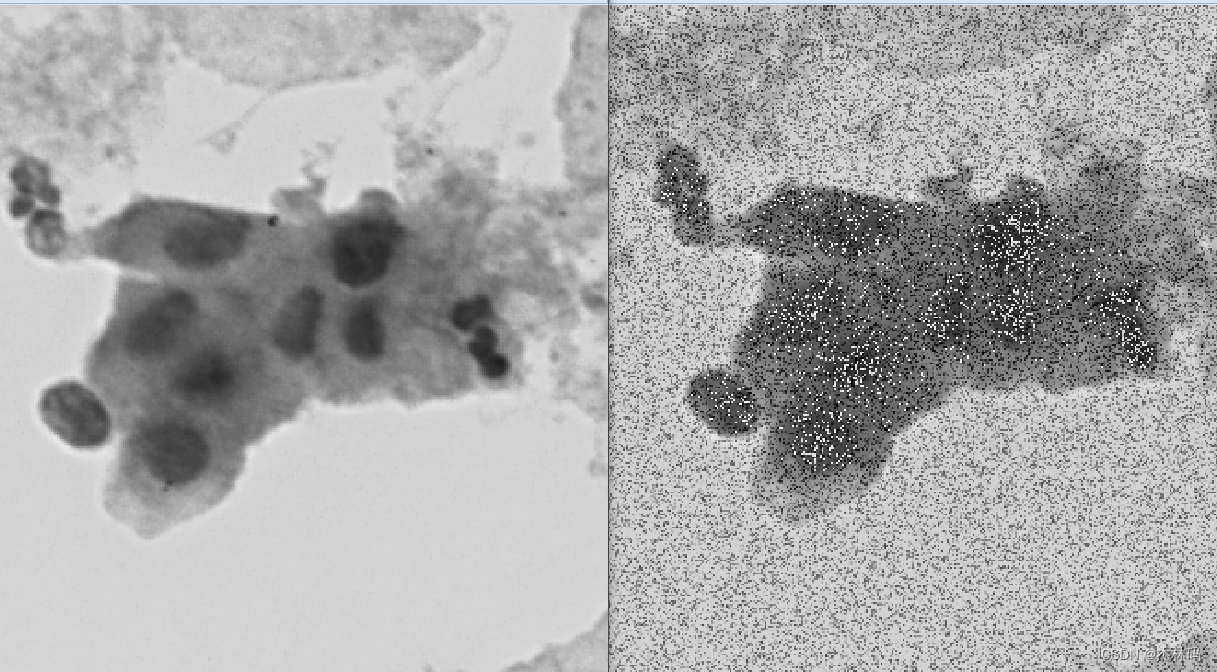
显然，这个意义非常重要，于是我又手绘了一张图，进行测试，发现可以准确的找出绘画的轨迹（filterRatio = 15）。

显然，处理滤波以外，本算法还有其他的一些意义和价值。

四、总结

通过实验不难看出，加权概率模型是可以在图像以下几个地方应用：
1、滤波，但是滤波后需要根据白点和黑点提出适合的修复方案，比如上下文差异的数值求均值填充等。
2、图像分割，通过白点必然出现在黑色区域，来针对图像进行分割，类似snake和等高线算法等，这个需要根据具体图像进行具体分析。
3、图像识别，通过对比滤波后的图和原始图，显然能得出图中的黑色文字和任意手笔迹，也就是说像素值存在下面三种情形：
设x代表的是原始值，y代表的是滤波并逆滤波后的值，于是：
（1）当y-x<t时，可以直接丢弃
（2）当y-x>=t时，则认为是当前文字或笔迹的位置，因为灰度图中黑色的值一定是接近0的值，而白色的点一定是接近255的值，另外因为白色的点一定会出现在黑色区域，所以本算法能有效的提取出图像中的文字或笔迹，然后拿这样的结果去训练识别算法即可。
4、图像锐化，显然通过上述的实验能给出图形的实际边缘，然后再通过简单的代数处理即可实现图形的边缘锐化，当然这个在某些场景下可用。
另外，filterRatio值不同，能产生的效果也不同，可以在不同的场景下设置具体的值。
（接下来的实验，我讲从上述三个方向逐步发布）