和为k的子数组

动态规划算法（超时）

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int n = nums.size();
        vector<vector<int>> dp(n, vector<int>(n, 0));
        int ans = 0;
        for(int i = 0; i < n; i++){
            dp[i][i] = nums[i];
            if(nums[i] == k) ans++;
        }
        for(int i = 0; i < n; i++){
            for(int j = i + 1; j < n; j++){
                dp[i][j] = dp[i][j-1] + nums[j];
                if(dp[i][j] == k) ans++;
            }
        }
        return ans;
    }
};

前缀和（超时）

构建前缀和数组，以快速计算区间和；

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int n = nums.size();
        vector<int> pre_sum(n + 1, 0);
        for(int i = 0; i < n; i++){
            pre_sum[i + 1] = pre_sum[i] + nums[i];
        }
        int cnt = 0;
        for(int i = 0; i <= n; i++){
            for(int j = i + 1; j <= n; j++){
                if(pre_sum[j] - pre_sum[i] == k) cnt++;
            }
        }
        return cnt;
    }
};

使用哈希表优化前缀和

用哈希表存放从数组0号元素到各个元素的和出现的次数，key表示和的值，value表示和出现的次数。哈希表存放的key表示区间[0,0]、[0,1]、[0,2]、[0,3]、[0,4]…的和

比如nums = {1,2,3}，则map中最终存放的是{{0,1},{1,1},{3,2},{6,1}}

循环累加sum的过程中，在哈希表中查找sum - k，若存在，则说明两个区间和的差为k

比如当前sum表示[0,9]区间的和，前面[0,3]、[0,5]、[0,7]区间的和是sum - k，此时mp[sum - k]是3，则说明[4,9]、[6,9]、[8,9]三个区间的和为k

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int, int> mp;
        mp[0] = 1;  // 当前和为x，k为x，差为0，则表示当前和就是k，把从0号元素到当前元素累加起来和为k的子数组记为1次
        int sum = 0;
        int ans = 0;
        for(int num : nums){
            sum += num;
            if(mp.find(sum - k) != mp.end()){
                // 当前区间和为sum，sum和前面某几个小区间和 求差为k，说明中间某个小区间的和为k
                // 比如当前sum表示[0,9]区间的和，前面[0,3]、[0,5]、[0,7]区间的和是sum - k
                // 则说明[4,9]、[6,9]、[8,9]三个区间的和为k，此时mp[sum - k]应该是3
                ans += mp[sum - k];
            }
            // mp中不断记录从0号元素到各个元素和的值出现的次数
            mp[sum]++;
        }
        return ans;
    }
};

路径总和 III

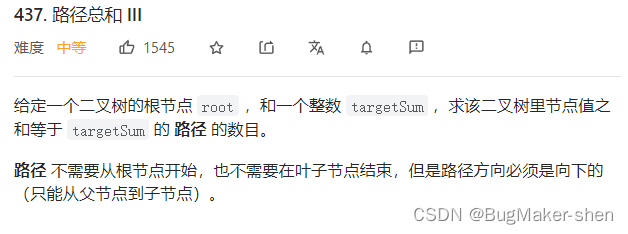
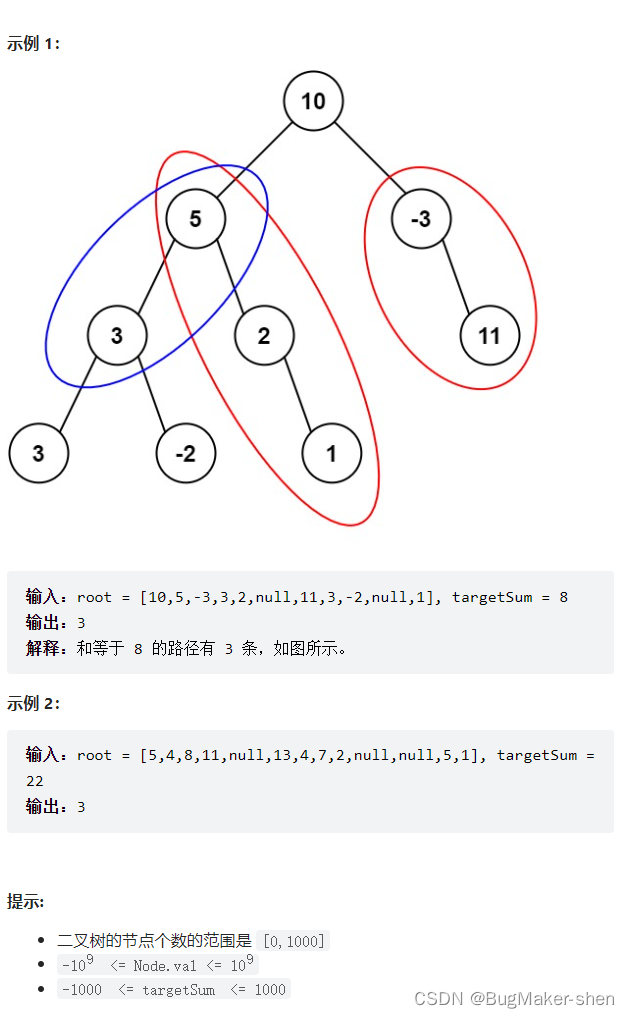
和上一题思想比较类似，哈希表记录下从根节点到每个节点的和，采用先序遍历的方式（因为每个节点需要使用到从父节点传过来的值），遍历到每个节点时，在哈希表中查找 根节点到当前节点的和 sum - target，如果存在则说明存在从根节点到某个节点的和为sum - target，即存在一段路径的和为target

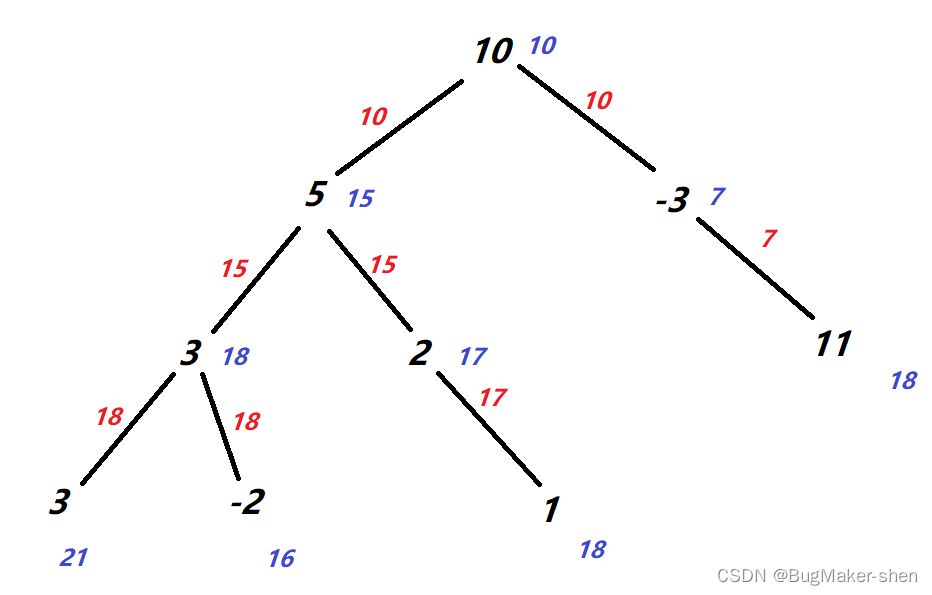
红色表示父节点给子节点传递的前缀和，紫色表示哈希表存储的前缀和（根节点到当前节点的和）

有一个需要注意的点：由于题目要求路径必须要从上到下的，不能从下到上在到下这种，也就是本题需要回溯，即代码中的mp[root->val + pre_sum]--

如果不加回溯这行代码

在遍历根节点1时，mp：{(0,1),(1,1)}

在遍历节点-2时，mp：{(0,1),(1,1),(-1,1)} ans = 1

在遍历节点-3时，mp：{(0,1),(1,1),(-1,1)} ，此时从根节点到当前节点的和sum为-2，sum - target = -1，-1在哈希表中出现了1次，而这个1次，表示从1到-2这条路径的和

sum - target = -1 ==> sum - (-1) = target

这个-1必须是sum所包含的子路径，而不应该是其他路径

所以我们遍历完某个节点，往上回溯是，需要在哈希表中当前和出现的次数 -1

class Solution {
public:
    // 哈希表中存储从根节点到各个节点的和，出现的次数
    unordered_map<long, long> mp;
    int ans;
    int target;

    // pre_sum表示从父节点传下来的和
    void dfs(TreeNode* root, long pre_sum){
        if(root == nullptr) return;
        
        // 用当前路径和root->val + pre_sum减去target，表示在map中查找是否存在某个子路径的和为root->val + pre_sum - target
        ans += mp[root->val + pre_sum - target];

        mp[root->val + pre_sum]++;
        dfs(root->left, root->val + pre_sum);
        dfs(root->right, root->val + pre_sum);
        mp[root->val + pre_sum]--;        // 当前节点遍历完成，往上回溯，从map中减去一次根节点到当前节点的和root->val + pre_sum
    }

    int pathSum(TreeNode* root, int targetSum) {
        ans = 0;
        target = targetSum;
        mp[0] = 1;
        dfs(root, 0);
        return ans;
    }
};