题目

738、单调递增的数字

给定一个非负整数 N，找出小于或等于 N 的最大的整数，同时这个整数需要满足其各个位数上的数字是单调递增。

（当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。）

示例 1:

输入: N = 10
输出: 9
示例 2:

输入: N = 1234
输出: 1234
示例 3:

输入: N = 332
输出: 299
说明: N 是在 [0, 10^9] 范围内的一个整数。

版本1
class Solution {
    public int monotoneIncreasingDigits(int N) {
        String[] strings = (N + "").split("");
        int start = strings.length;
        for (int i = strings.length - 1; i > 0; i--) {
            if (Integer.parseInt(strings[i]) < Integer.parseInt(strings[i - 1])) {
                strings[i - 1] = (Integer.parseInt(strings[i - 1]) - 1) + "";
                start = i;
            }
        }
        for (int i = start; i < strings.length; i++) {
            strings[i] = "9";
        }
        return Integer.parseInt(String.join("",strings));
    }
}

版本2
class Solution {
    public int monotoneIncreasingDigits(int n) {
        String s = String.valueOf(n);
        char[] chars = s.toCharArray();
        int start = s.length();
        for (int i = s.length() - 2; i >= 0; i--) {
            if (chars[i] > chars[i + 1]) {
                chars[i]--;
                start = i+1;
            }
        }
        for (int i = start; i < s.length(); i++) {
            chars[i] = '9';
        }
        return Integer.parseInt(String.valueOf(chars));
    }
}

714、买卖股票的最佳时机含手续费

给定一个整数数组 prices，其中第 i 个元素代表了第 i 天的股票价格 ；非负整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

示例 1:

输入: prices = [1, 3, 2, 8, 4, 9], fee = 2
输出: 8
解释: 能够达到的最大利润:

在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.
注意:

0 < prices.length <= 50000.
0 < prices[i] < 50000.
0 <= fee < 50000.

// 贪心思路
class Solution {
    public int maxProfit(int[] prices, int fee) {
        int buy = prices[0] + fee;
        int sum = 0;
        for (int p : prices) {
            if (p + fee < buy) {
                buy = p + fee;
            } else if (p > buy){
                sum += p - buy;
                buy = p;
            }
        }
        return sum;
    }
}

class Solution { // 动态规划
    public int maxProfit(int[] prices, int fee) {
        if (prices == null || prices.length < 2) {
            return 0;
        }

        int[][] dp = new int[prices.length][2];

        // base case
        dp[0][0] = 0;
        dp[0][1] = -prices[0];

        for (int i = 1; i < prices.length; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
        }

        return dp[prices.length - 1][0];
    }
}

968、监控二叉树

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：

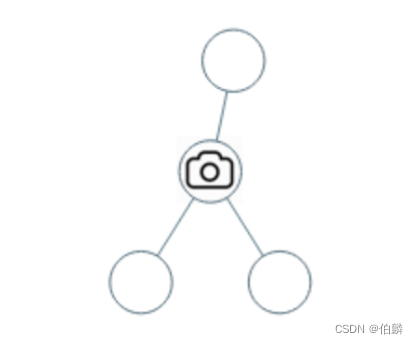
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。
示例 2：

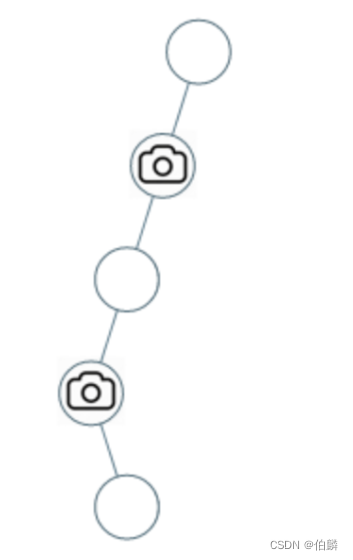
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示：

给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。

class Solution {
    int  res=0;
    public int minCameraCover(TreeNode root) {
        // 对根节点的状态做检验,防止根节点是无覆盖状态 .
        if(minCame(root)==0){
            res++;
        }
        return res;
    }
    /**
     节点的状态值：
       0 表示无覆盖 
       1 表示 有摄像头
       2 表示有覆盖 
    后序遍历，根据左右节点的情况,来判读 自己的状态
     */
    public int minCame(TreeNode root){
        if(root==null){
            // 空节点默认为 有覆盖状态，避免在叶子节点上放摄像头 
            return 2;
        }
        int left=minCame(root.left);
        int  right=minCame(root.right);
        
        // 如果左右节点都覆盖了的话, 那么本节点的状态就应该是无覆盖,没有摄像头
        if(left==2&&right==2){
            //(2,2) 
            return 0;
        }else if(left==0||right==0){
            // 左右节点都是无覆盖状态,那 根节点此时应该放一个摄像头
            // (0,0) (0,1) (0,2) (1,0) (2,0) 
            // 状态值为 1 摄像头数 ++;
            res++;
            return 1;
        }else{
            // 左右节点的 状态为 (1,1) (1,2) (2,1) 也就是左右节点至少存在 1个摄像头，
            // 那么本节点就是处于被覆盖状态 
            return 2;
        }
    }
}