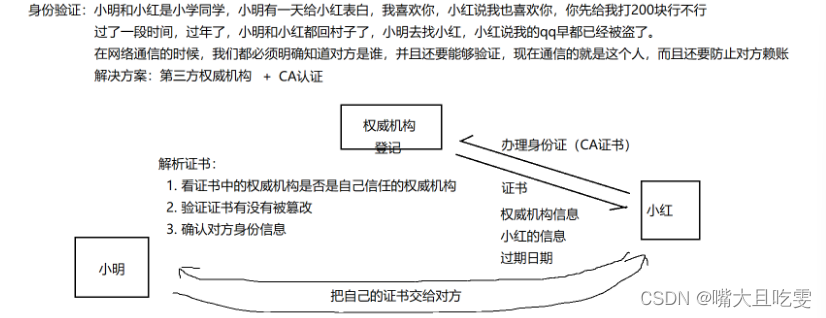
这道题目核心的一行代码就是判断s1的第i个字符和s2的第j个字符是否相等

是s1.charAt(i-1)==s2.charAt(j-1)

而不是s1.charAt(i)===s2.charAt(j)

动态规划就是搞清楚dp[i][j]的含义然后写出动态转移方程

(1)dp[i][j]的含义

dp[i][j]表示考虑s1的前i个字符，考虑s2的前j个字符，得到的最长公共子序列的长度

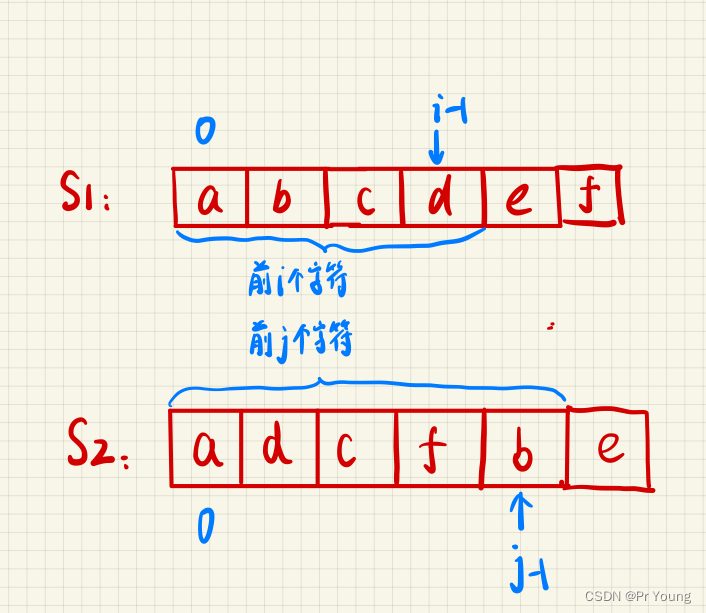
 下图就表示dp[4][5]=2

(2)动态转移方程

当s1.charAt(i-1)==s2.charAt[j-1]的时候，s1第i个字符等于s2第j个字符

dp[i][j]=dp[i-1][j-1]+1

当s1.charAt(i-1)!=s2.charAt[j-1]的时候,dp[i][j]=max(dp[i][j-1],dp[i-1][j])   

i，j向前各走1步，等于max(i向前走1步而且j不动，i不动而且j向前走1步)

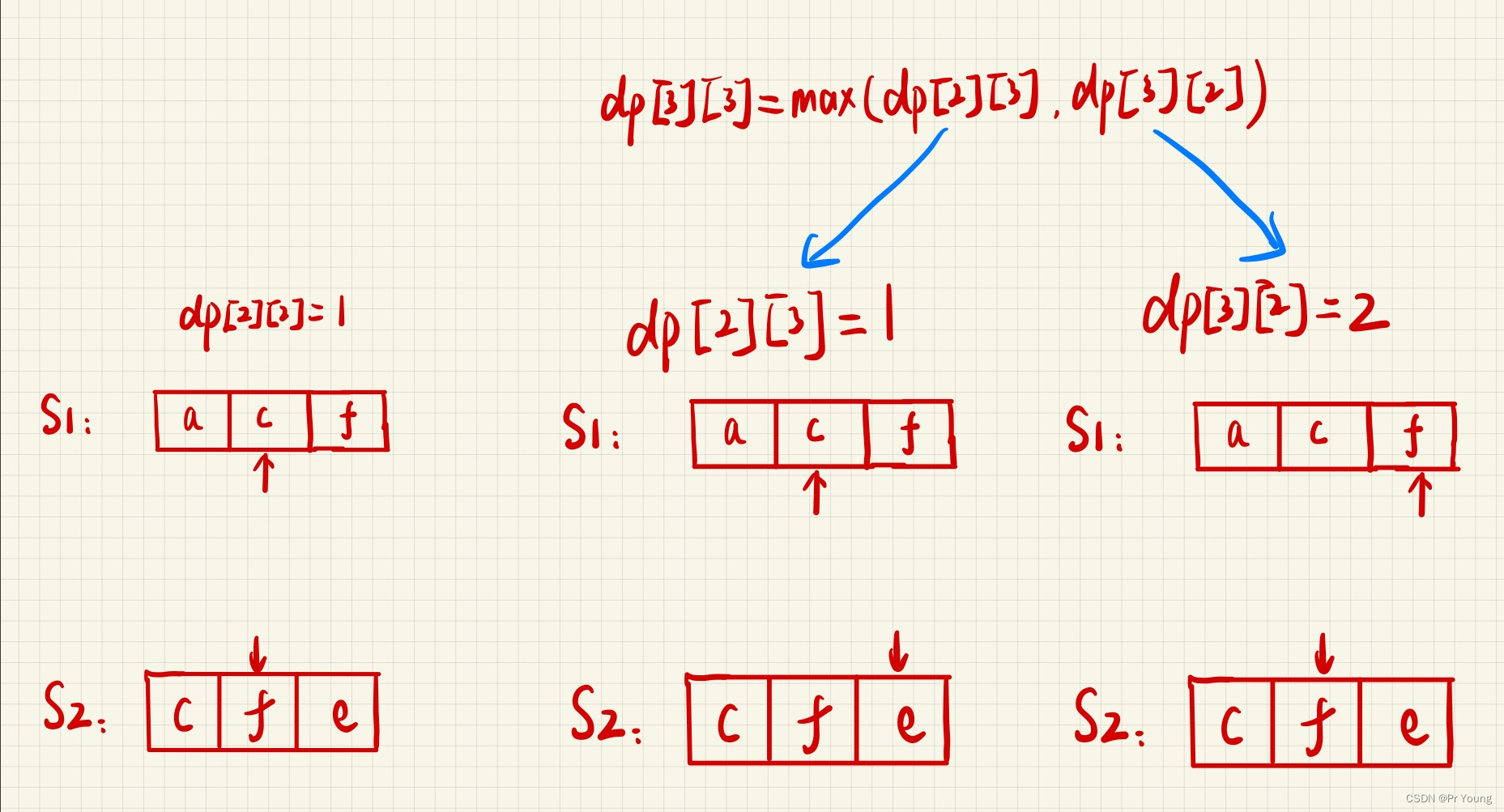
下图演示了如何由dp[2][2]得到dp[3][3]

 注意这里：

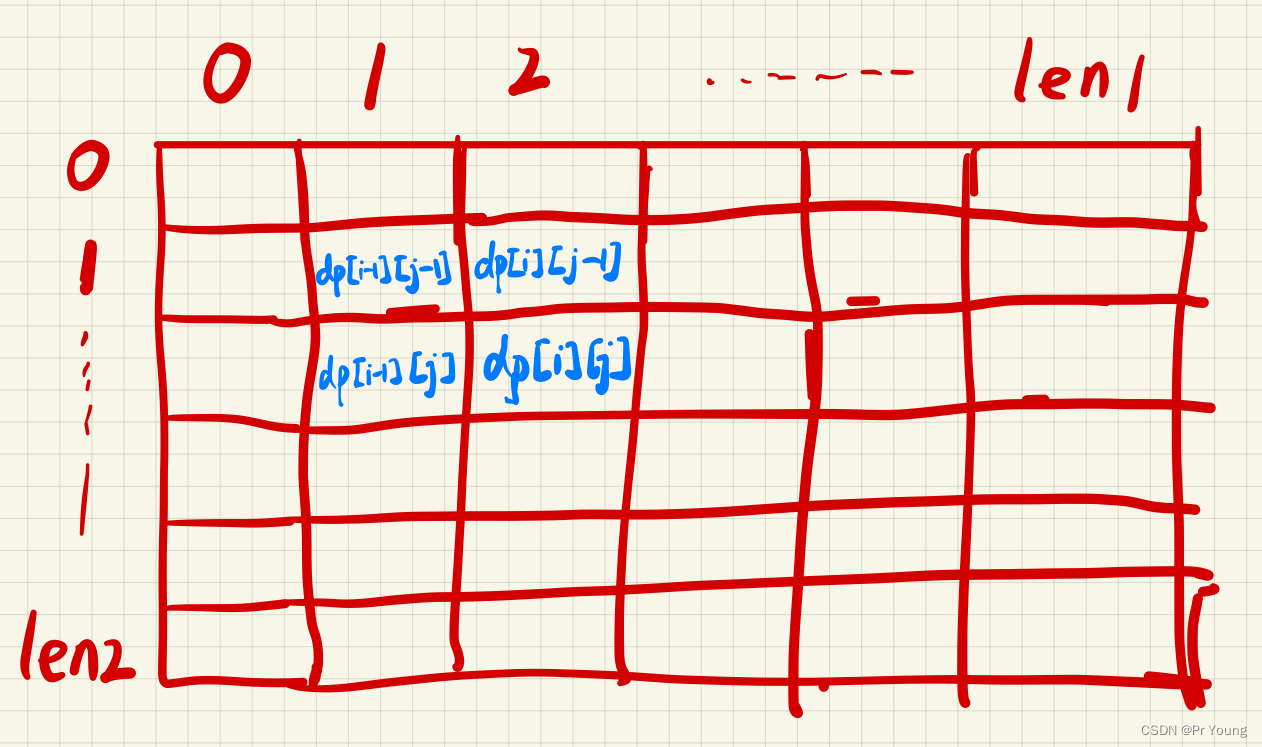
(1)dp[i][j]表示考虑s1前i个字符，考虑s2前j个字符

求dp[i][j]需要根据dp[i-1][j-1]或者dp[i][j-1]+dp[i-1][j]

 (2)判断s1第i个字符和s2第j个字符是否相等：是s1.charAt(i-1)==s2.charAt(j-1)

而不是s1.charAt(i)===s2.charAt(j)

class Solution
{
    public int longestCommonSubsequence(String text1, String text2)
    {
        int len1=text1.length();
        int len2=text2.length();
        int[][] dp=new int[len1+1][len2+1];
        

        for(int i=1;i<=len1;i++)
        {
            for(int j=1;j<=len2;j++)
            {
                if(text1.charAt(i-1)==text2.charAt(j-1))
                {
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                else
                {
                    dp[i][j]=Math.max(dp[i][j-1],dp[i-1][j]);
                }
            }
        }
        
        return dp[len1][len2];
    }
}