第k小的元素

🔒题目

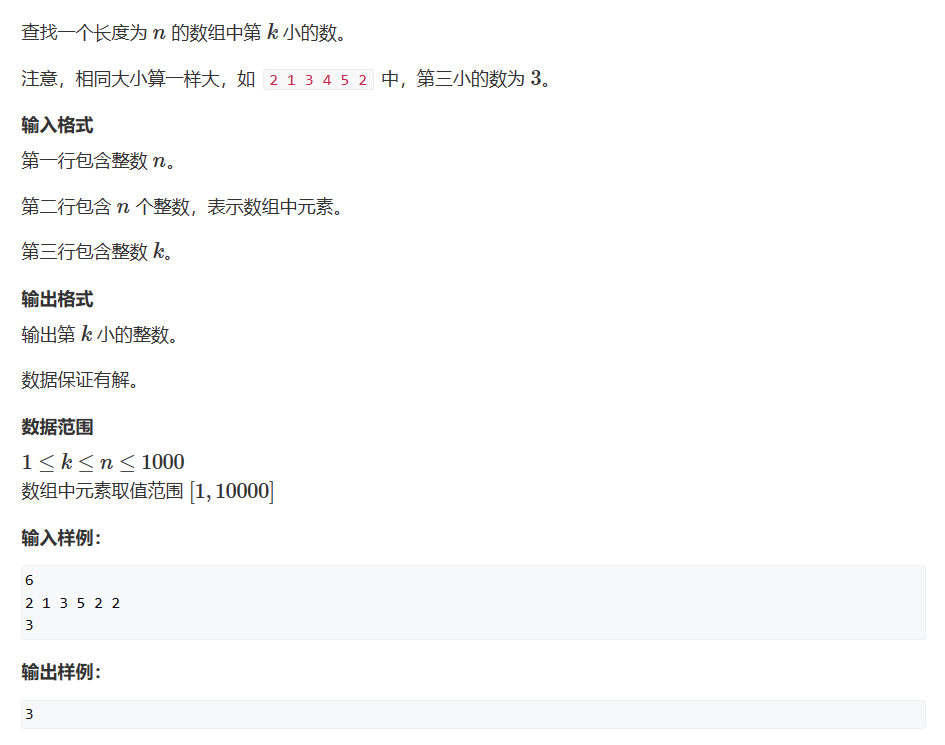
题目来源：3533. 查找第K小数 - AcWing题库

💡分析

不去重版思路：
去重版思路：

🔑题解

🍃不去重版

只能对于非重复元素的数组才有效，对于出现了重复元素的数组并不能得到正确答案，所以还需要改进

方式一：采用快速排序策略，核心思想**分治+递归**

时间复杂度： $O (n l o g n)$ ，n为数组中元素的个数

import java.util.Scanner;

/**
 * @author ghp
 * @title 求第k小的元素（不去重版）
 * @description 通过快速排序策略得到数组中第k小的数
 */
public class Main {
	public static void main(String[] args) {
		// 接收输入
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int[] arr = new int[n];
		for (int i = 0; i < n; i++) {
			arr[i] = sc.nextInt();
		}
		int k = sc.nextInt(); // 第k小
		// 通过快速排序查找到第k小的数
		int result = findKthByQuickSort(arr, 0, arr.length - 1, k);
		// 输出第k小的数
		System.out.println(result);
	}

	/**
	 * 通过快速排序查找第k小的数
	 * @param arr 待查找的数组
	 * @param left 待查找数组的左侧索引
	 * @param right 待查找数组的右侧索引
	 * @param k 第k小
	 * @return 返回第k小的数，arr中不含有则返回-1
	 */
	private static int findKthByQuickSort(int[] arr, int left, int right, int k) {
		if(left>right) {
			// 未找到要查找的数，返回-1，递归终止
			return -1;
		}
		// 获取主元
		int pivot = partition(arr, left, right);
		int result; // 第k小的元素
		if (k == pivot - left + 1) {
			// 第k小的元素就是当前子数组的主元
			result = arr[pivot];
		} else if (k < pivot - left + 1) {
			// 第k小的元素在主元左侧
			result = findKthByQuickSort(arr, left, pivot - 1, k);
		} else {
			// 第k小的元素在主元右侧
			result = findKthByQuickSort(arr, pivot + 1, right, k - (pivot - left + 1));
		}
		// 返回第k小的数
		return result;
	}

	/**
	 * 根据主元划分数组（左侧子数组恒小于等于主元，右侧子数组恒）
	 * @param arr 待划分的数组
	 * @param left 待划分数组的左侧索引
	 * @param right 待划分数组的右侧索引
	 * @return 返回本次用于划分数组的主元
	 */
	private static int partition(int[] arr, int left, int right) {
		int pivot = arr[right]; // 主元
		int i = left - 1; // 左右子数组的分界点
		// 遍历arr，然后根据主元划分出两个子数组
		for (int j = left; j <= right - 1; j++) {
			// 将比主元小的数组放到i+1的左侧（注意: i+1也比主元小）
			if (arr[j] < pivot) {
				int tmp = arr[i + 1];
				arr[i + 1] = arr[j];
				arr[j] = tmp;
				i++;
			}
		}
		// 将主元放到分界点
		int temp = arr[i + 1];
		arr[i + 1] = arr[right];
		arr[right] = temp;
		// 返回主元索引
		return i + 1;
	}
}

方式二：调用Java的API，主要思路，先去重，然后通过Arrays.sort()方法进行排序

时间复杂度： $O (n l o g n)$ ，n为数组中元素的个数

import java.util.Arrays;
import java.util.Scanner;

/**
 * @author ghp
 * @title 求第k小的元素
 * @description
 */
public class Main {
	public static void main(String[] args) {
		// 接收输入
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int[] arr = new int[n];
		for (int i = 0; i < n; i++) {
			arr[i] = sc.nextInt();
		}
		int k = sc.nextInt(); // 第k小
		// 去除重复元素
		Arrays.sort(arr);
		// 输出第k小的数
		System.out.println(arr[k-1]);
	}
}

🍃去重版

方式一：利用Set集合的特性

核心思想是利用Set集合的特性

Set集合中的元素不可重复
Set集合中的元素默认是升序排序的

时间复杂度： $O (n)$

import java.util.Arrays;
import java.util.HashSet;
import java.util.Scanner;
import java.util.Set;

/**
 * @author ghp
 * @title 求第k小的元素
 * @description
 */
public class Main {
	public static void main(String[] args) {
		// 接收输入
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int[] arr = new int[n];
		for (int i = 0; i < n; i++) {
			arr[i] = sc.nextInt();
		}
		int k = sc.nextInt(); // 第k小
		// 去除重复元素
		int[] nums = Arrays.stream(removeRepeat(arr))
				.mapToInt(Integer::valueOf).toArray();
		// 输出第k小的数
		System.out.println(arr[k-1]);
	}

	/**
	 * 去除重复元素
	 * @param arr
	 * @return
	 */
	private static Integer[] removeRepeat(int[] arr) {
		Set<Integer> set = new HashSet<>();
		for (int i = 0; i < arr.length; i++) {
			set.add(arr[i]);
		}
		return set.toArray(new Integer[set.size()]);
	}
}