【深度学习编译器系列】2. 深度学习编译器的通用设计架构

news2025/2/26 21:55:09

在【深度学习编译器系列】1. 为什么需要深度学习编译器？中我们了解到了为什么需要深度学习编译器，和什么是深度学习编译器，接下来我们把深度学习编译器这个小黑盒打开，看看里面有什么东西。

1. 深度学习编译器的通用设计架构

与传统编译器类似，深度学习编译器也采用分层设计。深度学习编译器主要包括编译器前端和编译器后端两部分。

编译器前端主要执行硬件无关的转换和优化，如算子融合，布局转换，代数化简等。
编译器后端主要执行硬件相关的优化，如内核库调用，自动调优，内存分配等。
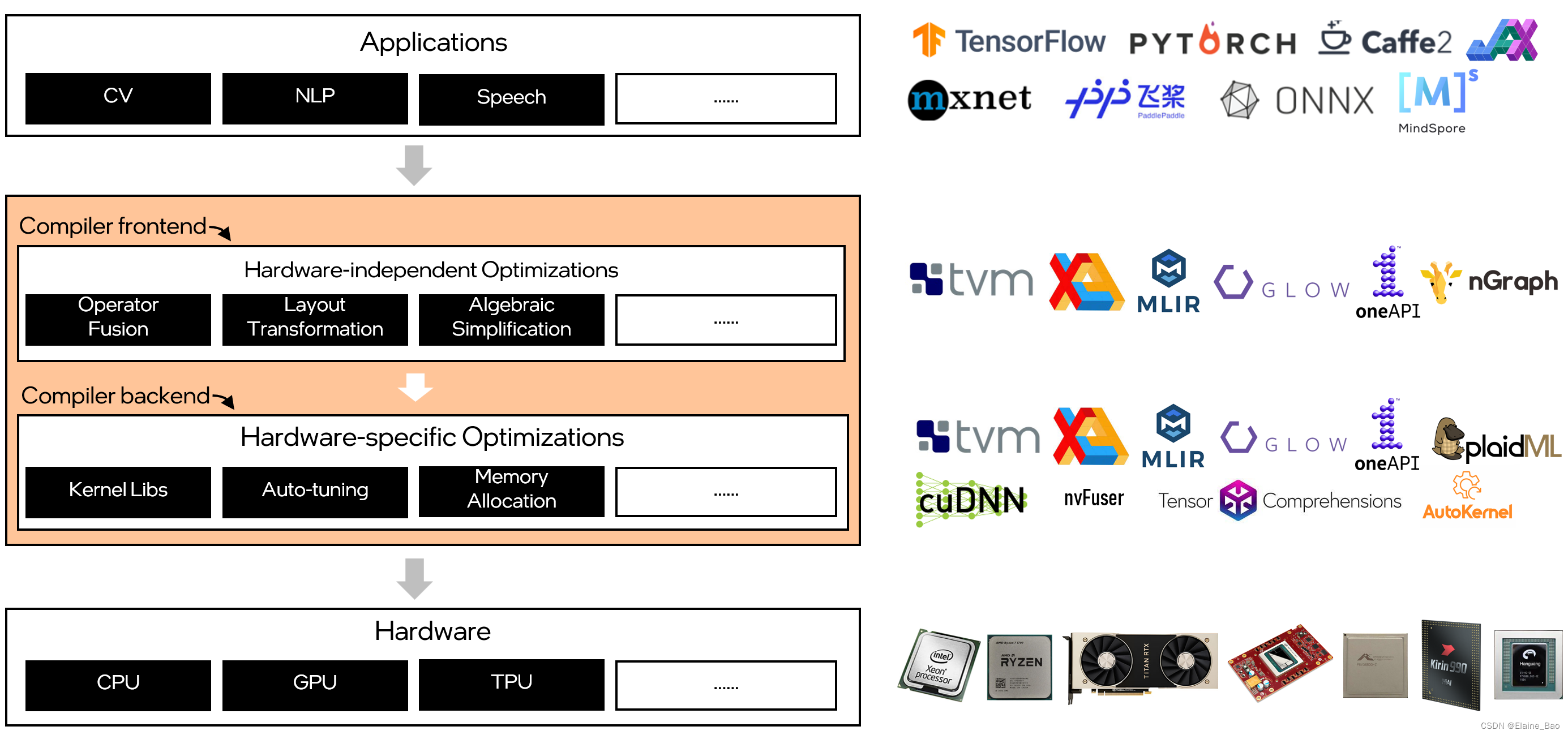
DLC Architecture
另外，深度学习编译器还有一个必不可少的部分，在上图中没有显式表示出来的，就是中间表示 (intermediate representation, IR)。
IR贯穿深度学习编译器的整个架构，首先深度学习模型通过high level IR（也称为计算图IR）翻译到编译器的前端，编译器前端基于高阶IR进行一系列优化。然后high level IR再映射到编译器后端的low level IR (operator IR)，编译器后端基于low level IR进行一系列优化、代码生成和编译。

2. 深度学习编译器的入局者

在深度学习编译器的整个软件栈上，目前有非常多的玩家在持续投入。从应用层面来看有很多成熟的深度学习框架，如Tensorflow, Pytorch等。从硬件层面来看也不断有各种深度学习专用芯片的产生，如Google的TPU，Nvidia的Turing，Intel NNP，Amazon的Inferentia，阿里平头哥的含光，华为海思的NPU等。从深度学习编译器本身，工业界和学术界也推出了不同的深度学习编译器，比如TVM，TensorFlow XLA，Pytorch NvFuser，Intel nGraph，Google MLIR等。不同的玩家侧重点也不同，有的侧重于前端优化，有的侧重于后端优化。

总的来说，深度学习编译器这个领域看起来正处于百家争鸣的时候，这让人不禁想起了上世纪90年代，传统编译器遍地开花的场景。那么未来，深度学习编译器是否会像传统编译器一样收敛到一个比较统一的范式（GCC/LLVM）呢？让我们拭目以待一下。