0 建议学时
4学时
1 人工智能概述
2020中国人工智能产业年会在苏州召开,会上发布的《中国人工智能发展报告2020》显示,过去十年(2011-2020) ,中国人工智能专利申请量达389571件,占全球总量的74.7%,位居世界第一。
报告指出,中国在自然语言处理、芯片技术、机器学习等10多个人工智能子领域的科研产出水平居于世界前列。

人工智能被认为是二十一世纪三大尖端技术(基因工程、纳米科学、人工智能)之一。
人工智能的基石是数学,而这些数学算法的实现是由一个一个的函数组合得来。比如,我们计算
sin
(
π
h
r
2
)
\sin (\pi hr^2)
sin(πhr2) 可以得到圆柱体的体积的正弦值。对于前述公式,我们就可以将其分解为3个简单的乘法和一个正弦函数。在编程语言中,我们也把这些函数称为方法。目前流行的人工神经网络,实际上就是由几百甚至几千个方法构成。通过定义方法不仅可以实现简单的数学公式,还可以实现一些无法用数学公式描述的算法,如遗传算法。人工智能的三大要素:
- 数据
- 算法
- 算力
2 遗传算法
一种通过模拟自然进化过程搜索最优解的方法。遗传算法是一种仿生算法,最主要的思想是物竞天择,适者生存。这个算法很好的模拟了生物的进化过程,保留好的物种,同样一个物种中的佼佼者才会幸运的存活下来。转换到数学问题中,这个思想就可以很好的转化为优化问题,在求解方程组的时候,好的解视为好的物种被保留,坏的解视为坏的物种而淘汰,设置好进化次数以后开始迭代,记录下这些解里面最好的那个,就是要求解的方程组的解。
遗传算法是类比自然界的达尔文进化实现的简化版本。
达尔文进化论的原理概括总结如下:
- 变异:种群中单个样本的特征(性状,属性)可能会有所不同,这导致了样本彼此之间有一定程度的差异;
- 遗传:某些特征可以遗传给其后代。导致后代与双亲样本具有一定程度的相似性;
- 选择:种群通常在给定的环境中争夺资源。更适应环境的个体在生存方面更具优势,因此会产生更多的后代。
2.1 基本概念
2.1.1 基因和染色体

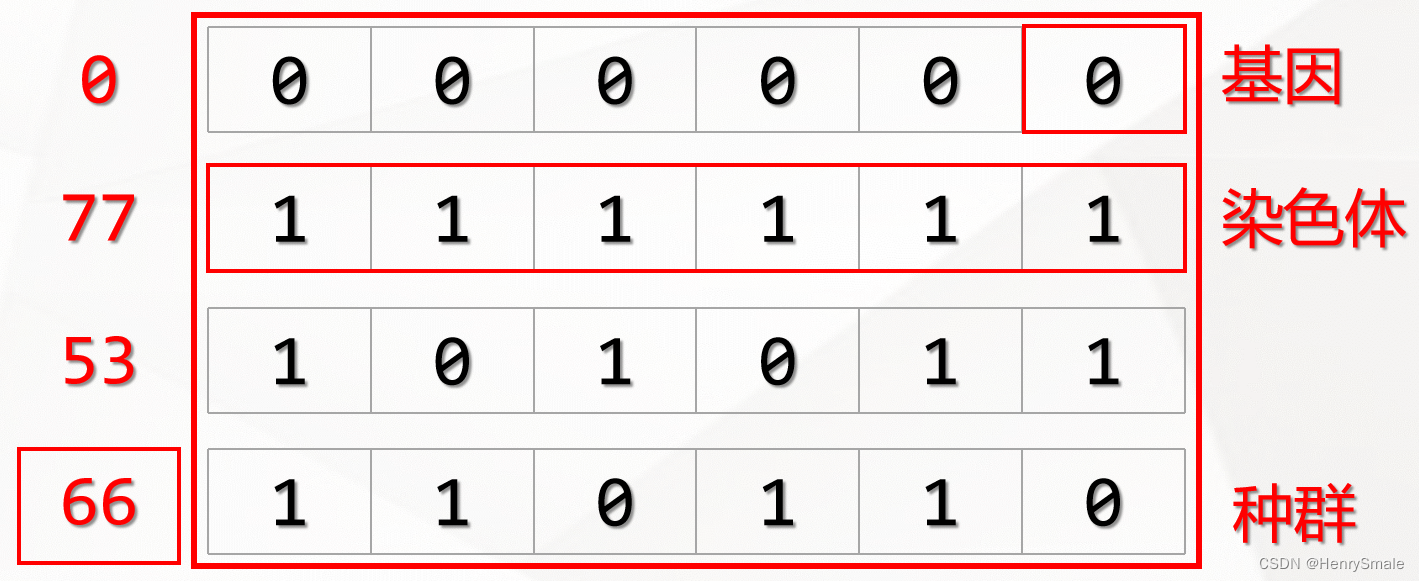
在遗传算法中,我们首先需要将要解决的问题映射成一个数学问题,也就是所谓的“数学建模”,那么这个问题的一个可行解即被称为一条“染色体”。一个可行解一般由多个元素构成,那么这每一个元素就被称为染色体上的一个“基因”。
比如说,对于如下函数而言,[1,2,3]、[1,3,2]、[3,2,1]均是这个函数的可行解(代进去成立即为可行解),那么这些可行解在遗传算法中均被称为染色体。
3
x
+
4
y
+
5
z
<
100
3x+4y+5z<100
3x+4y+5z<100
这些可行解一共有三个元素构成,那么在遗传算法中,每个元素就被称为组成染色体的一个基因。
2.1.2 适应度函数
在自然界中,似乎存在着一个上帝,它能够选择出每一代中比较优良的个体,而淘汰一些环境适应度较差的个人。那么在遗传算法中,如何衡量染色体的优劣呢?这就是由适应度函数完成的。适应度函数在遗传算法中扮演者这个“上帝”的角色。
遗传算法在运行的过程中会进行N次迭代,每次迭代都会生成若干条染色体。适应度函数会给本次迭代中生成的所有染色体打个分,来评判这些染色体的适应度,然后将适应度较低的染色体淘汰掉,只保留适应度较高的染色体,从而经过若干次迭代后染色体的质量将越来越优良。
2.1.3 交叉
遗传算法每一次迭代都会生成N条染色体,在遗传算法中,这每一次迭代就被称为一次“进化”。那么,每次进化新生成的染色体是如何而来的呢?——答案就是“交叉”,你可以把它理解为交配。
交叉的过程需要从上一代的染色体中寻找两条染色体,一条是爸爸,一条是妈妈。然后将这两条染色体的某一个位置切断,并拼接在一起,从而生成一条新的染色体。这条新染色体上即包含了一定数量的爸爸的基因,也包含了一定数量的妈妈的基因。
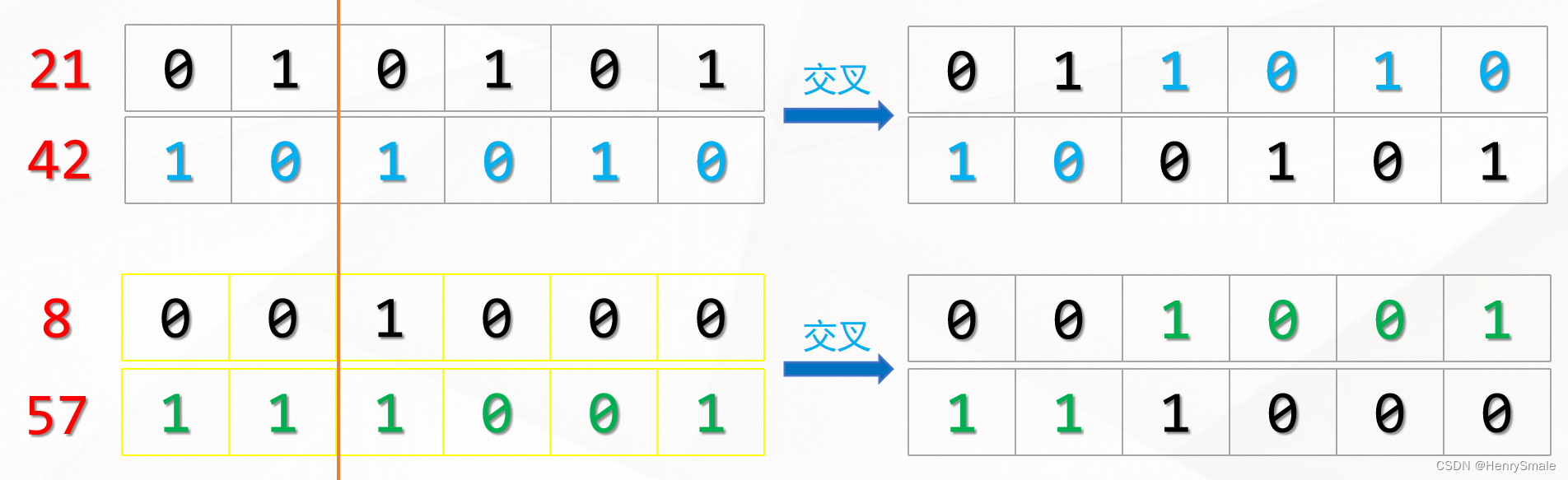
那么,如何从上一代染色体中选出爸爸和妈妈的基因呢?这不是随机选择的,一般是通过轮盘赌算法完成。
在每完成一次进化后,都要计算每一条染色体的适应度,然后采用如下公式计算每一条染色体的适应度概率。那么在进行交叉过程时,就需要根据这个概率来选择父母染色体。适应度比较大的染色体被选中的概率就越高。这也就是为什么遗传算法能保留优良基因的原因。
染色体i被选择的概率 = 染色体i的适应度 / 所有染色体的适应度之和
2.1.4 变异
交叉能保证每次进化留下优良的基因,但它仅仅是对原有的结果集进行选择,基因还是那么几个,只不过交换了他们的组合顺序。这只能保证经过N次进化后,计算结果更接近于局部最优解,而永远没办法达到全局最优解,为了解决这一个问题,我们需要引入变异。
变异很好理解。当我们通过交叉生成了一条新的染色体后,需要在新染色体上随机选择若干个基因,然后随机修改基因的值,从而给现有的染色体引入了新的基因,突破了当前搜索的限制,更有利于算法寻找到全局最优解。

2.1.5 复制
每次进化中,为了保留上一代优良的染色体,需要将上一代中适应度最高的几条染色体直接原封不动地复制给下一代。
假设每次进化都需生成
N
N
N条染色体,那么每次进化中,通过交叉方式需要生成
N
−
M
N-M
N−M条染色体,剩余的
M
M
M条染色体通过复制上一代适应度最高的M条染色体而来。
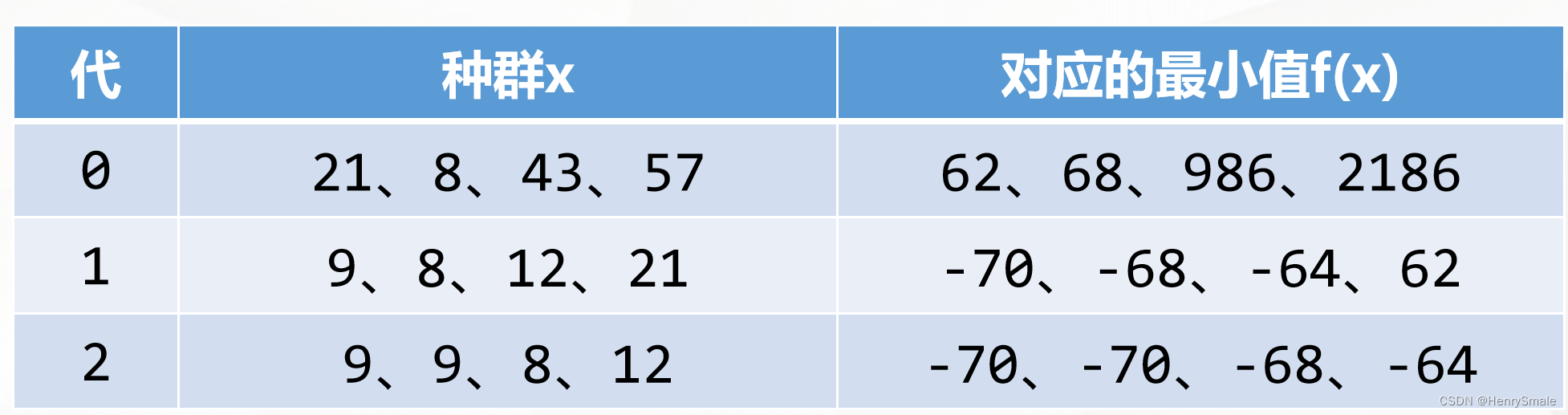
2.2 通过例子说明进化过程
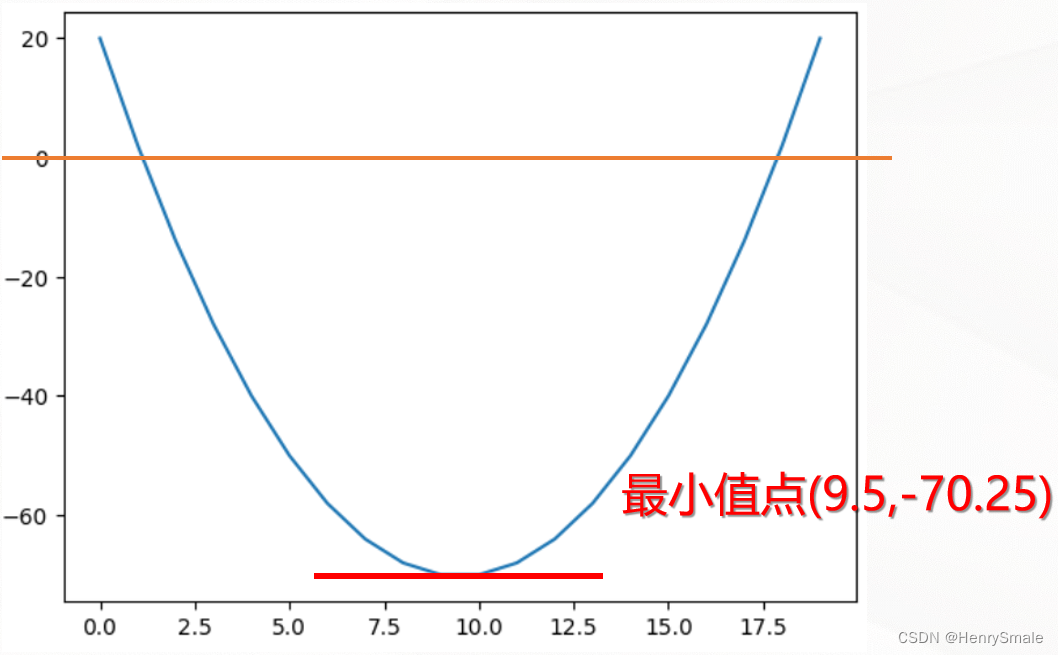
求 f ( x ) = x 2 − 19 x + 20 f(x)=x^2-19x+20 f(x)=x2−19x+20的最小值,其中 x = 1 , … , 64 x=1,…,64 x=1,…,64之间的整数。
2.2.1 第一轮
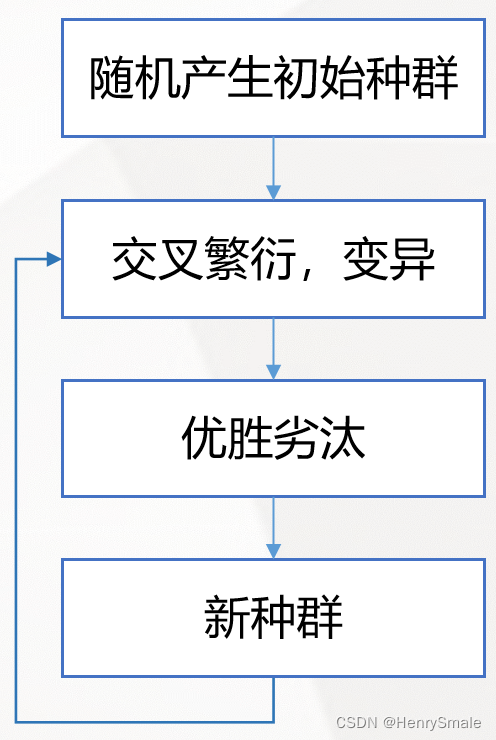
随机产生初始种群
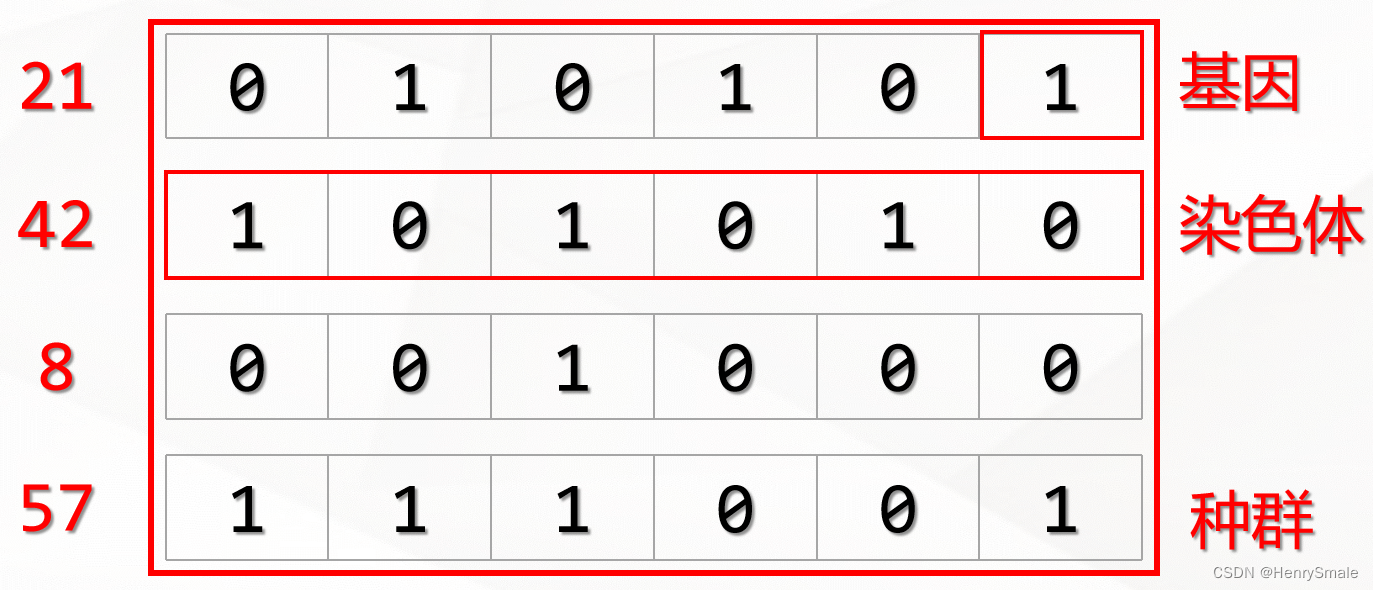
交叉繁衍,变异
优胜劣汰

流程图
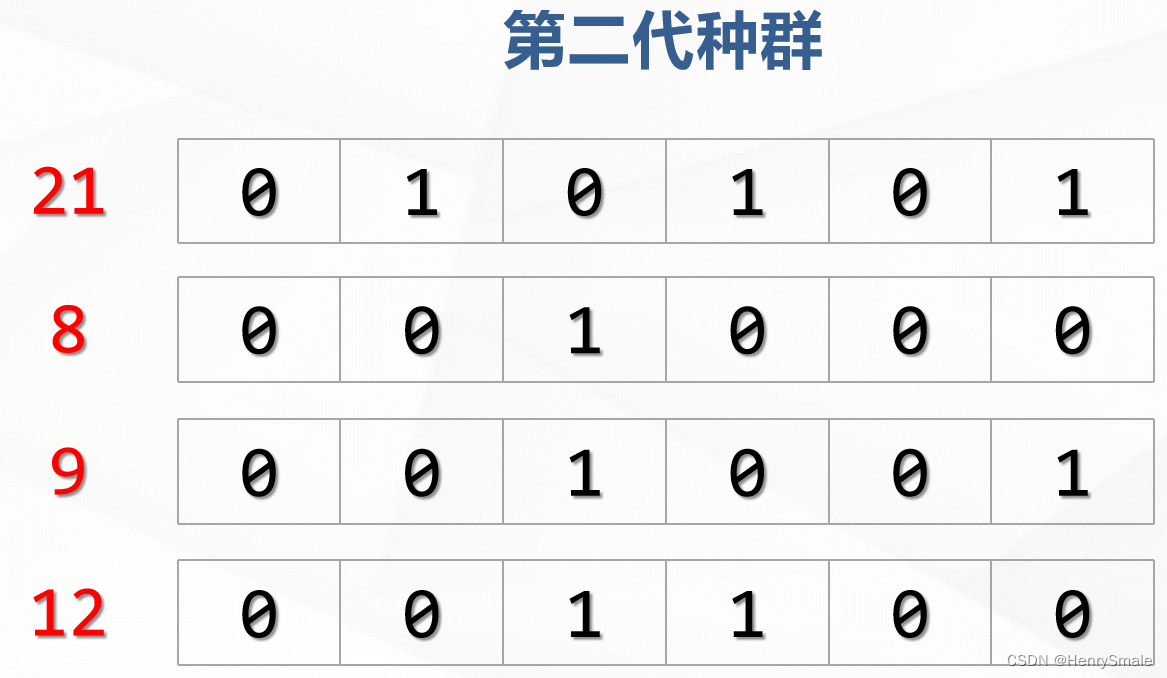
2.2.2 第二轮
交叉繁衍,变异
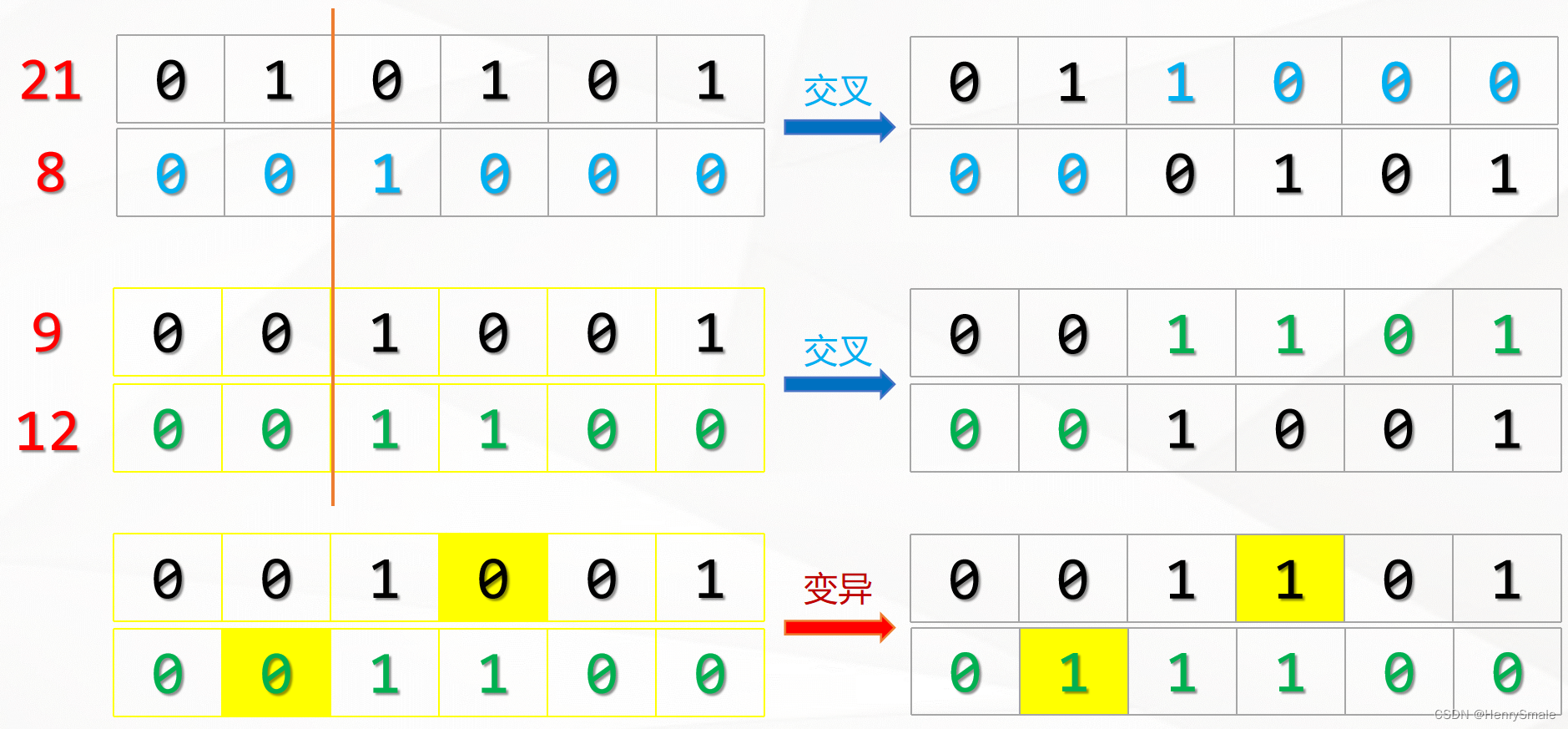
优胜劣汰

3 如何编写<遗传算法计算最小值>的程序?
根据流程图写出步骤,每个步骤标号:
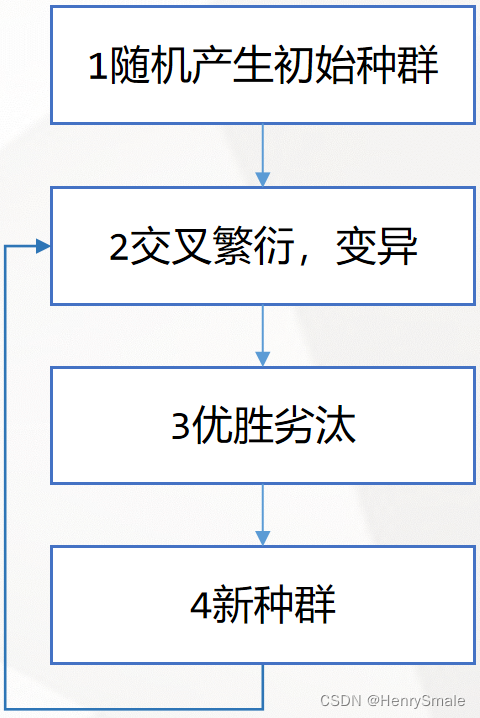
细化所有的步骤,直到能和代码对应为止。
如何设计函数?哪些代码应该封装为函数?
3.1 基础知识回顾
- 复习1:函数定义
def fact(n):
s = 1
for i in range(1, n+1):
s*= i
return s
- 复习2:函数调用
a=fact(5)
print(a)
- 复习3:匿名函数

sum = lambda a,b: a+b
print(sum(1 , 3)) #调用函数打印其返回值
3.2 模块设计
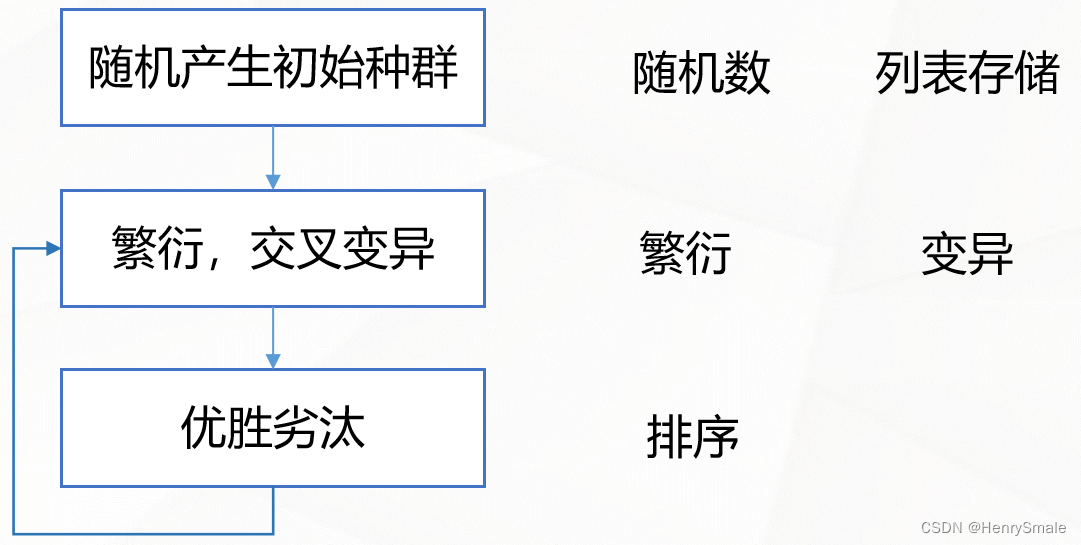
3.3 核心代码
3.3.1 随机产生初始种群
lt=[21,42,8,57]
3.3.2 繁衍,交叉变异

# 繁衍,交换基因,x,y是数据,pos是从第几位开始交换
def exchange(x, y, pos):
xstr = '{0:06b}'.format(x) # 转换为6位二进制
ystr = '{0:06b}'.format(y) # 转换为6位二进制
tempxstr = '0b' + xstr[:pos] + ystr[pos:] # 临时存放
tempystr = '0b' + ystr[:pos] + xstr[pos:] # 临时存放
return int(tempxstr, 2), int(tempystr, 2) # 再转换为十进制

# 交叉变异
def mutate(x, pos):
xstr = '{0:06b}'.format(x) # 转换为6位二进制
if xstr[pos] == '0':
xstr = xstr[:pos] + '1' + xstr[pos + 1:]
else:
xstr = xstr[:pos] + '0' + xstr[pos + 1:]
return int(xstr, 2)
3.3.3 总体代码
import random
# 交叉变异
def mutate(x, pos):
xstr = '{0:06b}'.format(x) # 转换为6位二进制
if xstr[pos] == '0':
xstr = xstr[:pos] + '1' + xstr[pos + 1:]
else:
xstr = xstr[:pos] + '0' + xstr[pos + 1:]
return int(xstr, 2)
# 繁衍,交换基因,x,y是数据,pos是从第几位开始交换
def exchange(x, y, pos):
xstr = '{0:06b}'.format(x) # 转换为6位二进制
ystr = '{0:06b}'.format(y) # 转换为6位二进制
tempxstr = '0b' + xstr[:pos] + ystr[pos:] # 临时存放
tempystr = '0b' + ystr[:pos] + xstr[pos:] # 临时存放
return int(tempxstr, 2), int(tempystr, 2) # 再转换为十进制
lt=[21,42,8,57]
#lt=[1,2,3,4]
for gen in range(0,10): #次数为代数
son1,son2=exchange(lt[0],lt[1],3) #1、2号繁衍2个后代,加入lt
lt.append(son1)
lt.append(son2)
son3,son4=exchange(lt[2],lt[3],3) #3、4号繁衍2个后代,加入lt
lt.append(son3)
lt.append(son4)
son5=mutate(lt[2],random.randint(0,5)) #根据第3个父数据变异
lt.append(son5)
son6=mutate(lt[3],random.randint(0,5)) #根据第4个父数据变异
lt.append(son6)
lt=sorted(lt,key=lambda x:x*x-19*x+20) #根据目标函数排序
print("第{}代的种群为{}".format(gen+1,lt))
ls=lt[:4]
lt=ls
x=lt[0]
print("最小的X是{},对应的y值为{}".format(x,x*x-19*x+20))
3.3.4 运行结果
第1代的种群为 [9, 8, 12, 21, 26, 37, 41, 42, 56, 57]
第2代的种群为 [9, 9, 8, 8, 8, 12, 5, 5, 21, 28]
第3代的种群为 [9, 9, 9, 9, 8, 8, 8, 8, 12, 24]
第4代的种群为 [9, 9, 9, 9, 9, 9, 9, 9, 13, 25]
第5代的种群为 [9, 9, 9, 9, 9, 9, 9, 9, 13, 25]
第6代的种群为 [9, 9, 9, 9, 9, 9, 9, 9, 13, 25]
第7代的种群为 [9, 9, 9, 9, 9, 9, 9, 9, 13, 25]
第8代的种群为 [9, 9, 9, 9, 9, 9, 9, 9, 13, 25]
第9代的种群为 [9, 9, 9, 9, 9, 9, 9, 9, 13, 25]
第10代的种群为 [9, 9, 9, 9, 9, 9, 9, 9, 13, 25]
最小的X是9,对应的y值为-70
3.4 思考与拓展
3.4.1 初始种群的规模与生成规则
初始种群:1,2,3,4
第1代的种群为[7, 4, 4, 3, 3, 2, 2, 1, 1, 20]
第2代的种群为[7, 7, 4, 4, 4, 4, 3, 3, 0, 19]
第3代的种群为[7, 7, 7, 7, 4, 4, 4, 4, 0, 20]
第4代的种群为[7, 7, 7, 7, 7, 7, 7, 7, 3, 23]
第5代的种群为[7, 7, 7, 7, 7, 7, 7, 7, 3, 23]
第6代的种群为[7, 7, 7, 7, 7, 7, 7, 7, 3, 23]
第7代的种群为[7, 7, 7, 7, 7, 7, 7, 7, 3, 23]
第8代的种群为[7, 7, 7, 7, 7, 7, 7, 7, 3, 23]
第9代的种群为[7, 7, 7, 7, 7, 7, 7, 7, 3, 23]
第10代的种群为[7, 7, 7, 7, 7, 7, 7, 7, 3, 23]
最小的X是7,对应的y值为-64
初始种群:
21
,
42
,
36
,
54
,
1
,
64
21,42,36,54,\color{red}{1,64}
21,42,36,54,1,64
第1代的种群为[9, 8, 12, 4, 15, 21, 26, 37, 41, 42, 52, 56, 57, 59, 63]
第2代的种群为[9, 9, 8, 8, 8, 12, 12, 5, 4, 15, 4, 17, 20, 21, 31]
第3代的种群为[9, 9, 9, 9, 8, 8, 8, 8, 8, 8, 8, 12, 12, 12, 24]
第4代的种群为[9, 9, 9, 9, 9, 9, 9, 9, 8, 8, 8, 8, 12, 13, 25]
第5代的种群为[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 13, 13, 25]
第6代的种群为[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 13, 13, 25]
第7代的种群为[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 13, 13, 25]
第8代的种群为[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 13, 13, 25]
第9代的种群为[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 13, 13, 25]
第10代的种群为[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 13, 13, 25]
最小的X是9,对应的y值为-70
3.4.2 遗传规则的设计:交叉、变异
采用随机数生成变异基因的位置
s
=
r
a
n
d
o
m
.
r
a
n
d
i
n
t
(
0
,
5
)
\color{red}{\mathbf{s=random.randint(0,5)}}
s=random.randint(0,5) #随机取0-5中任意数
#变异
def mutate(x):
s=random.randint(0,5) #随机取0-5中任意数
fb='{0:06b}'.format(x) #转换为6位二进制
if fb[pos]=='0':
sb=fb[:s] + '1' + fb[s+1:]
else:
sb=fb[:s] + '0' + fb[s+1:]
return int(sb,2)
4 课后延伸
- 启发式算法还包含:蚁群算法、模拟退火算法等,调研这些算法,并撰写报告;
- 请编写遗传算法部分的总结报告,包含:
(1)遗传算法的原理
(2)遗传算法的流程
(3)举一个计算实例说明其原理
(4)如何编写遗传算法的代码
(5)该算法的优缺点及如何改进