背景：

  最近我要学习二叉平衡树了，在学习二叉平衡树之前，我需要学会二叉搜索树，因为二叉平衡树就是根据二叉搜索树的思想进行优化的。

二叉查找树简介：

  二叉查找树是什么呢？（也叫二叉搜索树）就是字面意思，首先是一颗二叉树：一棵树，最多分两个叉。

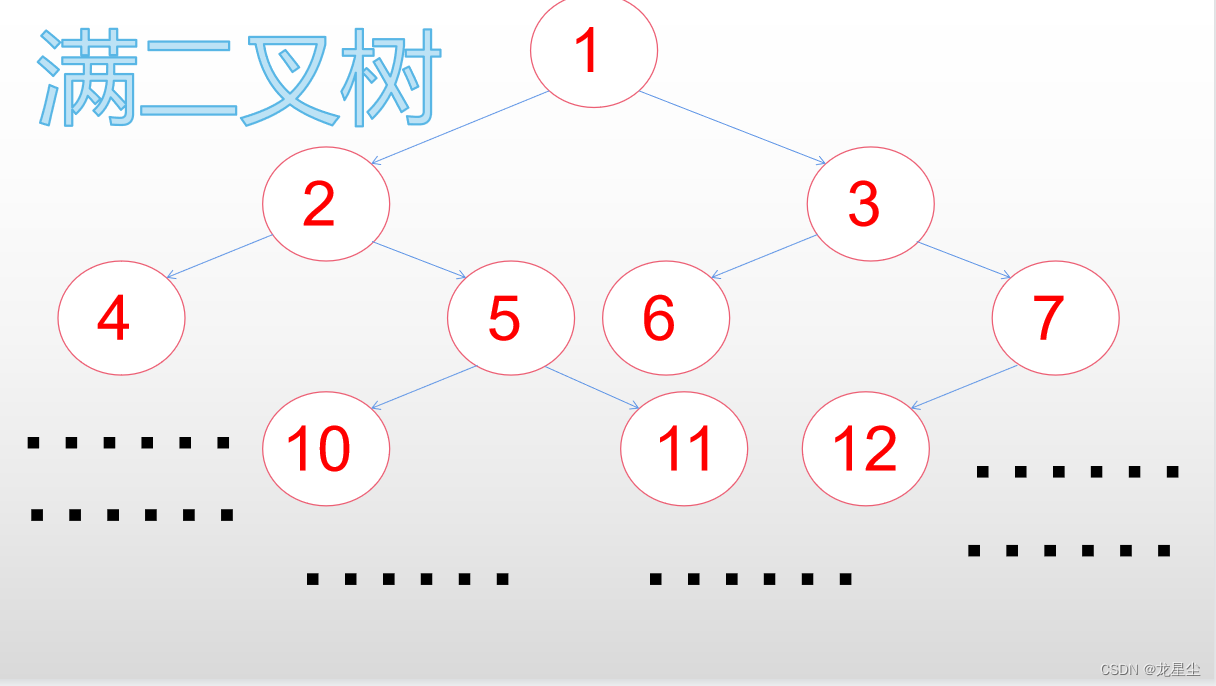
 上面那个图就是一颗二叉树，同时也是一颗满二叉树：每一个节点都有两个儿子，左儿子和右儿子。

  同时啊，还有完全二叉树：一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

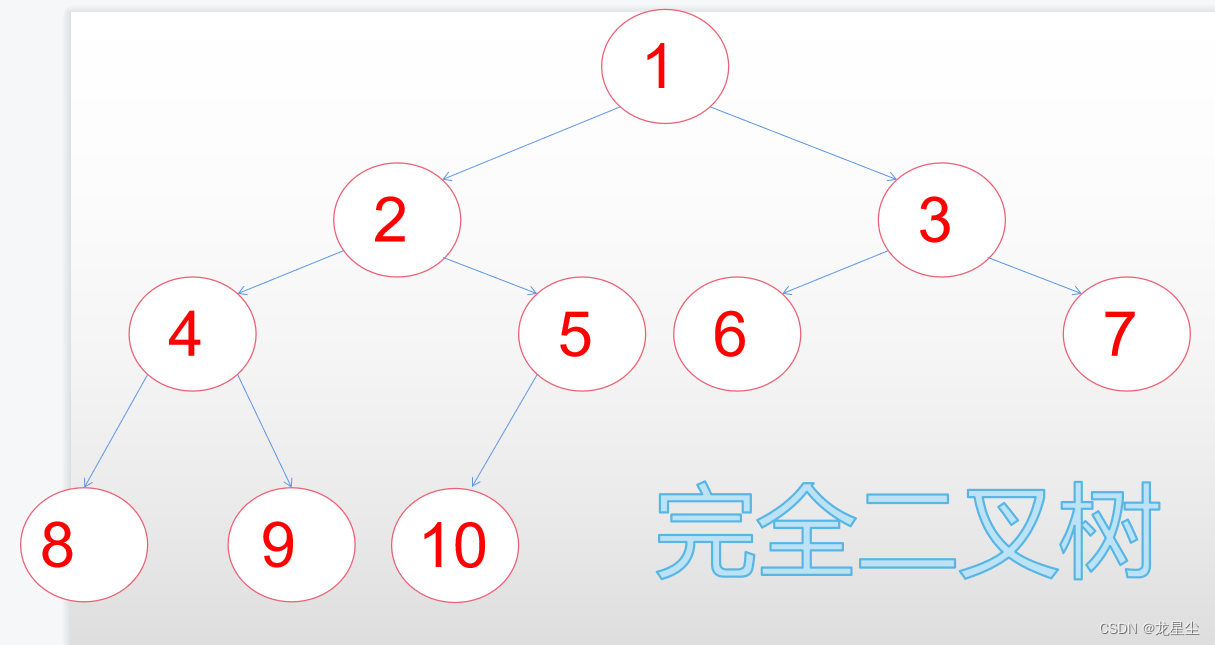
   然后最后一张图，就是普通的二叉树（就是只有每一个结点最多有两个儿子这一个特性）：

   然后，我们在看“搜索”，也就是说，我们建立起来的这颗二叉树，是用来搜索的，我们知道，搜索有很多种算法都可以，二分查找，枚举查找，启发式查找，为什么要用感觉很复杂的二叉树进行查找呢？那肯定是因为用二叉查找树来搜索比这些算法都快呀！

  接下来，给大家说一下二叉查找树的定义：一棵二叉树（满二叉树，完全二叉树，普通二叉树都可以），从根节点开始，根节点的左儿子一定小于根节点，根节点的右儿子肯定大于根节点，根节点的左儿子的左儿子也是一样，小于根节点的左儿子，根节点的左儿子的右儿子一定大于根节点的左儿子，以此类推，除了叶子节点，其他节点必须满足这个要求（等于的话算右儿子）

  也就是说，一棵二叉搜索树的所有左子节点肯定都小于根节点，所有的右子节点肯定都大于等于根节点，这样做有什么好处呢？首先，我们想要在二叉搜索树里查找一个数，首先比较第一个数与根节点的大小，如果一样，那就找到了，如果小于，那么前往左儿子那里继续重复这样的操作找，如果大于，那就前往右儿子那里继续重复这样的查找，直到找到为止。如果到了叶子节点，都没有找到这个数，那么在二叉搜索树里面就没有这个数。

  叶子结点就是一个没有左儿子和没有右儿子的结点（比方说上图1.3图中的4,8,9,6,10号结点就都是叶子结点）。

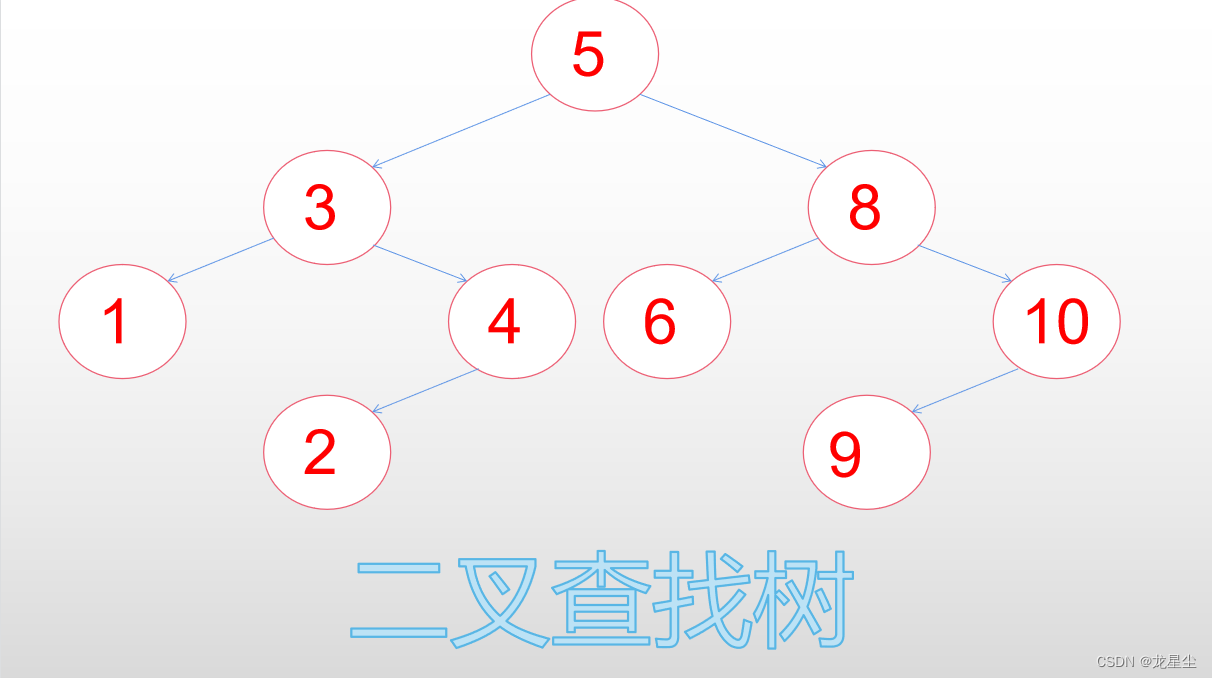
  以上这个图就是一棵二叉搜索树，每一个结点都符合左儿子小于结点，右儿子大于结点这一个条件，看上面这个数，是我们输入9个数之后建成的，如果用数组进行查找的话，最快需要1次，最久需要9次才可以找到，而这个二叉搜索树最快是1次，最慢只要3次就可以了，是按树的高度来计量的（而二分查找虽说有些时候是比二叉搜索树快，但是必须满足数组有序才可以，对于输入数据无序的情况来说，还是二叉搜索树好一些）。

  所以说，二叉搜索树搜索一个数的时间复杂度为O(logh)(h为二叉搜索树的高度,h最大为n,h最小为x,n为输入数的数量,2^x>=n).

程序（字典序）：

  介绍：

    就是输入n个字符串，以字典序来进行创建二叉搜索树，字典序就是A~Z(保证输入字符串第一个字符为大写),首先比较第一个字符，比较二者的ASCII码，如果相等就比较下一个字符。

  结构体：

    首先，我们需要定义一个二叉树的结构Node，每一个结点里面存着一个字符串，可以定义一个char*类型的数组a,初始化为'\0'.

  然后是两个bool类型的变量lf和rf,初始化为false,代表着这个节点是否有左儿子，是否有右儿子，然后就是定义两个结构指针Node* lchidl和Node* rchild.分别表示左儿子和右儿子，都初始化为NULL（为空）。

struct Node{ //节点结构 
	char a[101]; //节点中的字符串 
	Node *lchild; //节点的左儿子 
	bool lf; //是否有左儿子 
	Node *rchild; //节点的右儿子 
	bool rf; //是否有右儿子 
	Node(){ //初始化 
		lchild=rchild=NULL; //左儿子和右儿子初始化为NULL(空) 
		lf=rf=false; //bool类型的rf和lf先初始化为false(假) 
	}
};

  初始化函数：

    因为我们在结构体里面定义的初始化函数只有根节才可以使用，初始化rchild和lchild的时候，我们需要用特定的一个初始化函数init来进行。

void init(Node* q){ //初始化函数init 
	q->lchild=q->rchild=NULL; //将左儿子和右儿子设置为NULL(空) 
	q->lf=q->rf=false; //将是否有左儿子、右儿子设置为false(假) 
	for(int i=0;i<101;i++) //进行初始化字符串 
	  q->a[i]='\0'; //将其设置为\0(空字符) 
}

   比较函数：

  我们需要写一个bool返回值的比较函数cmp，参数为两个字符串，是判断在字典序中，谁大谁小的。

bool cmp(char a[101],char b[101]){ //判断字符串谁大谁小 
	int t=strlen(a),t1=strlen(b); //求两个长度 
	if(t<t1){ //如果a长 
		for(int i=0;i<t;i++){ //比较 
			if(a[i]<b[i]) //ASCII码比较小的话 
			  return false; //返回false 
			if(a[i]>b[i]) //ASCII码比较大的话 
			  return true; //返回true 
		}
		return false; //如果执行完了,都没有返回，说明b是a的一个连续子串,返回false. 
	}
	else if(t1<t){
		for(int i=0;i<t1;i++){ //比较 
			if(a[i]<b[i]) //ASCII码比较小的话 
			  return false; //返回false 
			if(a[i]>b[i]) //ASCII码比较大的话 
			  return true; //返回true 
		}
		return false; //如果执行完了,都没有返回，说明a是b的一个连续子串,返回false.
	}
	for(int i=0;i<t1;i++){ //如果长度相同 
		if(a[i]<b[i]) //ASCII码比较小的话 
		  return false; //返回false 
		if(a[i]>b[i]) //ASCII码比较大的话 
		  return true; //返回true 
	}
}

  插入字符串

  接下来我们要写一个插入字符串的insert函数，参数为Node* q,char s[101]，代表在q这个二叉查找树中插入s这个字符串。

  我们可以从根节点开始比较，如果小就去左儿子节点，如果大就去右儿子节点，如果到了一个节点，左子节点和右子节点都为NULL（空），那么就可以将s插入在这个位置。

bool insert(Node* q,char s[101]){ //插入s字符串到q上 
	while(1){ //一直执行 
		if(q->rchild==NULL&&q->lchild==NULL&&q->a[0]=='\0'){ //如果这个节点没有左子节点和右子节点,并且节点字符串为空 
			for(int i=0;i<strlen(s);i++) //进行插入操作 
			  q->a[i]=s[i]; //赋值 
			return true; //返回插入成功 
		}
		bool f=cmp(q->a,s); //比较当前节点字符串和s的大小 
		if(f){ //如果为真(小),去左子节点 
			if(!q->lf){ //如果这个节点没有左子节点 
				q->lchild=(Node*)malloc(sizeof(Node)); //分配空间 
				q->lf=true; //初始化 
				init(q->lchild); //初始化函数 
			}
			q=q->lchild; //前往 
		}
		else{ //如果为假(大) 
			if(!q->rf){ //如果这个节点没有右子节点
				q->rchild=(Node*)malloc(sizeof(Node));//分配空间 
				q->rf=true; //初始化 
				init(q->rchild); //初始化函数 
			}
			q=q->rchild; //前往 
		}
	}
	return false; //返回假 
}

判断函数

  函数pd的作用是比较两个字符串是否相等（在查找的时候需要用）！

bool pd(char a[101],char b[101]){ //判断a字符串和b字符串是否相等 
	if(strlen(a)!=strlen(b)) //如果长度都不一样 
	  return false; //肯定不一样 
	for(int i=0;i<strlen(a);i++) //每一个字符逐一对比 
	  if(a[i]!=b[i]) //如果有一个不一样的 
	    return false; //返回假 
	return true; //返回真 
}

查找函数

  我们还需要写一个查找函数searc，参数为Node* q,char s[101].是在q这个二叉搜索树中找s这个字符。

  我们可以应用递归的形式,如果q->lf为真，递归去q->lchild看看，如果q->rf为真，递归去q->rchild看看，每次到一个节点，都要比较这个结点和s是不是一样（pd函数），如果一样，返回为真。

void search(Node *q,char s[101]){ //在q里面查找s字符串 
	if(cz) //如果为真 
	  return ; //返回 
	sum++; //次数累计 
	if(pd(q->a,s)){ //如果相等 
		cz=true; //赋值为真 
		return ; //退出 
	}
	if(q->lf) //如果有左子节点 
	  if(cmp(q->a,s)) //比较 
	    search(q->lchild,s); //递归 
	if(q->rf) //如果有右子节点 
	  if(!cmp(q->a,s)) //比较 
	    search(q->rchild,s); //递归 
	return ; //返回 
}

输出二叉搜索树：

  我们可以写一个输出函数print，就是用来输出一颗二叉搜索树，也是和查找一样，运用递归的方式。

void print(Node* q){ //输出二叉搜索树 
	cout<<q->a<<endl; //输出这个节点的字符串 
	if(q->lchild==NULL&&q->rchild==NULL) //如果是叶子节点 
	  return ; //返回 
	if(q->lf) //如果有左子节点 
	  print(q->lchild); //递归 
	if(q->rf) //如果有右子节点 
	  print(q->rchild); //递归 
}

main主函数：

int main(){
	int n;
	cin>>n;
	char a[n][101];
	Node* p;
	p=(Node*)malloc(sizeof(Node));
	cin>>a[0];
	for(int i=0;i<strlen(a[0]);i++)
	  p->a[i]=a[0][i];
	for(int i=1;i<n;i++){
		cin>>a[i];
		bool f=insert(p,a[i]);
		if(!f){
			cout<<"插入失败!\n";
			return 0;
		}
	}
	cout<<endl; 
	print(p);
	char s[101];
	cout<<"输入要查找的字符串:\n";
	cin>>s;
	search(p,s);
	if(cz)
	  printf("查找成功,查找次数为%d!\n",sum);
	else
	  printf("二叉查找树中没有这个字符串!\n");
	return 0;
}

完整代码： 

#include<bits/stdc++.h>
using namespace std;
int sum=0;
bool cz;
struct Node{ //节点结构 
	char a[101]; //节点中的字符串 
	Node *lchild; //节点的左儿子 
	bool lf; //是否有左儿子 
	Node *rchild; //节点的右儿子 
	bool rf; //是否有右儿子 
	Node(){ //初始化 
		lchild=rchild=NULL; //左儿子和右儿子初始化为NULL(空) 
		lf=rf=false; //bool类型的rf和lf先初始化为false(假) 
	}
};
bool cmp(char a[101],char b[101]){ //判断字符串谁大谁小 
	int t=strlen(a),t1=strlen(b); //求两个长度 
	if(t<t1){ //如果a长 
		for(int i=0;i<t;i++){ //比较 
			if(a[i]<b[i]) //ASCII码比较小的话 
			  return false; //返回false 
			if(a[i]>b[i]) //ASCII码比较大的话 
			  return true; //返回true 
		}
		return false; //如果执行完了,都没有返回，说明b是a的一个连续子串,返回false. 
	}
	else if(t1<t){
		for(int i=0;i<t1;i++){ //比较 
			if(a[i]<b[i]) //ASCII码比较小的话 
			  return false; //返回false 
			if(a[i]>b[i]) //ASCII码比较大的话 
			  return true; //返回true 
		}
		return false; //如果执行完了,都没有返回，说明a是b的一个连续子串,返回false.
	}
	for(int i=0;i<t1;i++){ //如果长度相同 
		if(a[i]<b[i]) //ASCII码比较小的话 
		  return false; //返回false 
		if(a[i]>b[i]) //ASCII码比较大的话 
		  return true; //返回true 
	}
}
bool pd(char a[101],char b[101]){ //判断a字符串和b字符串是否相等 
	if(strlen(a)!=strlen(b)) //如果长度都不一样 
	  return false; //肯定不一样 
	for(int i=0;i<strlen(a);i++) //每一个字符逐一对比 
	  if(a[i]!=b[i]) //如果有一个不一样的 
	    return false; //返回假 
	return true; //返回真 
}
void init(Node* q){ //初始化函数init 
	q->lchild=q->rchild=NULL; //将左儿子和右儿子设置为NULL(空) 
	q->lf=q->rf=false; //将是否有左儿子、右儿子设置为false(假) 
	for(int i=0;i<101;i++) //进行初始化字符串 
	  q->a[i]='\0'; //将其设置为\0(空字符) 
}
bool insert(Node* q,char s[101]){ //插入s字符串到q上 
	while(1){ //一直执行 
		if(q->rchild==NULL&&q->lchild==NULL&&q->a[0]=='\0'){ //如果这个节点没有左子节点和右子节点,并且节点字符串为空 
			for(int i=0;i<strlen(s);i++) //进行插入操作 
			  q->a[i]=s[i]; //赋值 
			return true; //返回插入成功 
		}
		bool f=cmp(q->a,s); //比较当前节点字符串和s的大小 
		if(f){ //如果为真(小),去左子节点 
			if(!q->lf){ //如果这个节点没有左子节点 
				q->lchild=(Node*)malloc(sizeof(Node)); //分配空间 
				q->lf=true; //初始化 
				init(q->lchild); //初始化函数 
			}
			q=q->lchild; //前往 
		}
		else{ //如果为假(大) 
			if(!q->rf){ //如果这个节点没有右子节点
				q->rchild=(Node*)malloc(sizeof(Node));//分配空间 
				q->rf=true; //初始化 
				init(q->rchild); //初始化函数 
			}
			q=q->rchild; //前往 
		}
	}
	return false; //返回假 
}
void print(Node* q){ //输出二叉搜索树 
	cout<<q->a<<endl; //输出这个节点的字符串 
	if(q->lchild==NULL&&q->rchild==NULL) //如果是叶子节点 
	  return ; //返回 
	if(q->lf) //如果有左子节点 
	  print(q->lchild); //递归 
	if(q->rf) //如果有右子节点 
	  print(q->rchild); //递归 
}
void search(Node *q,char s[101]){ //在q里面查找s字符串 
	if(cz) //如果为真 
	  return ; //返回 
	sum++; //次数累计 
	if(pd(q->a,s)){ //如果相等 
		cz=true; //赋值为真 
		return ; //退出 
	}
	if(q->lf) //如果有左子节点 
	  if(cmp(q->a,s)) //比较 
	    search(q->lchild,s); //递归 
	if(q->rf) //如果有右子节点 
	  if(!cmp(q->a,s)) //比较 
	    search(q->rchild,s); //递归 
	return ; //返回 
}
int main(){
	int n;
	cin>>n;
	char a[n][101];
	Node* p;
	p=(Node*)malloc(sizeof(Node));
	cin>>a[0];
	for(int i=0;i<strlen(a[0]);i++)
	  p->a[i]=a[0][i];
	for(int i=1;i<n;i++){
		cin>>a[i];
		bool f=insert(p,a[i]);
		if(!f){
			cout<<"插入失败!\n";
			return 0;
		}
	}
	cout<<endl; 
	print(p);
	char s[101];
	cout<<"输入要查找的字符串:\n";
	cin>>s;
	search(p,s);
	if(cz)
	  printf("查找成功,查找次数为%d!\n",sum);
	else
	  printf("二叉查找树中没有这个字符串!\n");
	return 0;
}
/*
12
Jan
Feb
Mar
Apr
May
Jun
Jul
Aug
Sep
Oct
Nov
Dec
*/

 运行样例:

输入：

12
Jan
Feb
Mar
Apr
May
Jun
Jul
Aug
Sep
Oct
Nov
Dec

 输出：

Jan
Feb
Apr
Aug
Dec
Mar
Jun
Jul
May
Sep
Oct
Nov
输入要查找的字符串:
Oct
查找成功,查找次数为11!

总结;

  二叉搜索树是一个搜索速度很快的数据结构，但是他还有一种很严重的缺点，需要用二叉平衡树来进行优化。