文章目录

C++011-C++循环+枚举
- 枚举
- - 枚举思想
  - 枚举举例
  - 题目描述统计因数
  - 题目描述质数判定
  - - 错误方法一：
    - 优化方法1：用break实现优化
    - 优化方法2： sqrt(n)
  - 题目描述水仙花数
  - 题目描述 7744问题
  - - 实现方法1
    - 优化方法2
  - 题目描述余数相同问题
  - 题目描述特殊自然数
  - 总结
  - 作业
- 在线练习：
- 总结

C++011-C++循环+枚举

在这里插入图片描述

在线练习：
http://noi.openjudge.cn/
https://www.luogu.com.cn/

枚举

在数学和计算机科学理论中，一个集的枚举是列出某些有穷序列集的所有成员的程序，或者是一种特定类型对象的计数。这两种类型经常（但不总是）重叠。枚举是一个被命名的整型常数的集合！。

在这里插入图片描述

枚举思想

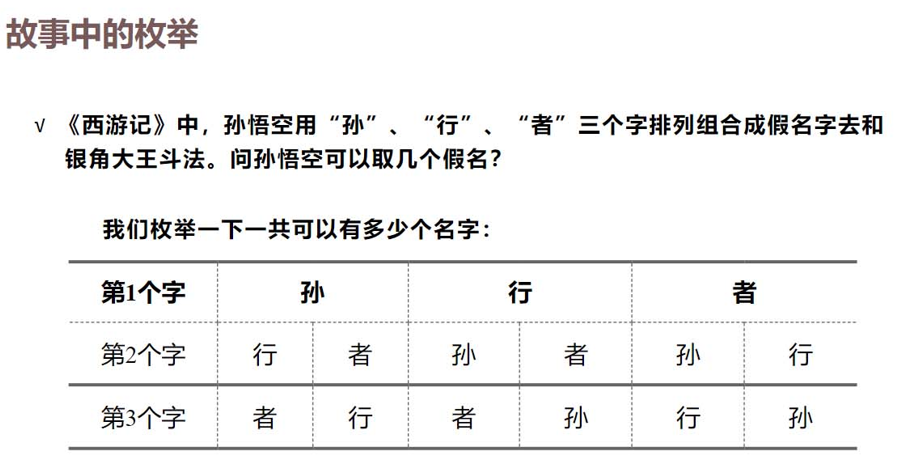
枚举:列出某些有穷序列集的所有成员，或者对一种特定类型对象的计数

①有限的范围
②所有的成员
③特定的类型

根据枚举的定义：
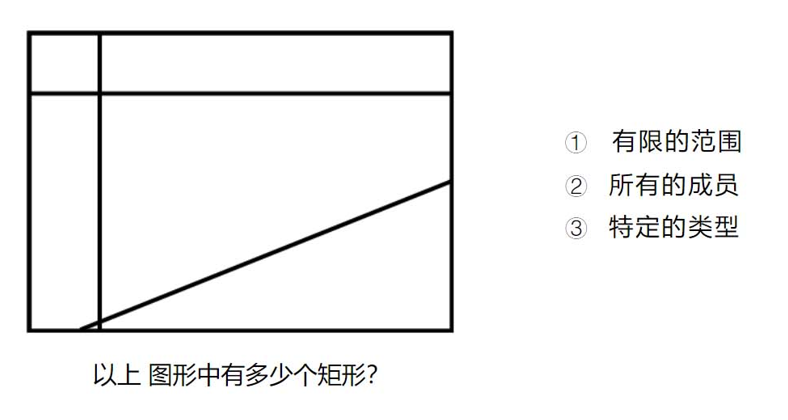
在这里插入图片描述

数图形的时候∶

只在一个大图中数。——有限的范围
要求在各种几何形状数图形——所有的成员
从中统计矩形的数量——特定的类型

有同学可能会问∶所有的成员为什么是各种几何图形，而不是所有的矩形呢?
归根结底就是枚举时宁可多，但不能漏!

如果能确定某个问题的答案在一定的范围内，那么我们就列举这个范围内的所有成员（或者确定能包括答案的特定成员)，再通过筛选和判断锁定特定类型，最后得出答案。

定范围
列成员
选类型
算答案

枚举举例

题目描述统计因数

题目描述
任意一个自然数N都可以分解质因数，如果写出如下形式：
$N=P_{1}^{M1}*P_{2}^{M2}*...*P_{n}^{Mn}$
那么N一共有有 $(M 1 + 1) * (M 2 + 1) * ... * (M n + 1)$ 个因数，包括1和N本身
例如 $36=2^{2}*3^{2}$ ，那么36一共有(2+1)*(2+1)=9个因数，包括1和36.
解题思路
用枚举思想来验证：

定范围：36的因数一定是1到36之间的正整数
列成员 1 2 3 4 …36
选类型+算答案 1.2.3.4.6.9.12.18.36，共9个。

#include <iostream>
//#include<bits/stdc++.h>

using namespace std;

int main()
{
    int s=0;
    for(int i =1; i<=36; i++ )
    {
        if(36%i==0) {
                cout<<i<<" ";
                s++;
        }
    }
    cout<<endl<<s;

    return 0;
}

输出为：
在这里插入图片描述

题目描述质数判定

题目描述
如果一个数n，除了1和他本身，没有其他的因数，这个数就是质数
方法一：枚举所有可能是n的因数的数，统计有多少个因数，如果只有两个，那么这个数是质数，否则不是。
方法二：枚举2到n-1之间的自然数，如果存在n的因数，那么这个数可定不是质数，如果不存在n的因数，那么这个数是质数

那么我们怎么“定范围”?——按照方法一的话，范围就是1到这个数本身。
怎么列成员——列举所有的自然数
怎么选类型——判断是否能整除给定数字
怎么算答案——找到一个整除的，则统计因数增加一次，最后看有多少个因数。如果只有2个，那就是质数，否则是合数。

错误方法一：

#include <iostream>
//#include<bits/stdc++.h>

using namespace std;

int main()
{
    int n=0;
    cin>>n;
    int flag = 1;//1表示是质数，0表示不是质数
    for(int i =2; i<=n-1; i++ )
    {
        if(n%i==0) {
                flag = 0;
        }
        else{
            flag = 1;
        }
    }
    if(flag==1) cout<<"是质数";
    else cout<<"不是质数";

    return 0;
}

优化方法1：用break实现优化

#include <iostream>
//#include<bits/stdc++.h>

using namespace std;

int main()
{
    int n=0;
    cin>>n;
    int flag = 1;//1表示是质数，0表示不是质数
    for(int i =2; i<=n-1; i++ )
    {
        if(n%i==0) {
                flag = 0;
                break;
        }
    }
    if(flag==1) cout<<"是质数";
    else cout<<"不是质数";

    return 0;
}

质数判定的进一步优化∶平方根优化。其实我们还可以进一步缩小枚举的范围。过去我们枚举的范围是2到n-1，其实并不必要，只要枚举2-sqrt(n)即可。这是因为，如果n能够分解成两个数的乘积，那么其中一个必须≤sqrt(n)，另外一个≥sqrt(n);这里，sqrt(n)表示n的平方根。
_{测试2147483647}

优化方法2： sqrt(n)

#include <iostream>
#include<cmath>
//#include<bits/stdc++.h>

using namespace std;

int main()
{
    int n=0;
    cin>>n;
    int flag = 1;//1表示是质数，0表示不是质数
    int t = sqrt(n);
    for(int i =2; i<=t; i++ )
    {
        if(n%i==0) {
                flag = 0;
                break;
        }
    }
    if(flag==1) cout<<"是质数";
    else cout<<"不是质数";

    return 0;
}

题目描述水仙花数

题目描述
水仙花数是一种自幂数，有如下两个特点：
1.是三位数
2.各个数位上的数字的三次方和等于他本身，六日
153= 111 + 555 + 333
输入
无
输出
所有的水仙花数，每一个数字占一行。
样例输入
无
样例输出
153
…
解题思路

定范围：所有的三位数 100-999
列成员：100-999之间所有的自然数
选类型：符合各个数位上数字的三次方和等于本身的才是特点的类型
算答案：找到特点类型数字马上输出

#include <iostream>
//#include<bits/stdc++.h>

using namespace std;

int main()
{

    for(int i =100; i<=999; i++ )
    {
        int a=i/100,b=i/10%10,c=i%10;
        if(a*a*a+b*b*b+c*c*c==i) cout<<i<<endl;

    }
    return 0;
}

输出入下：
在这里插入图片描述

题目描述 7744问题

题目描述
列出所有满足下列条件的数字
1.是四位数
2.是完全平方数
3.前2位数字相同，后2位数字也相同
输入
无
输出
每行一个符合条件的数字
样例输入
无
样例输出
7744
…

实现方法1

定范围：所有的四位数 1000-9999
列成员：100-9999之间所有的自然数
选类型：
符合完全平方数，即sqrt(i) = (int)sqrt(i);
且前2位数字相同，后两位数字相同
int a = i/1000,b=i/100%10,c=i/10%10,d=i%10;
if(a==b && c==d)
算答案：找到特点类型数字马上输出

#include <iostream>
#include<cmath>
//#include<bits/stdc++.h>

using namespace std;

int main()
{

    for(int i =1000; i<=9999; i++ )
    {
        if(sqrt(i)==(int)sqrt(i))
        {
            int a=i/1000,b=i/100%10,c=i/10%10,d=i%10;
            if(a==b&&c==d) cout<<i<<endl;

        }

    }
    return 0;
}

优化方法2

【7744问题-浮点数运算有误差，如果想避开浮点数应该如何做?】

列成员
用循环变量直接列举1000~9999的完全平方数;
枚举i*i的值，而不是仅枚举i，我们需要根据此需要确定i的范围
定范围
由10000>9999> =i*i>=1000推知:99> =i>=32 ;
for(int i=32;i<=99;i++){
int t=i*i;
}
选类型
前两位相同，后两位相同
把四个数位上数字分别取出再比较:
int a=t/1000,b=t/100%10,c=t/10%10,d =t%10;. if(a= =b&&c==d)则前两位相同，后两位相同;
算答案:
符合条件的t是答案

#include <iostream>
//#include<bits/stdc++.h>

using namespace std;

int main()
{

    for(int i =32; i<=99; i++ )
    {
        int t=i*i;
        int a=t/1000,b=t/100%10,c=t/10%10,d=t%10;
        if(a==b&&c==d) cout<<t<<endl;
    }
    return 0;
}

题目描述余数相同问题

题目描述
已知三个正整数a,b,c。
现有一个大于1的整数x，将其作为除数分别除a, b，c，得到的余数相同。请问满足上述条件的x的最小值是多少?
数据保证x有解。
输入
一行，三个不大于1000000的正整数a， b，c，两个整数之间用一个空格隔开。
输出
一个整数，即满足条件的x的最小值。
样例输入
300 262 205
样例输出
19
…

定范围：
数据保证有解，只需要求x最小的值。上限不需确定，找到解后，break就可。
保险起见，余数不会大于被除数和除数，范围可以设定位2到三个数字中的任意一个。
列成员：
从小到大列举范围内的整数
for(int i=2;i<=a;i++){
}
选类型：
分别除以a,b,c 得到的余数相同 a%i==b%i&&b%i==c%i
算答案：
找到特点类型数字i马上输出

#include <iostream>
//#include<bits/stdc++.h>

using namespace std;

int main()
{
    int a,b,c;
    cin>>a>>b>>c;
    for(int i=2;i<=a;i++){
        if(a%i==b%i && b%i==c%i){
            cout<<i;
            break;
        }
    }
    return 0;
}

题目描述特殊自然数

题目描述
一个十进制自然数，他的七进制和九进制表示都是三位数，且七进制和九进制数码的表示顺序正好相反，编程求此自然数，并输出显示。
输入
无
输出
三行：
第一行是此自然数的十进制表示；
第二行是此自然数的七进制表示；
第三行是此自然数的九进制表示。
样例输入
无
样例输出
略
…

预备知识

十进制与N进制的互相转换：
N进制：位权为N的数制。
十进制： $1234)_{10}=1*10^{3}+2*10^{2}+3*10^{1}+4*10^{0}$
从低位到高位分别为第0位，第1位，第2位…
七进制：
$1234)_{7}=1*7^{3}+2*7^{2}+3*7^{1}+4*7^{0}$
把N进制的数字按照位权展开，计算得到的数字就是十进制的数字了。
N进制下的数位拆分：
十进制下，M%10=十进制表示下的最末尾。
N进制下，M%N=N进制表示下的最末尾。
$1234)_{7}=1*7^{3}+2*7^{2}+3*7^{1}+4*7^{0}$
$1234)_{7}\%7=(1*7^{3}+2*7^{2}+3*7^{1}+4*7^{0})\%7=4$ 余数定理

在这里插入图片描述

定范围：
在十进制下定范围，七进制和九进制下是三位数
七进制下的最大数位666，最小的三位数位100，转换为十进制得到范围为 $100)_{7}=49,(666)_{7}=6*49+6*7+6*1=342$ 范围i为[49,342]
九进制下的最大数位888，最小的三位数位100，转换为十进制得到范围为 $100)_{9}=81,(888)_{9}=8*81+8*9+8*1=728$ 范围i为[81,728]
取公共部分，这个数在十进制表示下，应属于[81,342]
列成员：
列举从81-342范围内的整数
for(int i=81;i<=342;i++){
}
选类型：
七进制和九进制下数字正好相反，设七进制下ABC，九进制下abc
int A=i/7/7%7,B=i/7%7,C=i%7;
int a=i/9/9%9,b=i/9%9,C=i%9;
如果A==c&&B==b&&C==c，那么i符合题意
算答案：
若符合提议，则输出答案，依次输出i,ABC,abc每个答案占据一行

#include <iostream>
//#include<bits/stdc++.h>

using namespace std;

int main()
{
    for(int i=81;i<=342;i++){
        int A,B,C,a,b,c;
        A=i/7/7%7,B=i/7%7,C=i%7;
	    a=i/9/9%9,b=i/9%9,c=i%9;
        if(A==c&&B==b&&C==a){
            cout<<i<<endl;
            cout<<A<<B<<C<<endl;
            cout<<a<<b<<c<<endl;
        }
    }
    return 0;
}