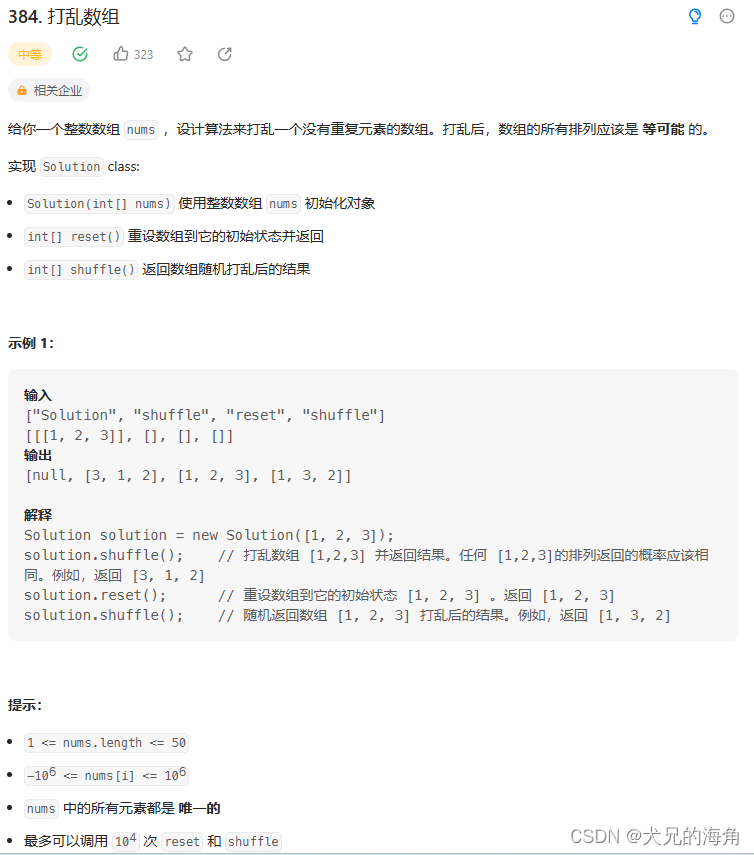
1、列表随机

为了能够初始化数组，我们使用nums保存当前的数组，利用orignal保存初始化数组。为了实现等可能随机打乱，考虑到随机数本质上是基于随机数种子的伪随机，我们采用如下的方式实现等可能随机：我们将所有元素压入列表，每次随机选择一个位置上的数字，按顺序将其放入打乱后的数组中，而后我们从列表中删除当前元素。

class Solution {
private:
    vector<int> nums;
    vector<int> orignal;
public:
    Solution(vector<int> &nums) {
        this->orignal = nums;
        this->nums = nums;
    }

    vector<int> reset() {
        this->nums = this->orignal;
        return this->nums;
    }

    vector<int> shuffle() {
        vector<int> shuffled(nums.size());
        list<int> lst(nums.begin(), nums.end());
        for (int i = 0; i < nums.size(); ++i) {
            int j = rand() % (lst.size());
            auto it = lst.begin();
            advance(it, j);
            shuffled[i] = *it;
            lst.erase(it);
        }
        copy(shuffled.begin(), shuffled.end(), nums.begin());
        return nums;
    }
};

2、Fisher-Yates 洗牌算法

考虑到方法一中随机打乱的时间复杂度达到$O(n^2)$，我们可以对随机打乱的方式进行进一步的改进：我们在第i次循环中，在$[i,n)$中随机选择一个位置j上的元素将其与位置i上的元素进行交换，如此循环直至n次。这样做能够确保我们在$O(n)$的时间复杂度内实现随机打乱。

class Solution {
private:
    vector<int> nums;
    vector<int> orignal;
public:
    Solution(vector<int> &nums) {
        this->orignal = nums;
        this->nums = nums;
    }

    vector<int> reset() {
        return this->orignal;
    }

    vector<int> shuffle() {
        for (int i = 0; i < nums.size(); ++i) {
            int j = i + rand() % (nums.size() - i);
            swap(nums[i], nums[j]);
        }
        return nums;
    }
};