前言

This week,the paper proposes a Multi-directional Temporal Convolutional Artificial Neural Network (MTCAN) model to impute and forecast PM2.5 pollutant concentration in a single training process.The main idea of the multi-directional properties of MTCAN is to interpolate the PM2.5 pollutant feature matrix to impute its value. In addition, the relevant knowledge of cellular automata is learned.

本周阅读文献《Multi-directional temporal convolutional artificial neural network for PM2.5 forecasting with missing values: A deep learning approach 》，文献主要提出了多向时间卷积人工神经网络模型（MTCAN）用来预测PM2.5的污染物浓度，MTCAN多向特性的主要思想是插入PM2.5污染物特征矩阵以估算其值，实验表明所提模型的有效性。另外学习了元胞自动机的相关知识。

文献阅读

题目：Multi-directional temporal convolutional artificial neural network for PM2.5 forecasting with missing values: A deep learning approach
作者：K. Krishna Rani Samal , Korra Sathya Babu , Santos Kumar Das

摘要

数据插补和预测是环境数据工程的主要研究领域。缺失数据是所有领域的常见问题，尤其是对于环境数据分析。大多数研究都试图使用不同的模型解决时间序列数据的问题。本研究提出了一种基于深度学习的混合模型架构多向时间卷积人工神经网络（MTCAN）模型，在单个训练过程中估算和预测PM2.5污染物浓度。MTCAN多向特性的主要思想是插入PM2.5污染物特征矩阵以估算其值。最终，它保持要素测量值与气象和污染物变量内的时间相关性，以插补PM2.5缺失值。实验结果表明，所提模型优于基线污染预测模型，证明了其在空气质量建模中的有效性。

主要贡献

开发了有效的多方向插补技术，利用不同时间戳下污染物和气象因素的不同参数之间的相关性，并考虑每个参数的其他测量值之间的相关性。最终，它利用每个参数测量值之间的相关性，及每个特征之间的相关性来估算PM2.5缺失值。
MTCAN模型并行集成了卷积神经网络（CNN）的快速特征提取能力和循环神经网络（RNN）的顺序时间建模特征，提高了预测精度。采用残差映射的扩张卷积方法考虑大量过去数据，不会有从未来到过去的信息丢失。
通过使用微调层，预测准确性进一步增强。该层根据预测值和观测值相关性调整先前训练的预测模型的神经元权重。

数据插补技术
具有不一致缺失数据的空气质量建模是环境建模的主要问题之一。一种方法是使用部分可用的其他参数值插补缺失值，第二种方法是通过插补预测值恢复缺失的属性。插值技术通常使用部分存在的参数值的平均值、中位数和众数来预测缺失值;当每个参数值都很重要时，这些技术很重要。这些技术尝试通过仅捕获数据流中的时间相关性来重建数据，但忽略其他流的相关性。相比之下，插补技术捕获数据流的时间相关性，但忽略数据流中测量值的时间相关性。插补技术分为两种类型，即简单的插补技术，例如均值、中位数和模数插补技术。第二种插补技术是多重插补技术，如最大似然、期望最大化（EM）和基于KNN的插补。

方法框架

本文提出的多向时序卷积神经网络（MTCAN）模型的多向属性同时包括插值块和插补块，它在前向和后向都进行了操作。MTCAN模型考虑气象因子与PM10污染物之间的相关性，以提高PM2.5的数据质量和长期预测性能。MTCAN模型包括用于时间序列预测的TCN模型和用于微调预测结果的ANN模型。

用于时间序列预测的时间卷积人工神经网络
CNN的扩展版本时间卷积网络TCN，与RNN相比，CNN通常仅用于特征提取目的，而不是用于顺序建模，因为缺乏处理长序列的存储块。然而，作为CNN的一种变体，TCN在训练效率方面优于RNN结构。该模型的主要组成部分是一维卷积、因果卷积、扩张卷积和残差块。TCN的卷积可以捕获局部信息，因此在时间建模方面效果更好。扩张因果卷积的感受野使我们能够捕获更多的输入特征。它可以并行执行特征学习和预测，以提高预测性能。与RNN不同，它可以接受任何长度的输入并将其映射到输出序列的相同长度。TCN使用全连接神经网络（FCNN）来实现这一目标。TCN具有卷积，本质上是因果关系，因此它可以确保没有信息从未来泄漏到过去。它生成顺序预测结果。

因果卷积基本设计的主要缺点是它需要深度网络或较大的过滤器大小才能获得较长的有效历史大小，这不支持基本结构。较大的过滤器尺寸会导致非收敛问题，而较大的更深的网络会导致训练问题，最终降低模型预测性能。为了解决这些限制，在TCN结构中采用了扩张因果卷积，其中膨胀因子随着网络深度的增加而增加。它具有扩展感受野的能力。因此，TCN通过使用更大的感受野和不使用更大的滤波器尺寸来实现更好的计算效率。

扩张因果卷积
元素 e 的输入序列 x 的卷积操作可以定义为
在这里插入图片描述元素 e 的膨胀卷积操作可以定义为
其中 f（m）是 m千其对应层的滤波器数，d为膨胀因子，k表示滤波器尺寸，e−d。m是过去的方向。当 d 变为 1 时，膨胀的因果卷积成为标准的因果卷积。较大的膨胀系数允许输出端的神经元表示广泛的输入历史数据，并且还提供了扩展更大感受野的灵活性。

扩张因果卷积的图形示意图如图：
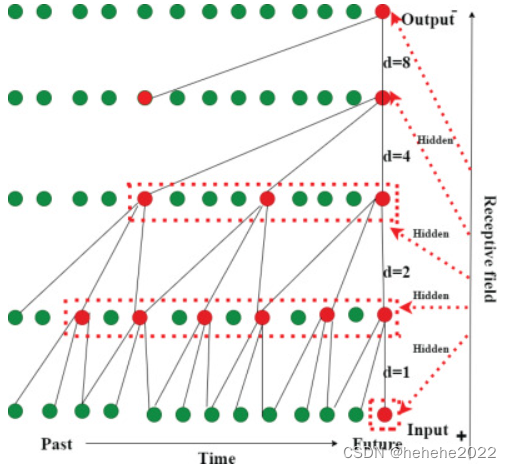在这里插入图片描述残差映射
残差映射函数可以表述为

其中φ是非线性激活函数。

在所提出的架构中，TCN在残差块内具有两层膨胀的因果卷积和非线性。泄漏ReLU用作非线性激活函数。对卷积滤波器采用权重归一化过程进行归一化。此外，残差块还具有最大池化层和辍学层。采用最大池化操作来减小数据大小和计算复杂度。在每次扩张因果卷积后添加损失为 0.1 的 dropout 层，以避免训练模型时出现过拟合问题。

实验

实验数据集描述：使用两个真实的空气质量数据集进行实验，以评估所提出的模型性能。北京，从UCI机器学习存储库收集的多站点空气质量数据集用作基线数据集；另一个数据集从印度中央污染控制委员会收集也用于模型评估。

以 0.1 的概率添加了 dropout，避免过度拟合问题。Epochs大小为 2000，batch大小为 32，预测区域设置为 14 ，以进行长期空气质量预测。Relu 用作激活函数。RMSProp 为所有模型的优化器。它考虑以前的权重更新以更新下一个权重，而不是仅考虑当前的梯度值。MAE作为所有模型的默认损失函数，因为它可以更好地反映预测误差的实际情况。此外，在训练所有模型之前，利用 Z -score归一化过程对数据集进行归一化并删除异常值。均方根误差（RMSE）和平均绝对误差（MAE）用作模型评估指标。

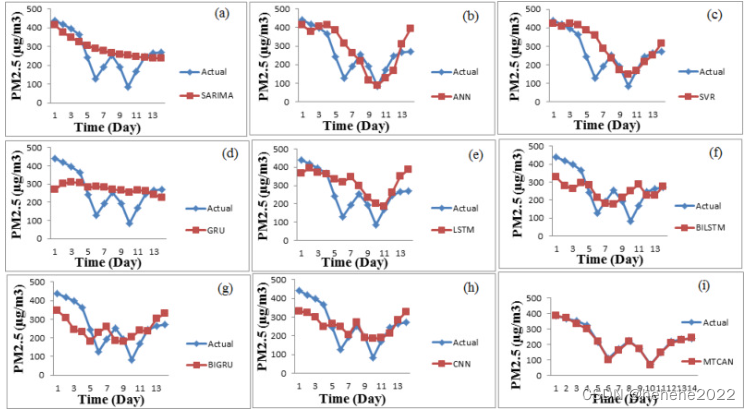在这里插入图片描述上图显示了八个基线模型和MTCAN模型的预测比较结果。

结论

本文提出了一种新的深度学习架构，该架构利用数据插补方法来插补气象和污染物值，而不会失去它们的相关性。该模型可以利用气象因子与PM10污染物的时间相关性来估算PM2.5缺失值。同时，我们通过TCN模型的膨胀卷积特征考虑了大量历史数据集，以进行长期时间预测。结果表明，所提模型同时解决了所有讨论的问题，并最大限度地减少了空气质量建模的预测误差。

元胞自动机

元胞自动机是什么？

元胞自动机（cellular automata，CA）是一种时间、空间、状态都离散，空间相互作用和时间因果关系为局部的网格动力学模型，具有模拟复杂系统时空演化过程的能力。

构成及规则

元胞自动机的组成：元胞，元胞空间，元胞邻居，元胞边界，规则。
元胞：又称细胞、单元或者基元，是元胞自动机最基本的组成部分，元胞自动机变化的载体。
自动机：通过对元胞设定规则，每个元胞状态会不断自动更新。
元胞空间：元胞在空间分布上的集合。
元胞邻居：元胞自动机的演化规则是局部的，对于指定元胞的状态进行更新时只需要知道其临近元胞的状态；元胞的状态受自身状态和周围邻居的影响。

某一元胞状态更新时搜索的空间域（常见的几种）：
冯.诺伊曼邻居（4邻居型）：
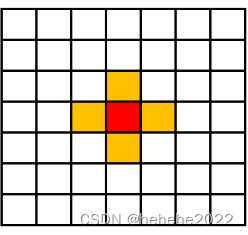
在这里插入图片描述
红色方格是中心元胞，周围是4个邻居。
摩尔型邻居（8邻居型）

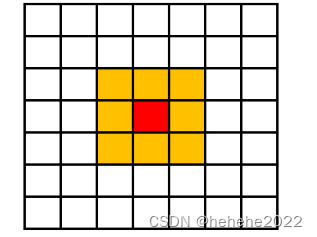
扩展摩尔型邻居（24邻居型）

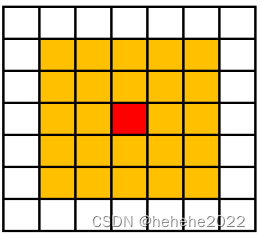
元胞规则：根据元胞当前状态及其邻居状态确定下一时刻该元胞状态。演化规则是元胞自动机的灵魂所在。
元胞边界：元胞自动机对每个元胞施加同样的规则，因此要设置边界条件，使边界上的细胞与其他细胞具有相同的邻居数目。
边界类型：
固定边界：所有边界外元胞均取某一固定常量。
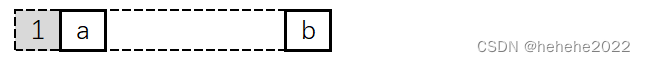
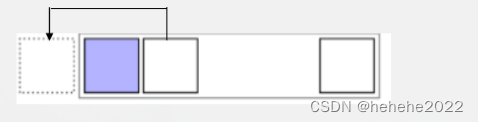
在这里插入图片描述
周期型边界：周期型是指相对边界连接起来的元胞空间。这种空间与无限空间最为接近，进行理论探讨时，常以此类空间作为实验进行模拟。

绝热边界：边界外元胞的状态始终和边界元胞的状态保持一致。
在这里插入图片描述
映射型边界：以边界元胞为对称轴的元胞状态作为边界。

案例及代码实现

生命游戏

每个格子的生死遵循下面的原则：
1．如果一个细胞周围有3个细胞为生（一个细胞周围共有8个细胞），则该细胞为生（即该细胞若原先为死，则转为生，若原先为生，则保持不变）。
2．如果一个细胞周围有2个细胞为生，则该细胞的生死状态保持不变；
3．在其它情况下，该细胞为死（即该细胞若原先为生，则转为死，若原先为死，则保持不变）

代码实现：

%生命游戏---元胞自动机
%每个格子的生死遵循下面的原则： 
%1． 如果一个细胞周围有3个细胞为生（一个细胞周围共有8个细胞），则该细胞为生（即该细胞若原先为死，则转为生，若原先为生，则保持不变） 。 
%2． 如果一个细胞周围有2个细胞为生，则该细胞的生死状态保持不变； 
%3． 在其它情况下，该细胞为死（即该细胞若原先为生，则转为死，若原先为死，则保持不变） 

function ca
m=10;n=10;%世界大小m*n
p=.7;%用于初始化生命(p理解为为每一点出现生命的概率)
h=1000;%h为生命游戏进行的轮数

%生命的随机初始化设定(前两重循环)
for x=1:m %对网格点的初始化
    for y=1:n
        r=rand(1); %r为U[0,1]中随机产生的一个数字   rand(1)中的1代表矩阵r的规模为1*1即一个数
        if r>p
            a(x,y)=1;
        else
            a(x,y)=0;
        end
    end
end
for x=1:m%根据网格初始化后的结果来进行网格生命初始化设定
    for y=1:n
        if a(x,y)==1 %如果网格点(x,y)为1,则生命方块(x-1,y-1) (x-1,y) (x,y-1) (x,y)赋予生命
            fx=[x-1,x-1,x,x];
            fy=[y-1,y,y,y-1];
            fill(fx,fy,'g')%填涂绿色表示获得生命
            hold on
        else %否则保持不变,即不获得生命
        end
    end
end


for k=1:h %一共进行h轮生命游戏
    fx=[0,m,m,0];
    fy=[0,0,n,n];
    fill(fx,fy,'k'),%新的一轮开始,将所有的格子全部涂黑,按上一轮得到的新的a来重新涂色,便于观察
    hold on
    
    for x=2:m-1%遍历每一个点
        for y=2:n-1
            %b(x,y)为点a(x,y)附近八个点的和
            b(x,y)=a(x-1,y-1)+a(x-1,y)+a(x-1,y+1)+a(x,y-1)+a(x,y+1)+a(x+1,y-1)+a(x+1,y)+a(x+1,y+1);
            if b(x,y)==2 %如果a(x,y)附近有两个点,a(x,y)保持不变
                c(x,y)=a(x,y);
            elseif b(x,y)==3,%如果a(x,y)附近有三个点,a(x,y)获得生命
                c(x,y)=1;
            else         %否则,a(x,y)失去生命
                c(x,y)=0;
            end
        end
    end
    %a的第一列和最后一列保持不变,因为上面的循环是从x=2:m-1 y=2:n-1
    c(1:m,1)=a(1:m,1);
    c(1:m,n)=a(1:m,n);
    
    for x=1:m %根据这一轮点的生命情况来确定它左下角这个格子的生命情况
        for y=1:n
            if c(x,y)==1
                fx=[x-1,x-1,x,x];
                fy=[y-1,y,y,y-1];
                fill(fx,fy,'g')
                hold on
            else
            end
        end
    end
pause(0.01)%停止0.02秒后开始下一轮
a=c;
end