电子技术——分析放大器的高频响应的有用工具

在前几章我们使用米勒效应估计了CS和CE放大器模型的高频响应 f H f_H fH ,以及分析了其限制和影响因素。然而,这个方法不能有效的处理负载是容性负载 C L C_L CL 的情况。同时,这个方法不能扩展到更复杂的电路。对此,我们本节介绍一些分析放大器的高频响应的有用工具,用来分析更加复杂的电路,例如共源共栅放大器。
高频增益函数
考虑到内部电容的放大器的增益,能够被表示为:
A ( s ) = A M F H ( s ) A(s) = A_MF_H(s) A(s)=AMFH(s)
其中 A M A_M AM 是中频带增益,通过将所有的电容效应忽略,我们可以计算出 A M A_M AM 。将电容效应考虑进去之后,我们乘以增益因子 F H ( s ) F_H(s) FH(s) ,能够被表示为带有多个零点和极点(一般都是实数)的复数多项式:
F H ( s ) = ( 1 + s / ω Z 1 ) ( 1 + s / ω Z 2 ) … ( 1 + s / ω Z n ) ( 1 + s / ω P 1 ) ( 1 + s / ω P 2 ) … ( 1 + s / ω P n ) F_H(s) = \frac{(1 + s/ \omega_{Z1}) (1 + s/ \omega_{Z2}) \ldots (1 + s/ \omega_{Zn})}{(1 + s/ \omega_{P1}) (1 + s/ \omega_{P2}) \ldots (1 + s/ \omega_{Pn})} FH(s)=(1+s/ωP1)(1+s/ωP2)…(1+s/ωPn)(1+s/ωZ1)(1+s/ωZ2)…(1+s/ωZn)
这里 ω P 1 , ω P 2 , … , ω P n \omega_{P1},\omega_{P2},\ldots,\omega_{Pn} ωP1,ωP2,…,ωPn 都是正数,代表了 n n n 个实极点。这里 ω Z 1 , ω Z 2 , … , ω Z n \omega_{Z1},\omega_{Z2},\ldots,\omega_{Zn} ωZ1,ωZ2,…,ωZn 是正数、负数或是无穷,代表了 n n n 个实传输零点。因为通常情况下,零点和极点的频率都大于中频带,因此当 s s s 接近于中频带的时候, F H ( s ) F_H(s) FH(s) 接近于一。
决定 − 3 d B -3dB −3dB 频率 f H f_H fH
若在传递函数中,存在一个极点频率 ω P 1 \omega_{P1} ωP1 小于其他的极点频率,那么这个极点将决定放大器的高频响应频率 f H f_H fH 。我们称这个放大器是有 主极点响应 的。因此,其频率响应因子可以近似的表示为:
F H ( s ) ≃ 1 1 + s / ω P 1 F_H(s) \simeq \frac{1}{1 + s / \omega_{P1}} FH(s)≃1+s/ωP11
这是一个STC的低通型网络模型,同时:
ω H ≃ ω P 1 \omega_H \simeq \omega_{P1} ωH≃ωP1
我们之前的CS和CE放大器的分析就是用这个法则进行近似的,另外存在一个我们之前使用过的经验法则:当最低频率极点至少是最近极点或零点的 1 / 4 1/4 1/4 倍的时候,主极点存在。
若主极点不存在,我们可以绘制 ∣ F H ( s ) ∣ |F_H(s)| ∣FH(s)∣ 的图像。或者,通过下面的估算方法:
为了方便,我们假设我们有两个极点和零点。
F H ( s ) = ( 1 + s / ω Z 1 ) ( 1 + s / ω Z 2 ) ( 1 + s / ω P 1 ) ( 1 + s / ω P 2 ) F_H(s) = \frac{(1 + s/ \omega_{Z1}) (1 + s/ \omega_{Z2})}{(1 + s/ \omega_{P1}) (1 + s/ \omega_{P2})} FH(s)=(1+s/ωP1)(1+s/ωP2)(1+s/ωZ1)(1+s/ωZ2)
带入 s = j ω s = j\omega s=jω 。
∣ F H ( s ) ∣ 2 = ( 1 + ω 2 / ω Z 1 2 ) ( 1 + ω 2 / ω Z 2 2 ) ( 1 + ω 2 / ω P 1 2 ) ( 1 + ω 2 / ω P 2 2 ) |F_H(s)|^2 = \frac{(1 + \omega^2/ \omega_{Z1}^2) (1 + \omega^2/ \omega_{Z2}^2)}{(1 + \omega^2/ \omega_{P1}^2) (1 + \omega^2/ \omega_{P2}^2)} ∣FH(s)∣2=(1+ω2/ωP12)(1+ω2/ωP22)(1+ω2/ωZ12)(1+ω2/ωZ22)
根据定义, ω = ω H \omega = \omega_H ω=ωH 当 ∣ F H ∣ 2 = 1 / 2 |F_H|^2 = 1/2 ∣FH∣2=1/2 因此:
1 / 2 = ( 1 + ω H 2 / ω Z 1 2 ) ( 1 + ω H 2 / ω Z 2 2 ) ( 1 + ω H 2 / ω P 1 2 ) ( 1 + ω H 2 / ω P 2 2 ) = 1 + ω H 2 ( 1 ω Z 1 2 + 1 ω Z 2 2 ) + ω H 4 / ω Z 1 2 ω Z 2 2 1 + ω H 2 ( 1 ω P 1 2 + 1 ω P 2 2 ) + ω H 4 / ω P 1 2 ω P 2 2 1/2 = \frac{(1 + \omega_H^2/ \omega_{Z1}^2) (1 + \omega_H^2/ \omega_{Z2}^2)}{(1 + \omega_H^2/ \omega_{P1}^2) (1 + \omega_H^2/ \omega_{P2}^2)} = \frac{1 + \omega_H^2(\frac{1}{\omega_{Z1}^2} + \frac{1}{\omega_{Z2}^2}) + \omega_H^4/\omega_{Z1}^2\omega_{Z2}^2}{1 + \omega_H^2(\frac{1}{\omega_{P1}^2} + \frac{1}{\omega_{P2}^2}) + \omega_H^4/\omega_{P1}^2\omega_{P2}^2} 1/2=(1+ωH2/ωP12)(1+ωH2/ωP22)(1+ωH2/ωZ12)(1+ωH2/ωZ22)=1+ωH2(ωP121+ωP221)+ωH4/ωP12ωP221+ωH2(ωZ121+ωZ221)+ωH4/ωZ12ωZ22
因为 ω H \omega_H ωH 通常小于其他极点和零点,因此我们可以忽略四次项,解得:
ω H = 1 / 1 ω P 1 2 + 1 ω P 2 2 − 2 ω Z 1 2 − 2 ω Z 2 2 \omega_H = 1 / \sqrt{\frac{1}{\omega_{P1}^2} + \frac{1}{\omega_{P2}^2} - \frac{2}{\omega_{Z1}^2} - \frac{2}{\omega_{Z2}^2}} ωH=1/ωP121+ωP221−ωZ122−ωZ222
可以扩展到任意个数的极点和零点:
ω H = 1 / 1 ( ω P 1 2 + 1 ω P 2 2 + … ) − 2 ( 1 ω Z 1 2 + 1 ω Z 2 2 + … ) \omega_H = 1 / \sqrt{\frac{1}{(\omega_{P1}^2} + \frac{1}{\omega_{P2}^2} + \ldots) - 2( \frac{1}{\omega_{Z1}^2} + \frac{1}{\omega_{Z2}^2} + \ldots)} ωH=1/(ωP121+ωP221+…)−2(ωZ121+ωZ221+…)
开路时间常数法
如果可以计算出所有的零点和极点,我们可以使用上述的估算方法。但是有时候计算零点和极点是困难的,我们可以使用开路时间常数法。这个方法和我们在之前估算低频响应时候使用的短路时间常数法是对偶方法。
首先频率因子可以写作为:
F H ( s ) = 1 + a 1 s + a 2 s 2 + … + a n s n 1 + b 1 s + b 2 s 2 + … + b n s n F_H(s) = \frac{1 + a_1s + a_2s^2 + \ldots + a_ns^n}{1 + b_1s + b_2s^2 + \ldots + b_ns^n} FH(s)=1+b1s+b2s2+…+bnsn1+a1s+a2s2+…+ansn
这里系数 a a a 和 b b b 由极点和零点共同确定。实际上:
b 1 = 1 ω P 1 + 1 ω P 2 + … + 1 ω P n b_1 = \frac{1}{\omega_{P1}} + \frac{1}{\omega_{P2}} + \ldots + \frac{1}{\omega_{Pn}} b1=ωP11+ωP21+…+ωPn1
可以证明 b 1 b_1 b1 等于将信号源置零,然后依次考虑每一个电容,当考虑到第 i i i 个电容的时候,将其他电容视为开路,然后计算从这个电容看过去的等效戴维南电阻 R i R_i Ri 我们记电容 i i i 对应的时间常数为 τ i = C i R i \tau_i = C_i R_i τi=CiRi 。给出 b 1 b_1 b1 :
b 1 = ∑ i = 1 n C i R i b_1 = \sum_{i=1}^n C_i R_i b1=i=1∑nCiRi
称为 开路时间常数 。
假设存在一个主导的极点频率,那么:
b 1 ≃ 1 ω P 1 b_1 \simeq \frac{1}{\omega_{P1}} b1≃ωP11
也就是:
ω H ≃ 1 ∑ i = 1 n C i R i \omega_H \simeq \frac{1}{\sum_{i=1}^n C_i R_i} ωH≃∑i=1nCiRi1
当不存在主导的极点频率的时候,上述方法也能意外的得到较好的估计结果。
应用开路时间常数法分析CS放大器
下图展示了一个CS放大器的高频模型:
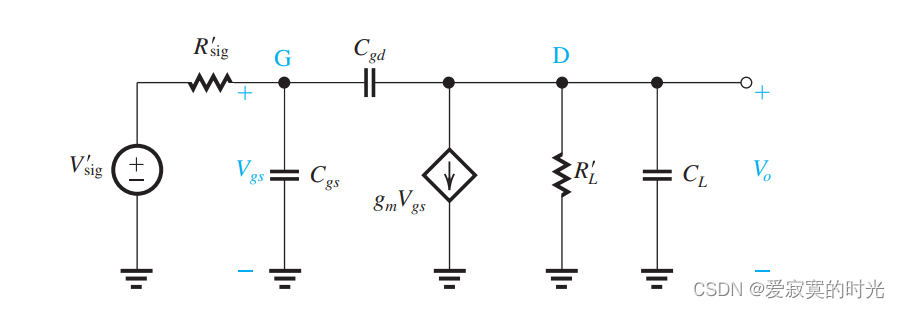
我们对其使用开路时间常数法,首先我们我们先让
V
s
i
g
=
0
V_{sig} = 0
Vsig=0 ,依次考虑每一个电容,并将其他电容开路:
首先考虑电容 C g s C_{gs} Cgs :
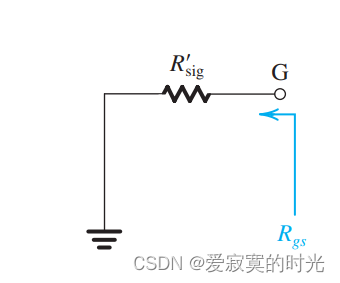
R
g
s
=
R
s
i
g
′
R_{gs} = R_{sig}'
Rgs=Rsig′
接下来考虑电容 C g d C_{gd} Cgd :
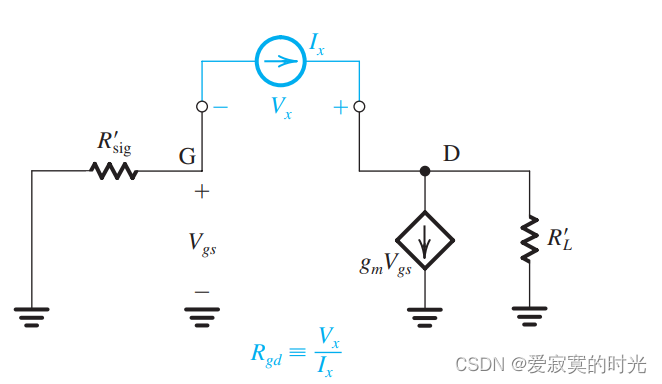
使用戴维南定理得到:
R g d = R s i g ′ ( 1 + g m R L ′ ) + R L ′ R_{gd} = R_{sig}'(1 + g_m R_L') + R_L' Rgd=Rsig′(1+gmRL′)+RL′
最后考虑电容 C L C_L CL :
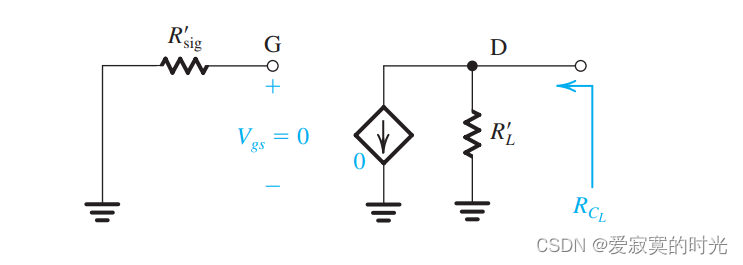
R C L = R L ′ R_{CL} = R_L' RCL=RL′
最后总短路时间常数为:
τ H = b 1 = C g s R g s + C g d R g d + C L R C L \tau_H = b_1 = C_{gs}R_{gs} + C_{gd}R_{gd} + C_L R_{CL} τH=b1=CgsRgs+CgdRgd+CLRCL
则:
f H = 1 2 π τ H f_H = \frac{1}{2 \pi \tau_H} fH=2πτH1
我们发现:
τ H = [ C g s + C g d ( 1 + g m R L ′ ) ] R s i g ′ + ( C g d + C L ) R L ′ \tau_H = [C_{gs} + C_{gd}(1 + g_m R_L')]R_{sig}' + (C_{gd} + C_L)R_L' τH=[Cgs+Cgd(1+gmRL′)]Rsig′+(Cgd+CL)RL′
我们发现第一个项可以写作是 C i n R s i g ′ C_{in}R_{sig}' CinRsig′ 其中 C i n C_{in} Cin 是米勒等效后的输入电容。后一项是引入 C L C_L CL 和 C g d C_{gd} Cgd 后的影响因素。我们发现若当 R s i g ′ R_{sig}' Rsig′ 较大的时候,后一项可以忽略。
最后一点,开路时间常数法让我们知道了决定 f H f_H fH 各种因素的占比,通常, C g d C_{gd} Cgd 贡献了 62 % 62\% 62% (米勒效应)。而 C g s C_{gs} Cgs 贡献了 17 % 17\% 17% 以及 C L C_L CL 贡献了 12 % 12\% 12% 。
应用开路时间常数法分析CE放大器
CE放大器和CS放大器的模型基本一致,读者可以自行尝试。