一、图的引入

1.引言

       图论发源于十八世纪，最早主要研究一些游戏问题：如哥尼斯堡七桥问题，迷宫问题和博弈问题等。计算机出现以后，图论得到了长足的发展，至今仍然活跃在科研和实际应用的第一线，如现在受到普遍关注的云计算，大数据应用和深度学习等。

2.不同类型的图

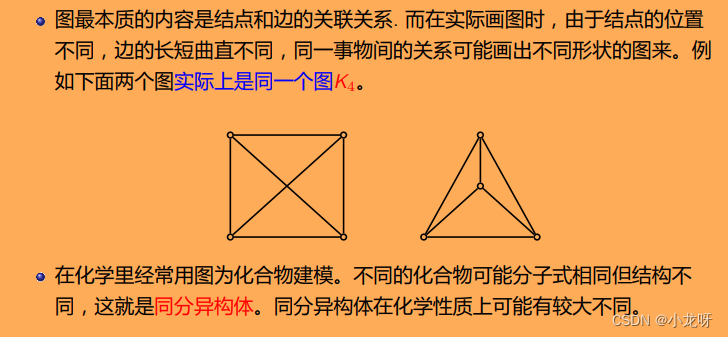
       图论所讨论的图(Graph)与人们通常所熟悉的图(如圆、椭圆、函数图表等)是很不相同的，图论中的图是指某类具体离散事物集合和该集合中的每对事物间以某种方式相联系的数学模型。
下面给出一些例子：

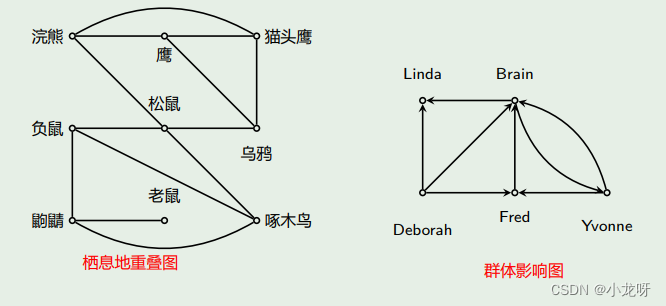
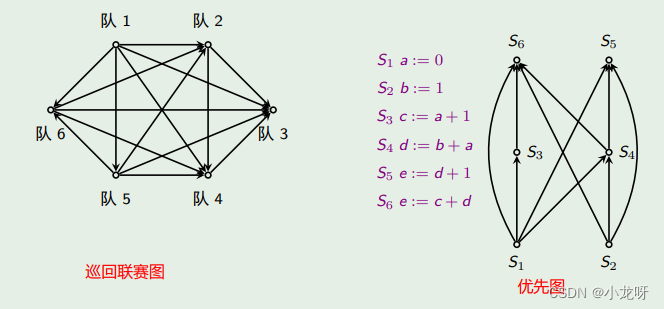
3.无序对和无序积

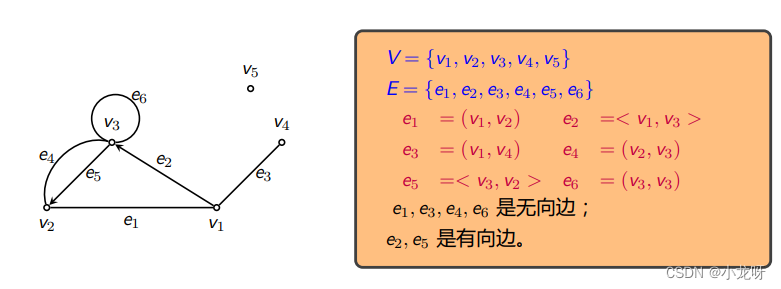
4.什么是图

二、图的表示

1.图的表示

       对于一个图 G，如果将其记为 G =< V, E >，并写出 V 和 E 的集合表示，这称为图的集合表示。
为了描述简便起见，在一般情况下，往往只画出它的图形：用小圆圈表示 V 中的结点，用由 u 指向 v 的有向线段或曲线表示有向边 < u, v >，无向线段或曲线表示无向边 (u, v)，这称为图的图形表示。

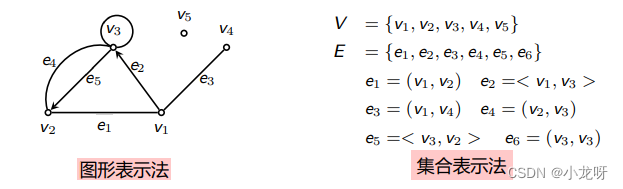
       图形表示法的优点是形象直观，但不适合于大图，而集合表示法的优点是精确，但抽象不易理解。为了便于用代数知识来研究图的性质，特别是便于用计算机来处理，我们引入图的矩阵表示。因为矩阵的存储和处理在计算机中是非常容易的，从而能够把图的问题变为数字计算问题，再利用矩阵代数的运算来计算图的通路、回路和其它特征。

2.邻接矩阵

3.邻接点与邻接边

       在图 G =< V, E > 中，若两个结点 $v_i$ 和 $v_j$ 是边 e 的端点，则称 $v_i$ 与 $v_j$ 互为邻接点，否则 $v_i$ 与 $v_j$ 称为不邻接的；具有公共结点的两条边称为邻接边；两个端点相同的边称为环或自回路；图中不与任何结点相邻接的结点称为孤立结点。

4.一些简单的特殊图

       仅由孤立结点组成的图称为零图；仅含一个结点的零图称为平凡图；含有 n 个结点，m 条边的图，称为(n, m)图。

• 环的存在与否不会导致图论定理的重大变化，很多场合下都会被忽略；
• 零图没有任何边，邻接矩阵为全 0；
• (8,20)图表示一个图有8个结点，20 条边，但图的各边如何分布则不清楚。

三、图的分类

1.按边有无方向分类

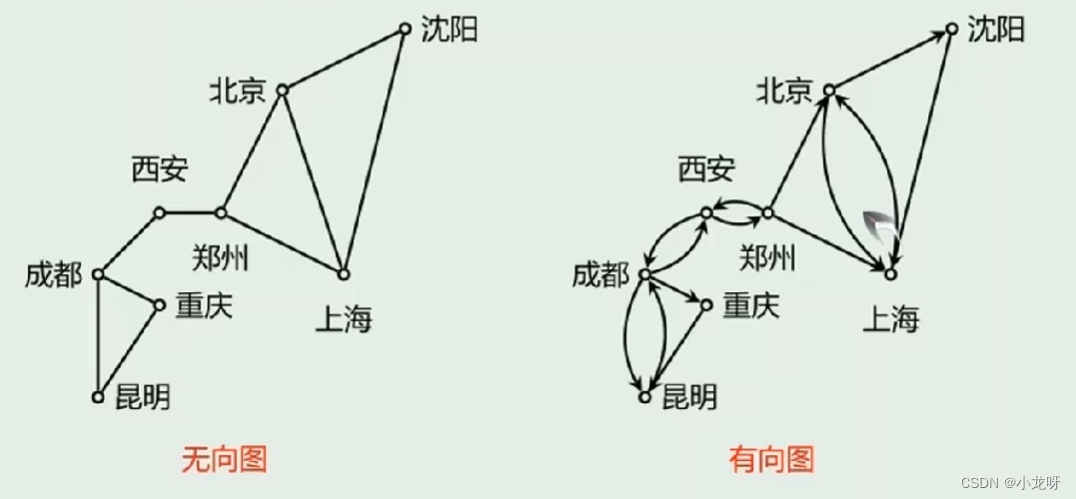
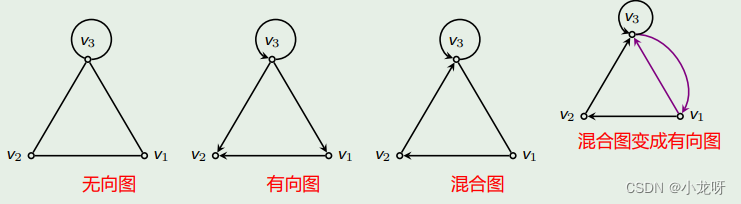
       每条边都是无向边的图称为无向图(undirected graph)；每条边都是有向边的图称为有向图(directed graph)；有些边是无向边，而另一些边是有向边的图称为混合图(mixed graph)。

2.按有无平行边分类

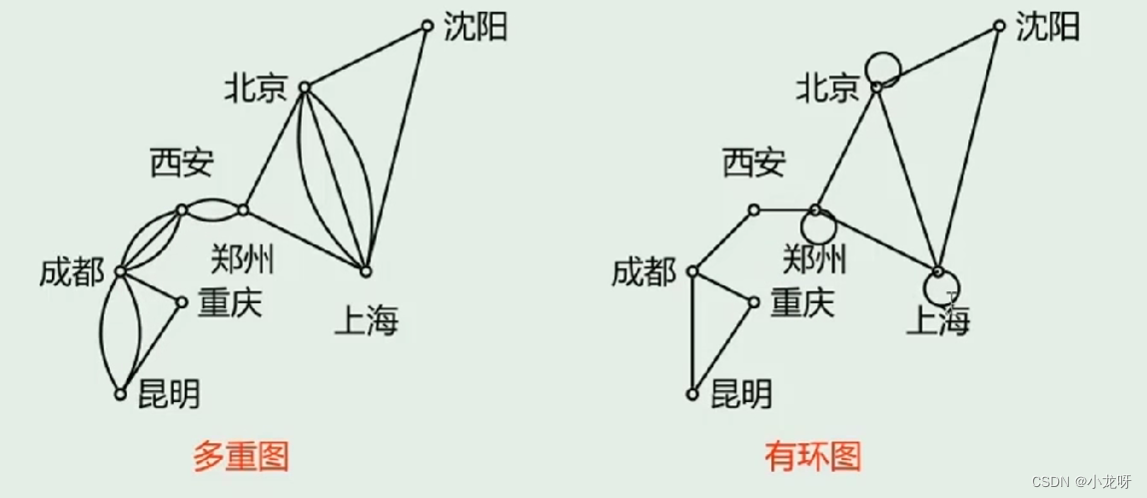
       在有向图中，两结点间 (包括结点自身间) 若有同始点和同终点的几条边，则这几条边称为平行边；在无向图中，两结点间(包括结点自身间)若有几条边，则这几条边称为平行边。两结点 a、b 间相互平行的边的条数称为边 (a, b) 或 <a, b> 的重数。含有平行边的图称为多重图(multigraph)；非多重图称为线图(line graph)；无环的线图称为简单图(simple graph)。

3.按有无权值分类

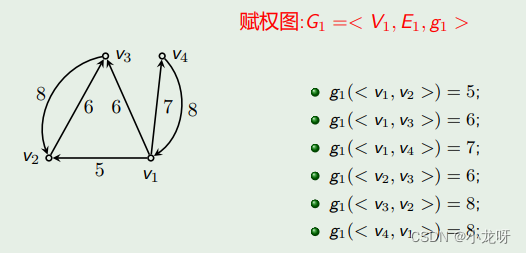
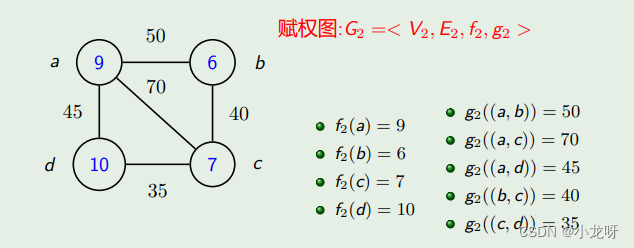
       赋权图(weighted graph)G 是一个三重组 < V, E, g > 或四重组 < V, E, f, g >，其中 V 是结点集合，E 是边的集合，f 是从 V 到非负实数集合的函数（即结点的权值函数），g 是从 E 到非负实数集合的函数（即边的权值函数）。相应的，边或结点均无权值的称为无权图。

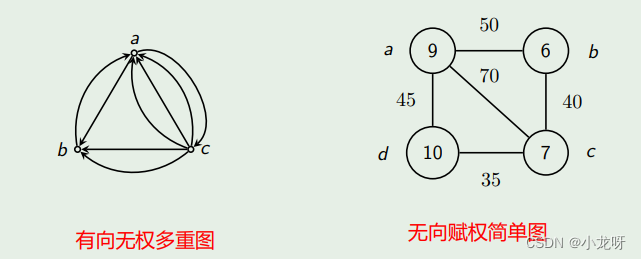
4.综合分类方法

       可将以上三种分类方法综合起来对图进行划分。

四、子图和补图

1.各类子图

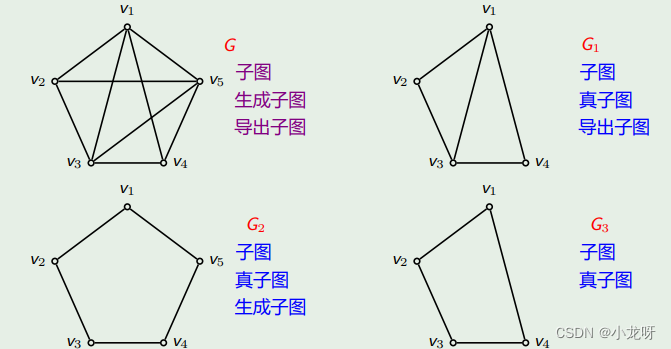
2.完全图

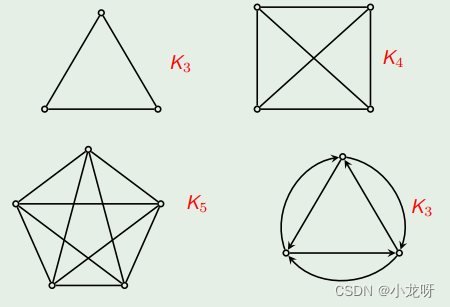
3.补图

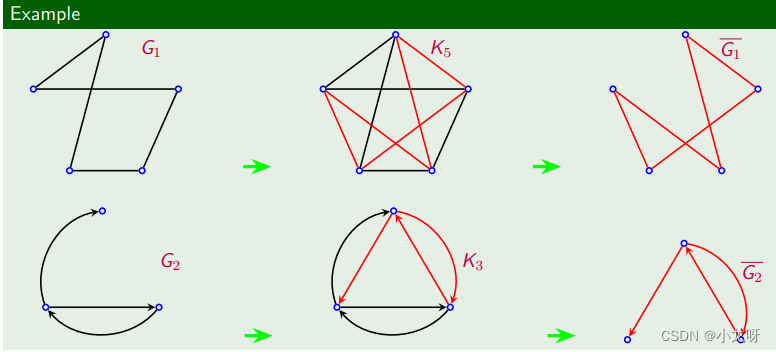
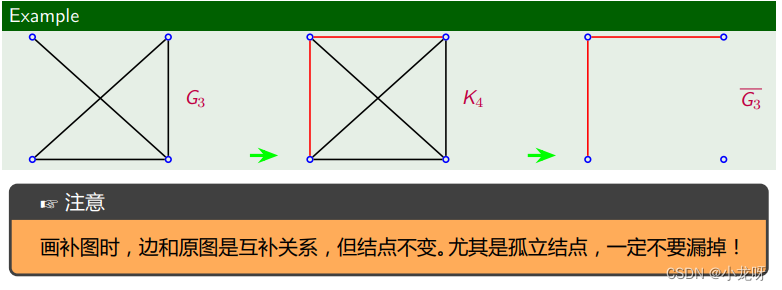
4.补图的邻接矩阵

5.补图的应用

五、握手定理

1.结点的度数

2.邻接矩阵计算度数

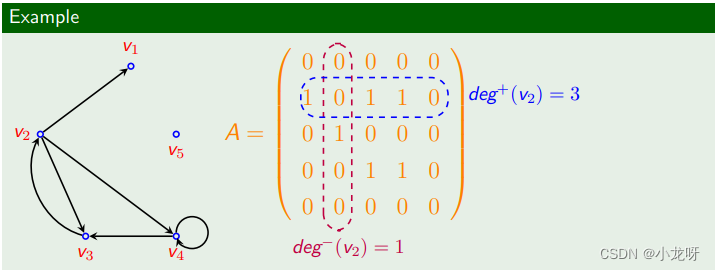
3.握手定理

4.握手定理推论

5.图的度数序列

       设 V = {v1, v2, · · · , vn} 为图 G 的结点集，称 (deg($v_1$), deg($v_2$), · · · , deg($v_n$)) 为 G 的度数序列。若 G 为有向图，还可分别定义出度序列和入度序列。

六、图的同构

1.引言

2.图的同构

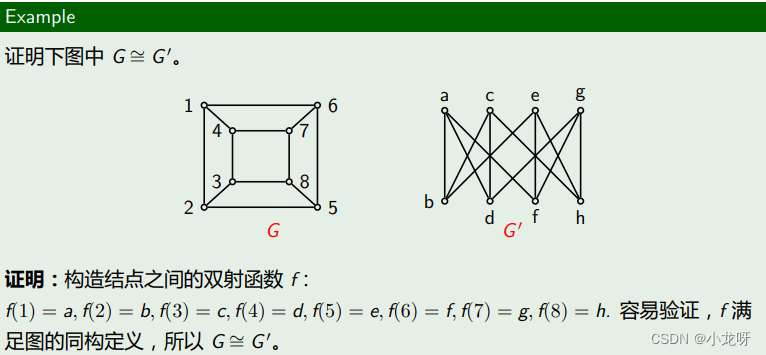
       判定同构的方法关键就是找到结点间的对应关系，而在两个带有 n 个结点的图之间有 n! 种可能的一一对应关系。尤其是当 n 很大时，判断任意两个图是否同构常常是一件困难的事情。

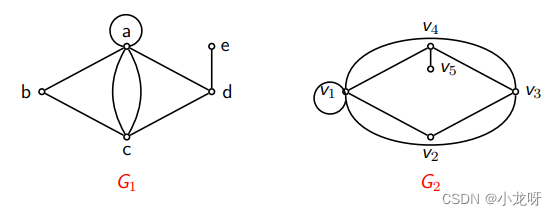
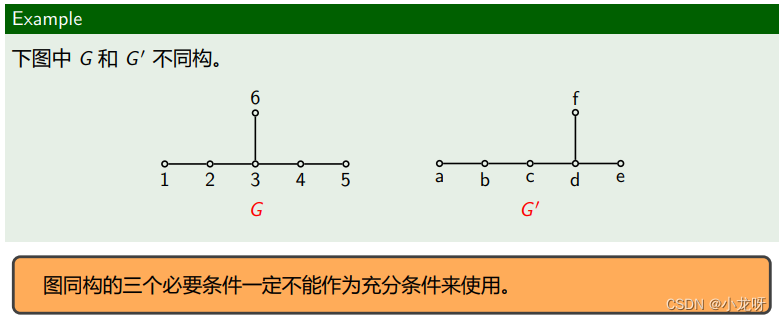
3.图同构的必要条件

本文内容参考：
中国大学慕课电子科技大学《离散数学》
如有错误或者不足之处，欢迎大家留言指正！