题目描述
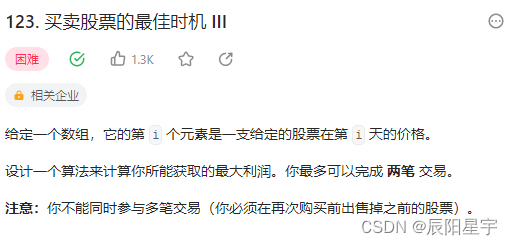


原题链接:123. 买卖股票的最佳时机 III
解题思路
(1)二维dp数组
- 动态规划五步曲:
(1)dp数组含义: dp[i][0],表示无操作。主要由四个状态来表示四种操作。dp[i][1],表示在第i天时,已经第一次持有过股票时,具有的最大收益。dp[i][2],表示在第i天时,已经第一次不持过有股票票时,具有的最大收益。dp[i][3],表示在第i天时,已经第二次持有过股票票时,具有的最大收益。dp[i][4],表示在第i天时,已经第二次不持有过股票票时,具有的最大收益。
(2)递推公式:
-
dp[i][1] = max(dp[i - 1][1], -prices[i]),表示在之前已第一次持有股票和第i天第一次持有股票中,找一个最大值,作为最大收益。
-
dp[i][2] = max(dp[i - 1][2], dp[i][1] + prices[i]),表示在之前已第一次不持有股票和第i天把股票售出后中,找一个最大值,作为最大收益。
-
dp[i][3] = max(dp[i - 1][3], dp[i][2] + prices[i]),表示在之前已第二次不持有股票和第i天第二次持有股票中,找一个最大值,作为最大收益。这里注意,第i天时,第二次持有股票要从第一次不持有股票(第一次售出股票)后的状态得来。
-
dp[i][4] = max(dp[i - 1][4], dp[i][3] + prices[i]),表示在之前已第二次不持有股票和第i天把股票售出后中,找一个最大值,作为最大收益。
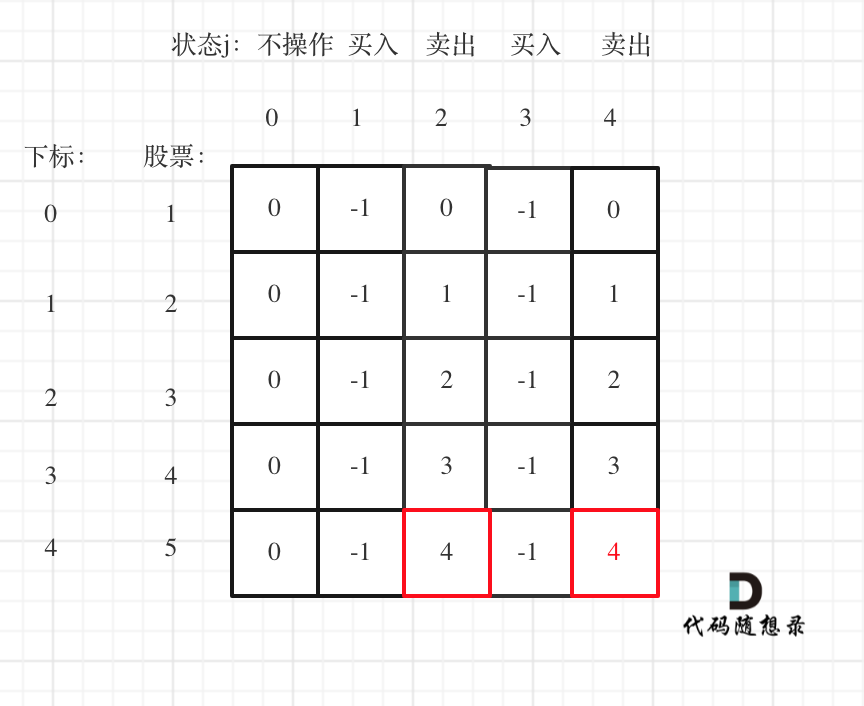
(3)dp数组初始化: dp[0][0] = 0,遍历后续计算。dp[0][1] = -prices[0],第一天购买股票,总收益减去当天股价。dp[0][2] = 0,第一次不持有,就相当于当天买当天卖。dp[0][3] = -prices[0],第二次购买股票,相当于第一天买卖后,又买一次。dp[0][4] = 0,第二次卖出。
(4)遍历顺序: 从小到大。
(5)举例:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int>> dp(n + 1, vector<int>(5));
dp[0][0] = 0;
dp[0][1] = -prices[0], dp[0][2] = 0;
dp[0][3] = -prices[0], dp[0][4] = 0;
for(int i = 1; i < n; i++) {
dp[i][1] = max(dp[i - 1][1], - prices[i]);
dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
}
return dp[n - 1][4];
}
};
(2)变量优化一维dp数组
-
dp[i][1] = max(dp[i - 1][1], - prices[i])主要取决于i-1时情况和当下买入情况,可优化为dp[1] = max(dp[1], - prices[i]),每次到第i次遍历时,max中的dp[1]就相当于是第i-1次时计算得到的结果,取完最大值后,dp[1]就变为了dp[i][1] -
dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]),同上取决于dp[i-1][2]和dp[i-1][prices[i]],可优化为dp[2] = max(dp[2], dp[1] + prices[i])。如果是dp[i-1][2]大的话,直接得出即可。如果是dp[i-1][prices[i]]大的话,若上一条代码执行的是dp[i][1]=-prices[i],此时若再次执行该条代码就会在同一天进行依次买卖,最终变为0。但在实际代码运行中并不会这样执行,除非prices数组中都为0。 -
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]),同理可优化为dp[3] = max(dp[3], dp[2] - prices[i])。 -
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]),同理可优化为dp[4] = max(dp[4], dp[3] + prices[i])。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<int> dp(5);
dp[0] = 0;
dp[1] = -prices[0], dp[2] = 0;
dp[3] = -prices[0], dp[4] = 0;
for(int i = 1; i < n; i++) {
dp[1] = max(dp[1], - prices[i]);
dp[2] = max(dp[2], dp[1] + prices[i]);
dp[3] = max(dp[3], dp[2] - prices[i]);
dp[4] = max(dp[4], dp[3] + prices[i]);
}
return dp[4];
}
};
参考文章:123. 买卖股票的最佳时机 III