生成模型

生成模型和判别模型的差异

生成模型的目标是在给定了数据集D，并且假设这个数据集的底层分布(underlying distribution)是Pdata，我们希望够近似出这个数据分布。如果我们能够学习到一个好的生成模型，我们就能用这个生成模型为下游任务做inference 推理。

下面我们简单回顾一下生成模型和判别模型，读者可以自行选择跳过这小节。

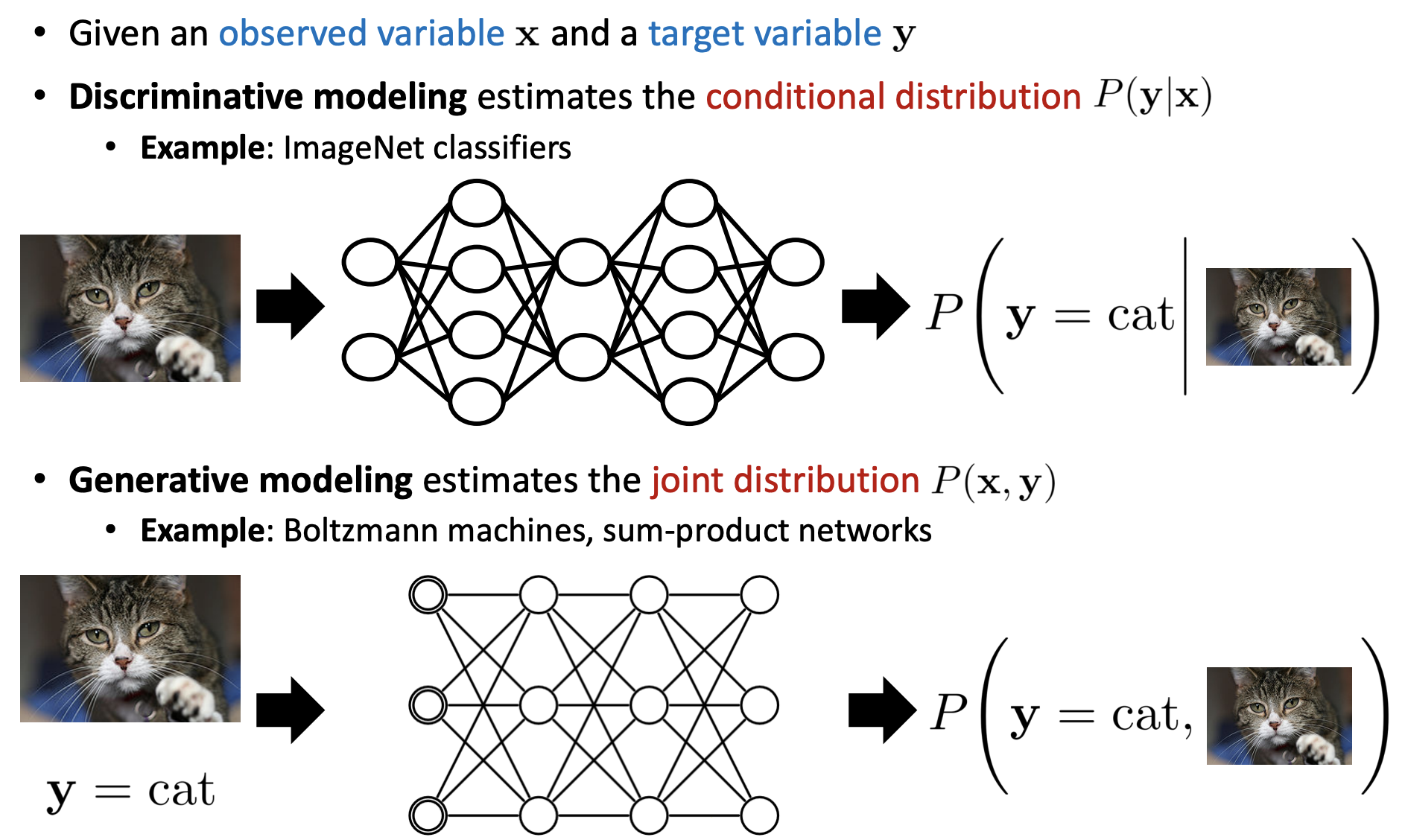
生成模型 VS 判别模型

对于判别模型(discriminative model)，像逻辑回归模型，是对给定的数据点预测一个标签label，但是对于生成模型，它学习的是整个数据的联合分布(joint distribution)。当然判别模型也可以理解为是给定了输入数据后，标签label的生成模型。但一般生成模型指的是高维数据。

那么如果我们的建模方式不一样，对应的模型也是不一样的。假设我们希望求 p(Y|X),对于左边的模型，我们需要用贝叶斯规则计算 p(Y) 和 p(X|Y)。而对于右边的模型，它已经可以直接用来计算 p(Y|X)， 因为 p(X) 是给定的，所以我们可以不用给它建模。

我们将随机变量在图上显示出来:

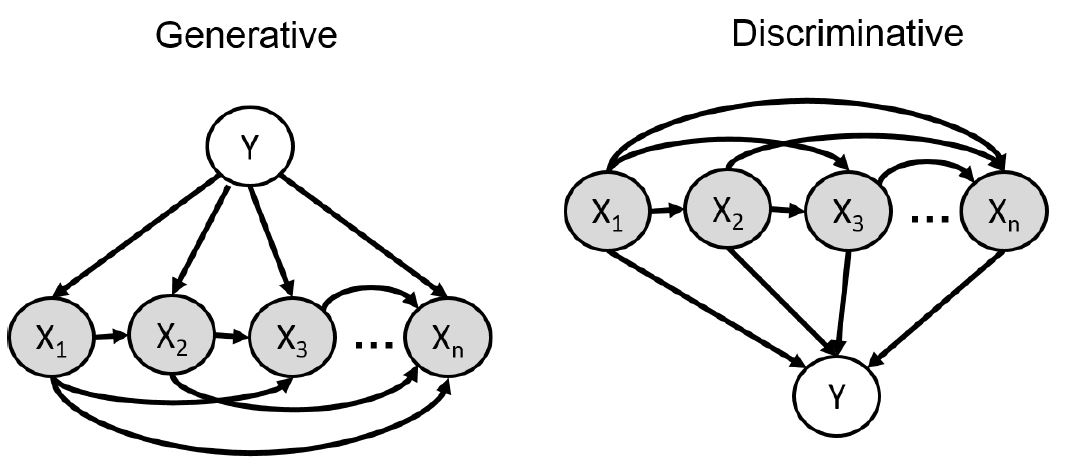
对于生成模型的联合分布: p(Y,X)=p(Y)p(X1|Y)p(X2|Y,X1)...p(Xn|Y,X1,…,Xn−1)我们需要考虑的是怎么确定 p(Xi|(X)pa(i),Y)的参数，这里的 pa(i)指的是指向随机变量 Xi的随机变量集合。

对于判别式模型的联合分布: p(Y,X)=p(X1)p(X2|X1)p(X3|X1,X2)...p(Y|X1,…,Xn)

生成模型例子-朴素贝叶斯

朴素贝叶斯(Naive Bayes)，它是生成模型的一个特例，它假设在给定了label之后，各个随机变量之间是独立的，这就是它 naive 的原因吧，如下图:

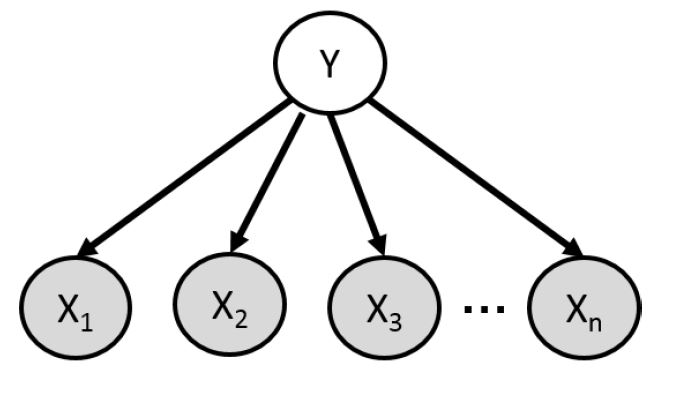
用训练数据估计参数，用贝叶斯规则做预测:

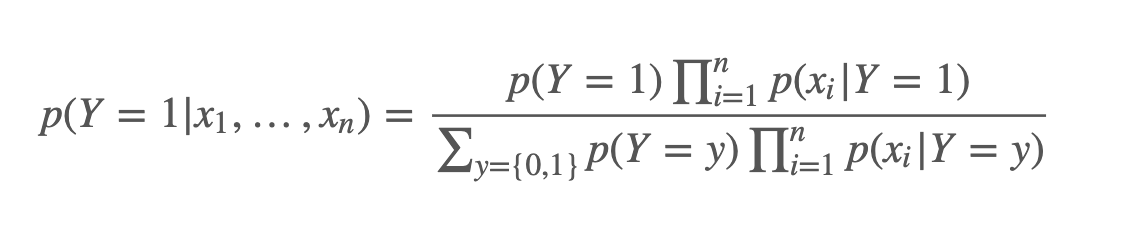
判别模型例子-逻辑回归

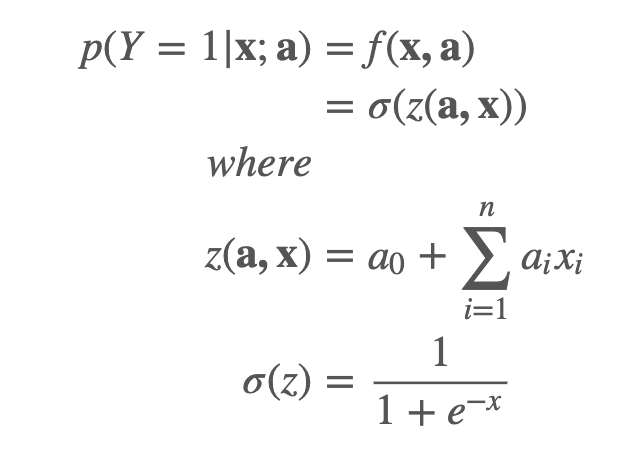
逻辑回归并不要求随机变量之间独立。

但是生成模型依然很有用，根据链式法则:

p(Y,X)=p(X|Y)p(Y)=p(Y|X)p(X)

假设 X的部分随机变量是可观测的，我们还是要计算 p(Y|Xevidence)，那么我们就可以对这些看不到的随机变量marginalize(积分求和)。

学习-Learning

生成模型的学习(learning)是指在给定一个数据分布 pdata和一个模型家族 (model family)的情况下，我们要从这个模型家族中找到一个近似分布pθ，使得它和数据分布尽可能的近。

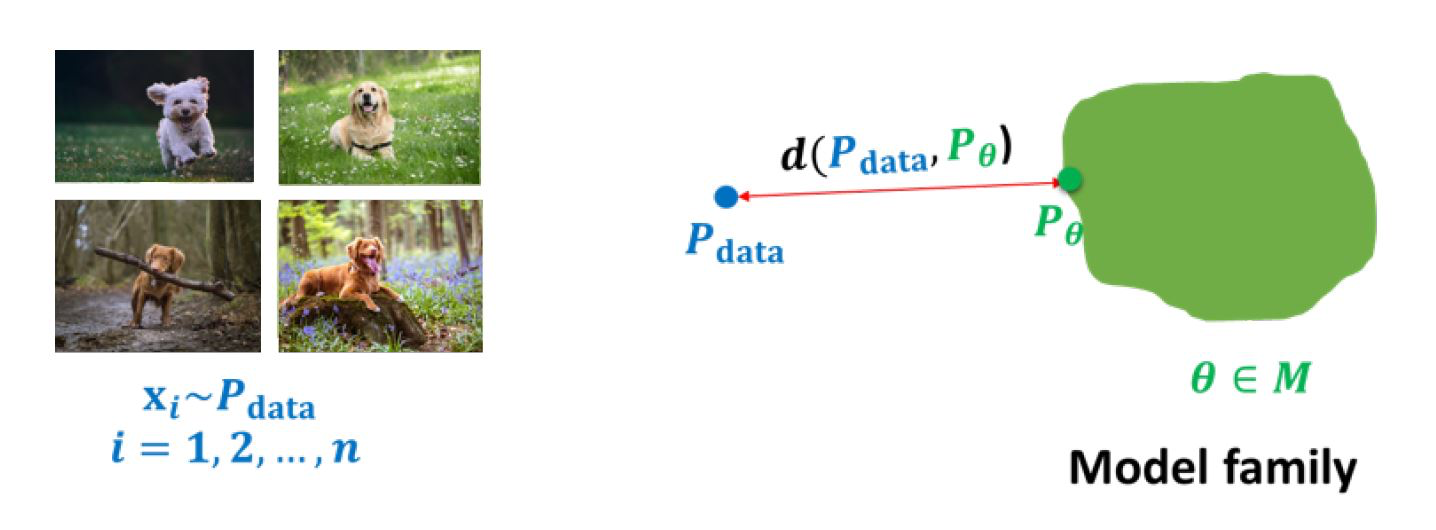
但是要怎么衡量这个近呢？我们用距离来衡量, 写成数学表达式:

minθ∈d(pdata,pθ)

因此，我们自然而然会对三个问题感兴趣:

模型家族M的表达式是神马？

1. 目标函数 d(⋅) 是什么样子的？

2. 最小化 d(⋅) 的优化过程是什么？

推理-Inference

一个生成模型应该是一个联合概率分布 p(x)，假设这个概率分布是从一堆狗狗的图片上学习到的，那么这个概率分布应该可以:

1. 生成(Generation), 即采样(sampling) xnew∼p(x)，并且采样 xnew图片应该很像狗狗。

2. 密度估计(Density estimation)，如果给了一张狗狗的图片 x，那么这个概率分布 p(x) 的值应该很高。或者给了一张不相关的图片，p(x)的值很低，这可以用来做异常检测。

3. 无监督表示学习(unsupervised representation learning), 我们可以学习到这些图片的一些公共信息，像是一些特征，耳朵，尾巴…

但我们也发现量化评估上面的任务1和任务3其实是很难的；其次，并不是所有的模型家族在这些任务上都推理速度都快且精准，也正是因为推理过程的折中和权衡，导致了各种不同的方法。

数学建模为随机分布，忽略了输入数据分布逐步转化到最后生成图片的随机过程，只关心输入数据分布到生成数据分布的转化分布。

4. 自回归模型

5. 变分自编码器

6. 正则化流模型

7. 生成对抗网络

数学建模为随机过程，输入数据分布经历了一个过程逐步转化成最终生成图片，对转化的随机过程也考虑进去，用T步随机噪声过程来模拟（扩散模型家族）。

1.DDIM

2.SDE

3.stable diffusion

VAE

深度隐变量模型(Deep Latent Variable Models)通常长什么样子呢？

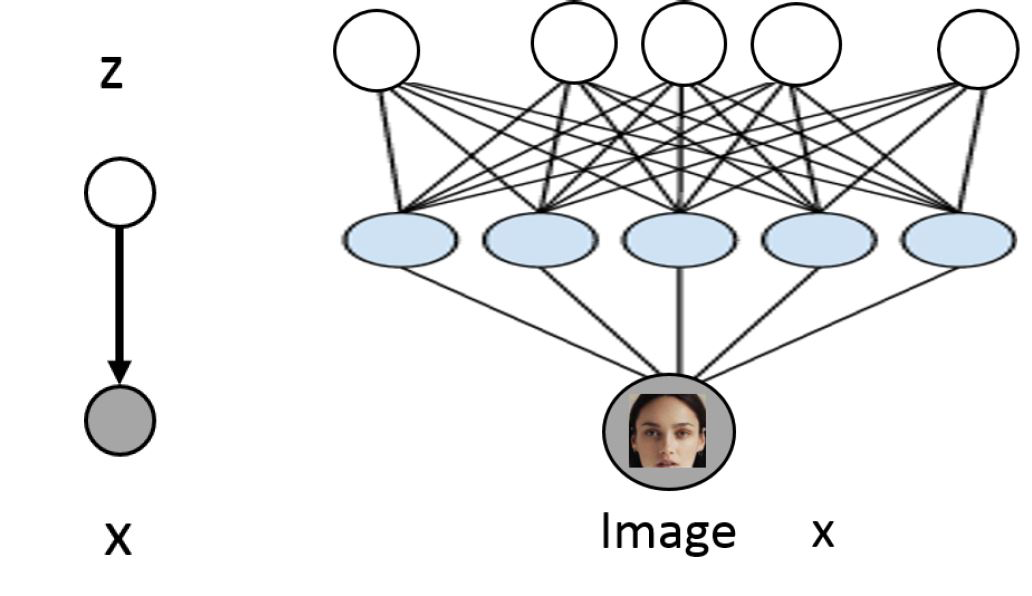
假设隐变量 z服从正态分布 z∼N(0,I)

1. p(x|z)=(μθ(z),Σθ(z)) 其中 μθ和 Σθ都是神经网络

2. 我们希望在训练完之后，z可以有一定的意义，能表示有意义的特征，这些特征可以用在无监督学习里面。

3. 特征的计算可以通过 p(z|x)

当且仅当 q=p(z|x;θ) 的时候，等号成立。证明略，读者可以带入得到，也可以参考 VI 这节的证明。

因此，我们需要找到一个分布 q(z) 它必须和 p(z|x;θ)尽可能相近的时候，才能让等式的右边的证据下界和左边的likelihood越接近。另外左边的likelihood，也被称之为evidence。

熟悉 KL divergence的读者应该已经发现，当我们把右边的式子移到左边，其实就是分布q(z)和 分布p(z|x;θ)的KL散度:

DKL(q(z)||p(z|x;θ))=logp(x;θ)−∑zq(z)logp(x,z;θ)−H(q)≥0

当然，q=p(z|x;θ)的时候，KL散度为 0。

这个时候我们就将问题转到了如何找到这样的分布 q(z)？

在开始学习VAE的参数之前，我们看看这里有两组参数需要我们优化，一组是对应于分布q 的参数 ϕ, 另一组是对应分布 p 的参数 θ，见下面的式子:

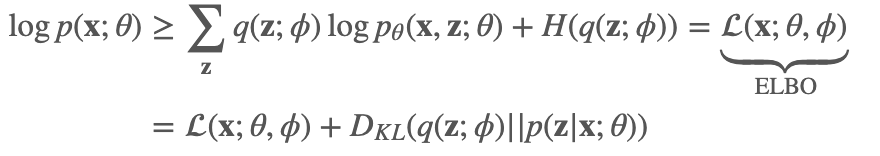
我们再来看一张学习 VAE，经常会看到的图，很好的解释了 ELBO，KL散度和likelihood之间的关系:

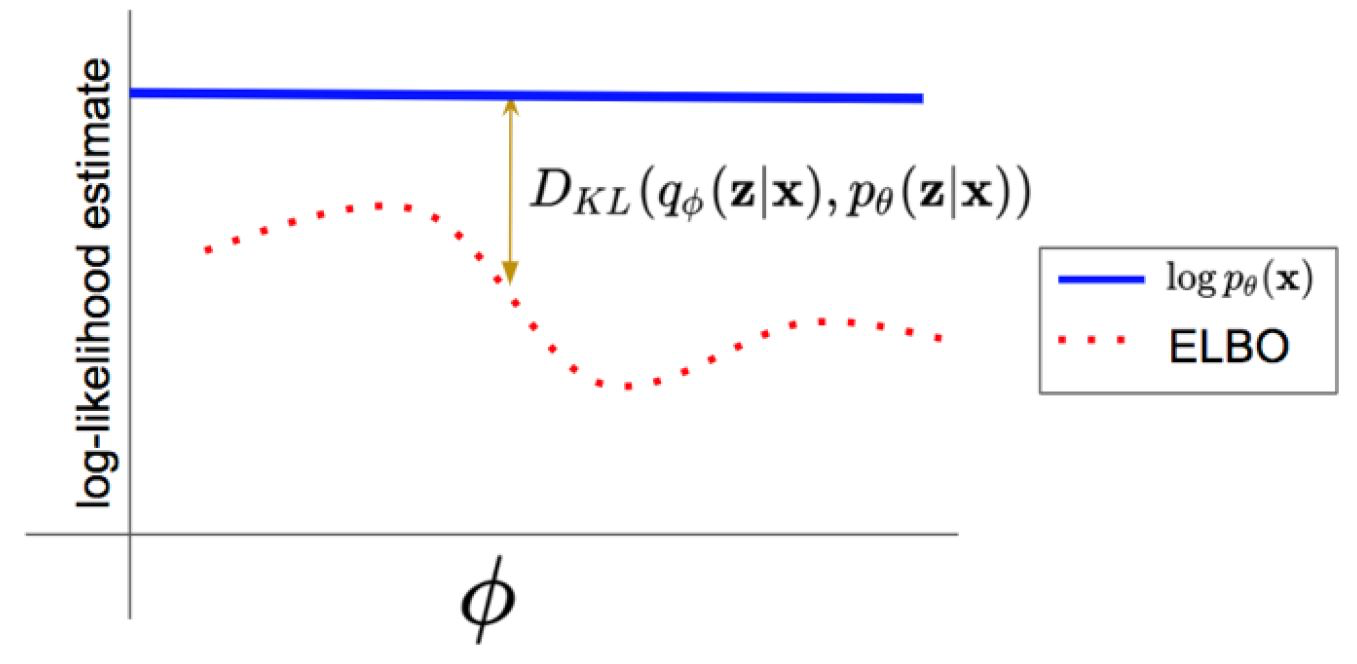
注意上面图片中的q是conditioned在x 上的，暂时可以理解为给了我们一些 x 的信息后，我们的分布 q 才能更容易接近 p(z|x;θ)，或者理解为 q的空间可以限定的小一些，这样更容易采样到有意义的样本。

从上面的推导中，我们可以看到最大化likelihood这个问题被转换为最大化证据下界ELBO。接下来，我们来看一下要怎么联合优化参数 ϕ 和 θ来最大化 ELBO。

学习Learning

根据前面的论述，我们知道我们的目标是要让证据下界尽可能的大，这里再贴一下 ELBO： 

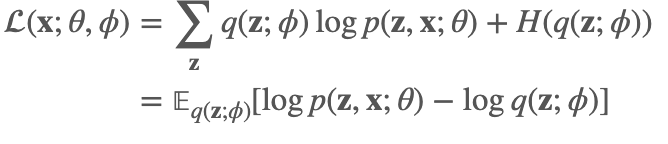
从这个式子中，我们可以看到如果我们想求 ∇θ(x;θ,ϕ)和 ∇ϕ(x;θ,ϕ)。如果这个期望函数有对应的closed-form解自然是很好的，比如我们在 VI-变分推理里举的那个例子，但是如果没有，对于前者我们求起来很方便，假设q(z;ϕ)是容易采样的，我们可以用采样的方法:

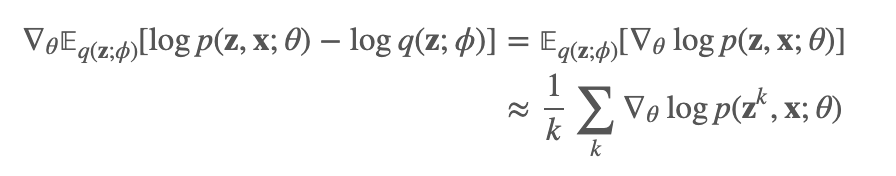
但是要怎么求 ∇ϕ(x;θ,ϕ) 呢？我们的期望是依赖 ϕ 的，这个求解过程瞬间就变复杂了，当然其实也是可以用蒙特卡洛采样的方法来求解的，这里先不讲了。我们来看看另一个方法先。

再参数化-Reparameterization

我们将上面的式子简化一下: 𝔼q(z;ϕ)[r(z)]=∫q(z;ϕ)r(z)dz

把前面ELBO方括号中的东西全部用 r(⋅) 来表示。另外需要注意其中 z 是连续随机变量。接下来假设分布 q(z;ϕ)=N(μ,σ2I), 参数为 ϕ=(μ,σ)。那么下面两种方法的采样是相同的:

1. 采样 z∼qϕ(z)

2. 采样 ϵ∼(0,I),z=μ+σϵ=g(ϵ;ϕ)

我们把第二种方法带入前面的式子: 𝔼z∼q(z;ϕ)[r(z)]=𝔼ϵ∼(0,I)[r(g(ϵ;ϕ))]=∫p(ϵ)r(μ+σϵ)dϵ

那我们再来对 ϕ�求梯度:

∇ϕ𝔼q(z;ϕ)[r(z)]=∇ϕ𝔼ϵ[r(g(ϵ;ϕ))]=𝔼ϵ[∇ϕr(g(ϵ;ϕ))]

这样我们就成功把求梯度的符号挪到了方括号里面去了，期望也不再依赖 ϕ 了。只要 r 和 g对于 ϕ 是可导的，我们就很容易用蒙特卡洛采样来计算ϕ梯度了。

𝔼ϵ[∇ϕr(g(ϵ;ϕ))]≈1k∑k∇ϕr(g(ϵk;ϕ))whereϵ1,…,ϵk∼(0,I)

我们在后面也会看到，这个trick使得我们的神经网络可以反向传导。

回到我们最初的ELBO中，我们可以看大我们的 r(z,ϕ)和这里的 r(z) 还有些差别，但是类似的，我们还是可以用reparameterization的方法将其转换为:

𝔼ϵ[∇ϕr(g(ϵ;ϕ)),ϕ]≈1k∑k∇ϕr(g(ϵk;ϕ),ϕ)whereϵ1,…,ϵk∼(0,I)

Amortized Inference

假设我们的数据样本集合为D，那么我们可以把我们的likelihood和ELBO 表达成:

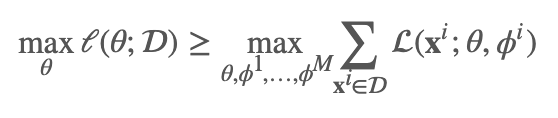
值得注意的是，我们这里每个xi 都有一个参数 ϕi与之对应，还记得我们的参数 ϕ是分布 q(z;ϕ)的参数，而这个分布是为了近似地拟合真实分布 p(z|xi;θ)，从这个真实分布中，我们都可以看到这个后验分布对于不同的数据点 𝕩i 都是不同的，因此对于不同的数据点，这个近似分布对于每个数据点的分布也应该是不同的，于是我们用不同的ϕi来表示。

但是这样一来，如果数据集很大，参数量就炸了呀。于是我们用一个参数化函数 fλ把每个 x 映射到一组变分参数上: xi→ϕi,∗。通常我们把 q(z;fλ(xi)) 写作 qϕ(z|x)。

Amortized inference: 也就是要学习怎么通过 q(z;fλ(xi))),把 xi 映射到一组好的参数上 ϕi。

于是我们的ELBO就变为: 

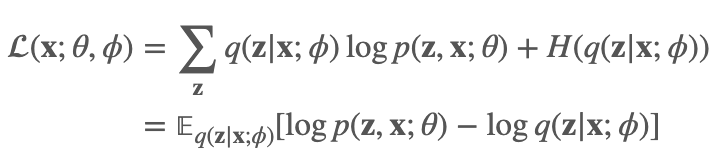
那我们的整个计算流程就是:

1. 初始化 θ(0), ϕ(0)

随机在数据集D中抽一个数据点 xi

2. 计算

3. 根据梯度方向更新θ 和 ϕ

计算梯度的方法还是用前面提到的reparameterization。

自编码器的视角

有了上面的式子之后，我们可以进一步的把上面的式子进行转换:



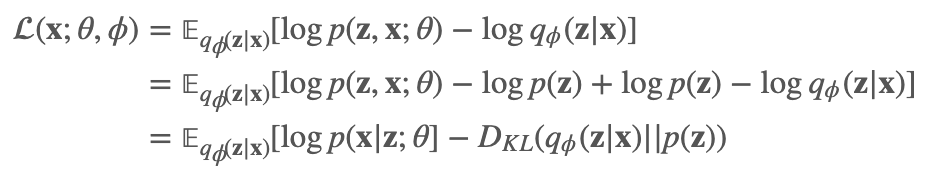
那这个式子就很有趣了。我们引入了z的先验， 我们可以把它理解为:

1. 首先，从数据集中拿出一个数据点 xi

2. 用 qϕ(z|xi)(encoder) 采样 ẑ

3. 用 p(x|ẑ ;θ) (decoder) 采样得到重建的x̂

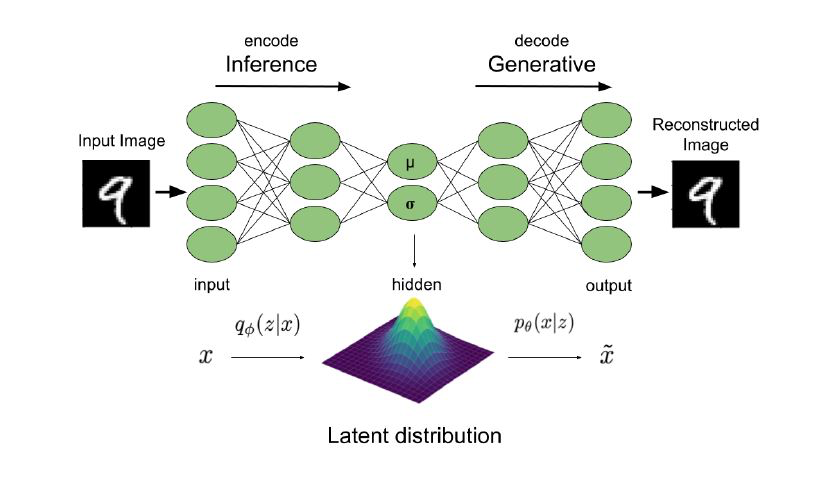
我们的训练目标 (x;θ,ϕ)，其中第一项是希望 x̂ ≈xi^，即 xi 要在 p(x|ẑ ;θ)下概率尽可能的大。第二项，是为了让 ẑ 尽可能的贴合先验 p(z)换句话说假设我们的先验是已知的，那么我们可以用它来代替qϕ直接进行采样ẑ ∼p(z)，再用解码器生成分布 p(x|ẑ ;θ)，进行采样得到样本。

GAN

一个最优的生成模型应该能够生成最好的样本质量(sample quality) 和最高的测试集的log-likelihood。但是对于不完美的模型，取得高的 log-likelihood 也许并不意味着好的样本质量，反之亦然。

Two-sample tests

给定了 S1=x∼P，S=x∼Q, 一个 two-sample test 指的是下面的两个假设(hypothesis)：

1. Null hypothesis H0:P=Q

2. Alternate hypothesis: H1:P≠Q

我们用统计指标 T 来比较 S1和 S2，比如，T 可以是两个分布均值的不同或者方差的不同。如果 T 小于一个阈值 α，那么接受 H0 否则就拒绝。我们可以看到测试统计指标 T 是 likelihood-free 的(likelihood-free)，因为它并不直接考虑计算概率密度 P或者 Q，它只比较了两个分布的样本集合S1和 S2。

先前我们假设可以直接获取到数据集S1==x∼Pdata。另外，我们有模型分布 pθ，假设模型分布允许高效率采样，S2=x∼pθ。 Alternate notion of distance between distributions (改变两个分布之间的距离定义): 训练一个生成模型从而最小化 S1 和 S2 之间的two-sample test 目标。

到这里，我们可以发现，我们把从直接在概率密度分布上建模转换到了用一个考虑两个分布上的样本的统计指标来衡量两个分布是否相同。因此找到一个好的统计指标是至关重要的，它决定了我们是否能生成出高质量的样本。

用判别器做 Two-Sample Test

在高维空间中找到这样的统计指标还是很难的，比如说两个高斯分布的方差相同，均值不同，那么它们的分布也是完全不同的。那在高维空间中更是如此，稍微某个维度有一些差异，那对应的分布可能就差很大。那么我们是不是能学习一个统计指标能找到这些差异，它最大化两个样本集S1 和 S2 之间的距离定义呢？

到这里，我们就有了两个目标，一个目标是想最小化 S1 和 S2 之间的距离，使得 S2 的样本尽量逼近 S1；另一个目标是最大化 S1和 S2 样本之间的距离，找到那些会让两个分布很不相同的差异。

生成对抗网络

生成对抗网络是两个玩家之间的零和游戏，这两个玩家是 生成器 和 判别器。

生成器 (generator) 是一个有向的隐变量模型，隐变量 z和生成样本x之间的映射为 Gθ。它的目标为最小化 two-sample test。

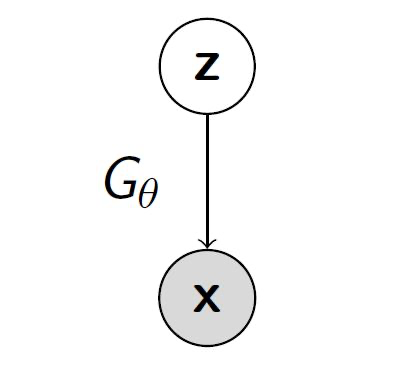
判别器 (discriminator) 是一个函数比如神经网络，用来区分来自数据集的”真实”数据，和来自模型生成器的”伪造”数据。它的目标为最大化 two-sample test。

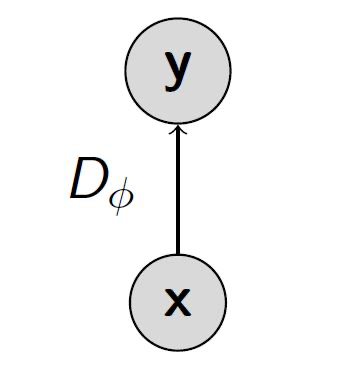
训练目标

判别器的训练目标为:

上面的式子可以理解为，对于一个固定的生成器，判别器就是做了一个二分类，交叉熵为目标，当x∼pdata，即样本来自真实数据集，那么概率赋值为1，当 x∼pG，即样本来自生成器，那么概率赋值为0.

最优的判别器有:

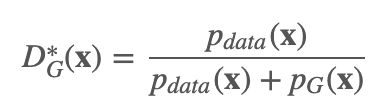
证明：对于给定的生成器 G，判别器 D 的训练目标就是要最大化 V(G,D)

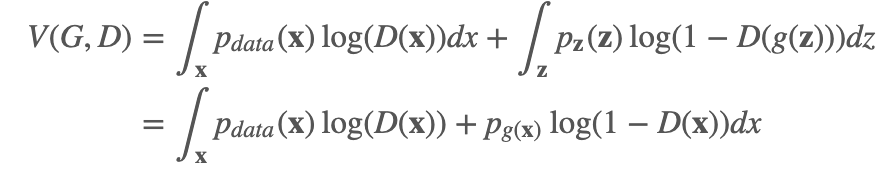
对于任意的 (a,b)∈R2,(a,b)≠0,0(，函数 y→alog(y)+blog(1−y)，在区间 [0,1][0,1] 上的取得最大值的地方在 aa+b。因此，令y=D(x)，即可得证。

对于生成器，我们的训练目标为:

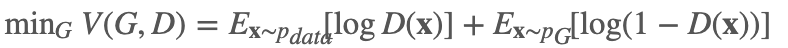
也就是说我们希望能找到一个生成器，使得判别器的目标不能实现(最小)，因此也就产生了对抗。

这时，将最优判别器 D∗G(⋅) 带入，我们有:

DJSD 表示为 2xJensen-Shannon Divergence，也叫做对称KL散度，写作:

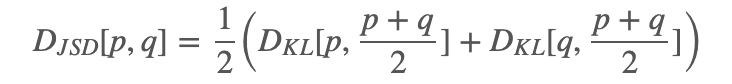
训练流程

我们来总结一下 GAN 的训练步骤:

从真实数据D中采样 m个训练样本 x(1),x(2),…,x(m)

1. 从噪声分布 pz 中采样 m 个噪声向量 z(1),z(2),…,z(m)

2. 用随机梯度下降更新生成器参数 θ

因为我们这里是更新生成器，所以不关注 V的第一项(从真实数据采样)。

3. 用随机梯度上升更新判别器参数 ϕ

4. 以上步骤重复固定个epochs

上面的训练过程是先训练生成器然后训练判别器，这个顺序也可以反过来。

训练 GAN 中带来的困难

GAN的训练是比较困难的，许多论文提出了很多的tricks，主要的困难有以下几个方面:

1. 不稳定的优化过程 Unstable optimization

2. Mode collapse

3. 评估 Evaluation

Unstable optimization

理论上来说，在每个step，判别器如果达到了最优，生成器在函数空间中更新，那么生成器是能够收敛到数据分布的。但是实际训练过程中，生成器和判别的损失函数值总是震荡着的。也不同于极大似然估计MLE，应该什么时候停止训练也很难判断。

Mode Collapse

Mode Collapse 主要指的是GAN的生成器总是只生成固定的一个或几个样本，类似于modes(众数)。事实上，笔者发现其它的一些生成模型也会有这个问题。

课件中给的例子是这样的：假设我们的真实分布是混合高斯(mixture of Gaussians)

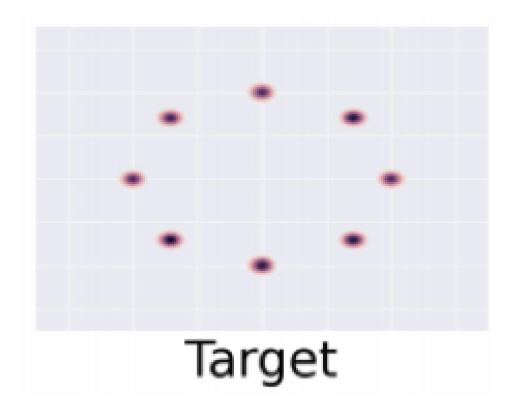
但是在生成过程中，我们的生成器分布总是在各个中心点之间跳来跳去。

对于众数问题，可以通过改变架构，增加正则项，引入噪音干扰等方法。这里有个repo，给了许多GAN的训练建议和tricks。

FLOW

自回归模型虽然似然likelihood很容易计算但是没有直接的办法来学习特征。 变分自编码器虽然可以学习特征的表示(隐变量 z 但是它的边缘似然函数很难求，所以我们取而代之用了最大化证据下界ELBO来近似求解。

我们有没有办法设计一个含有隐变量的模型并且它的似然函数也容易求呢？的确是有的。 我们对这样的模型还有些其他要求，除了概率密度是可以计算的，还需要容易采样。许多简单的分布像是高斯和均匀分布都是满足这个要求的。但是实际的数据分布是很复杂的。那有什么办法可以用这些容易采样又容易计算概率密度的分布映射到复杂分布呢？有的，用换元法(change of variables)

在后面的部分中，读者可以记住 z 来自于一个容易采样的分布，x 来自于实际的数据的复杂分布。

在介绍 Flow 模型前，我们先来看一些基本概念。

换元法

相信大家对这个概念都不陌生。如果读者对这个概念不熟悉，可以参考这个网站。

先来贴一下一维的公式: 如果 X=f(Z)，f(⋅) 是单调的并且它的逆函数 Z=f−1(X)=h(X)，那么:

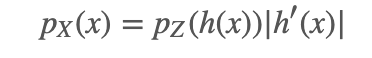
举个例子，假设 Z=1/4X并且 Z∼[0,2], 那么 pX(4)为多少? 带入公式 h(X)=X/4ℎ，所以 pX(4)=pZ(1)h′(4)=1/2×1/4=1/8。

更一般的，假设 Z 是一个均匀随机向量 [0,1]^n，X=AZ，其中 A 是一个可逆的方阵，它的逆矩阵为 W=A−1，那么 X 是怎么分布的？

矩阵 A 是把一个单位超立方体 [0,1]n 变成了一个超平行体。超立方体和超平行四边形是正方形和平行四边形的更一般式。下图中，我们看到这里的变换矩阵

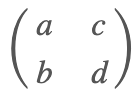
把单位正方形变成了一个任意的平行四边形。

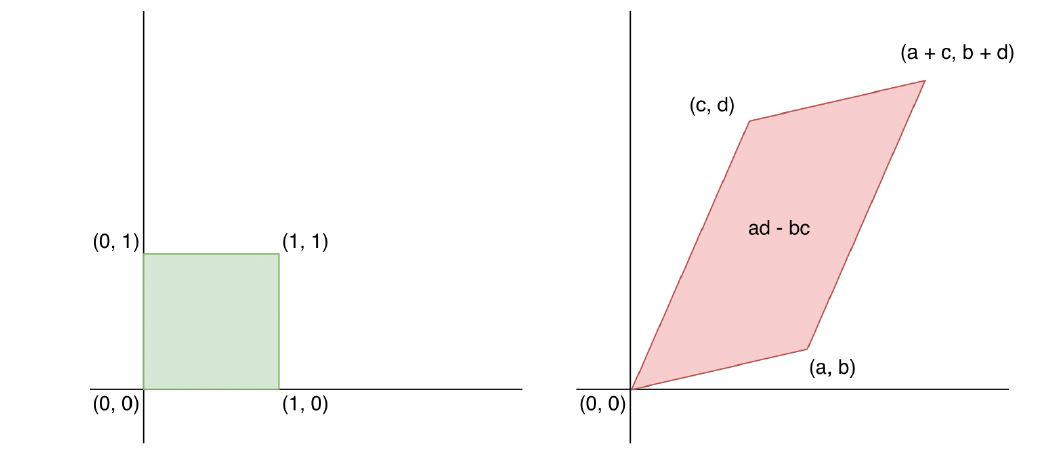
超平行四边形体的体积(volume) 等于转换矩阵 A的行列式的值。

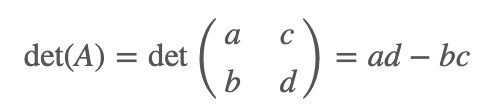
因为 X是均匀分布在超四边形上的，因此:

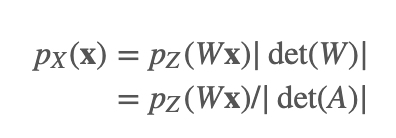
标准化流模型 Normalizing Flow Models

在一个标准流模型(normalizing flow model)， 假设 Z和 X分别为隐变量和观测变量，并且他们之间的映射为函数 f:ℝn↦ℝn，并且它是可逆的，那么 X=f(Z)，Z=f−1(X):

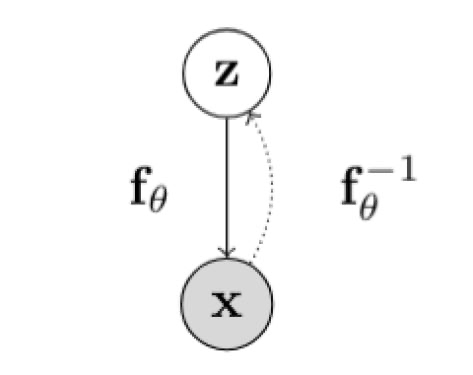
那么利用换元法，可以得到观测变量的似然值为:

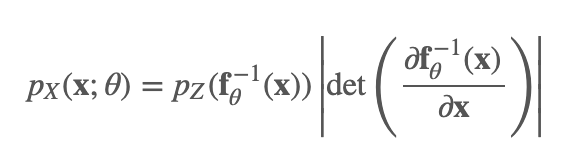
这里的 f 转换函数我们加上了参数下标 θ，也就是我们的神经网络学习的参数。从这个公式中，我们可以看到，假设我们的隐变量来自一个简单分布，我们经过转换 fθ，可以把它隐射到复杂分布 pX上，并且当我们想要计算观测变量的概率值的时候只需要把这个过程逆转过来，用 f−1对 x 进行转换并代入到简单分布pZ中，乘以相应的行列式的值即可。当然，读者应该会有疑惑，如何保证这个转换是可逆的呢？这个我们后面再提。

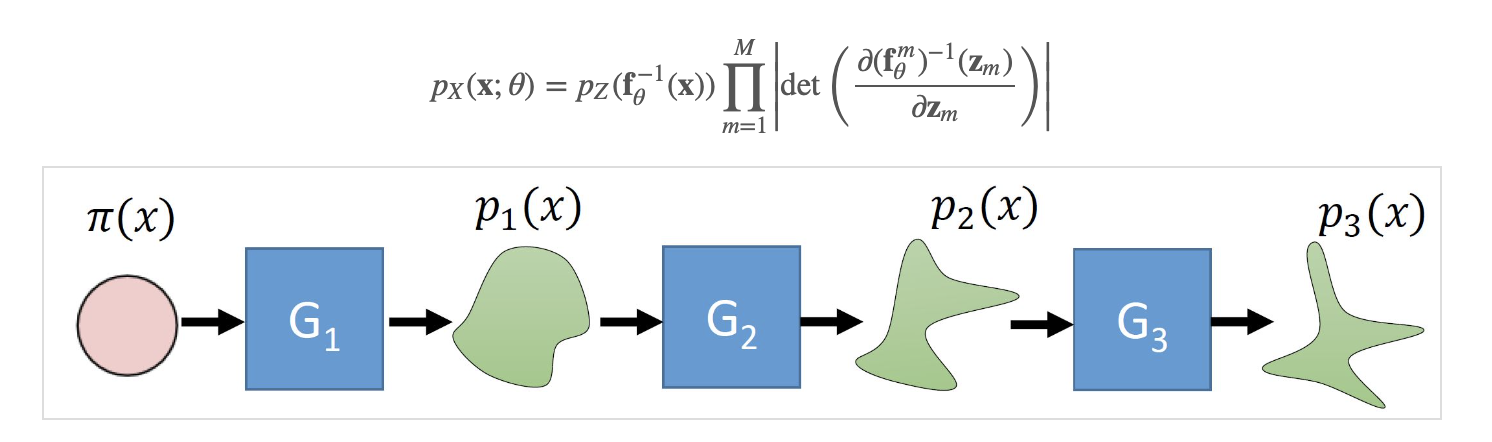
这里插一张笔者从李宏毅老师的课件里摘来的图:

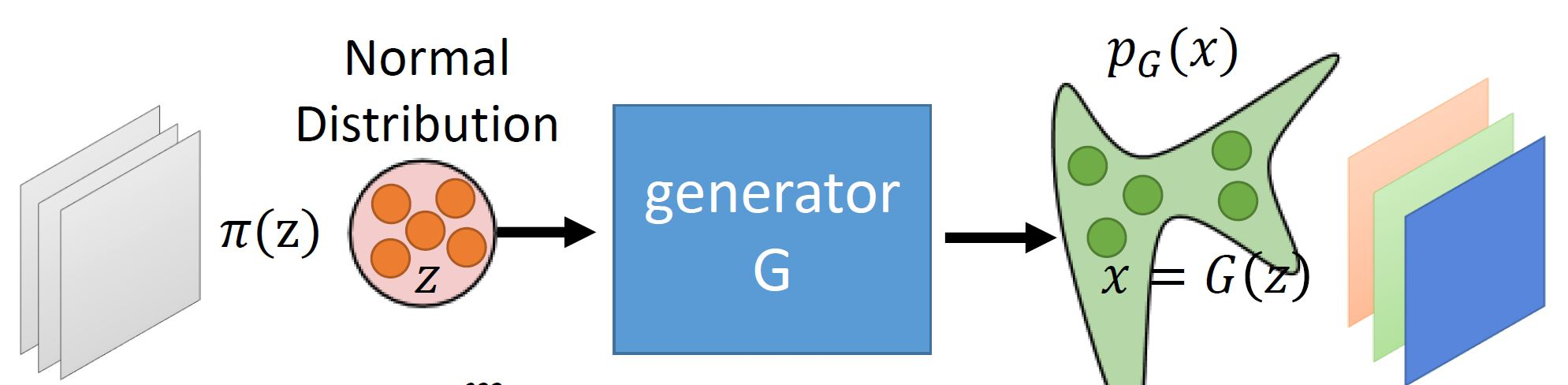
这里的generator，也就是我们的 fθ，这里的正太分布π(z) 即为简单分布 pZ。

流式转换(flow of transformations)

标准化-Normalizing 换元法使得我们用一个可逆变换得到了标准化的概率密度。那么 流-Flow 的意思指的是一系列的可逆变换互相组合在一起:

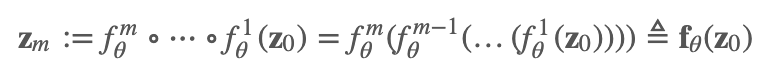
1. 首先 z0 来自于一个简单分布，例如，高斯分布

2. 用 M 个可逆转换后得到了 x，即: x≜zM

3. 通过换元，我们可以得到 (乘积的行列式等于行列式的乘积):

Planar flows

Planar flow 指的flow模型是它的可逆转换为:

具体的代码，可以参考这个repo，但是这里的代码中的分布是由close-form解的，loss其实用的是KL divergence，和我们所希望学习的任意的实际数据分布(没有close-formed)是不一样的，之所以不能学习任意分布是因为论文中也没给出计算Likelihoode所需要的 f−1，论文参考这里。 后面我们会写要怎么设计这个转换。

下图是 Planar flow 通过多次转换后把简单的高斯分布变成了复杂的一个分布:

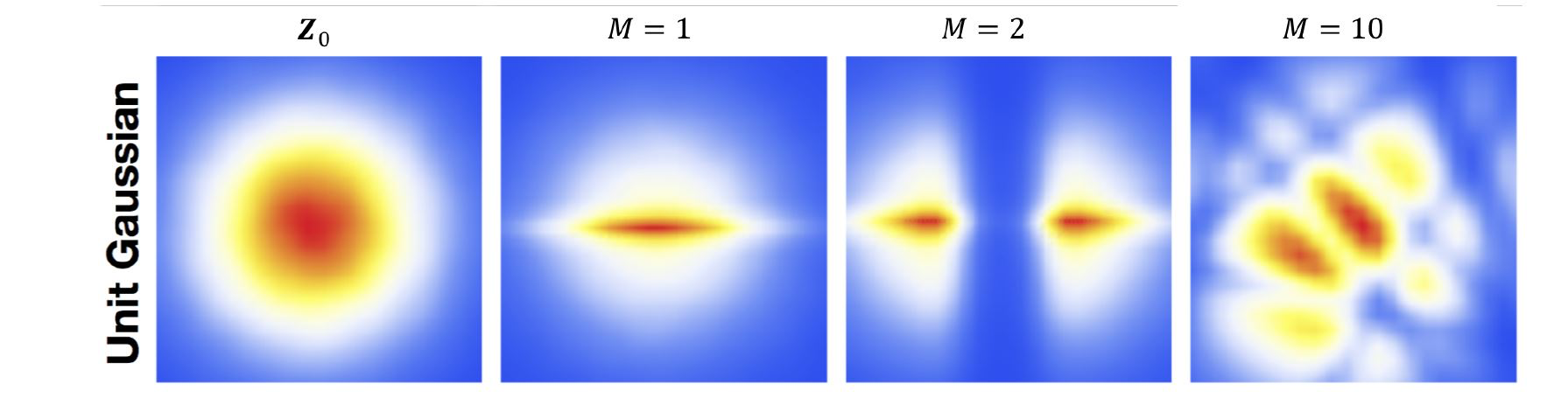
学习和推理

我们把上面的likelhood，加上log，得到在数据集D上的极大似然为:

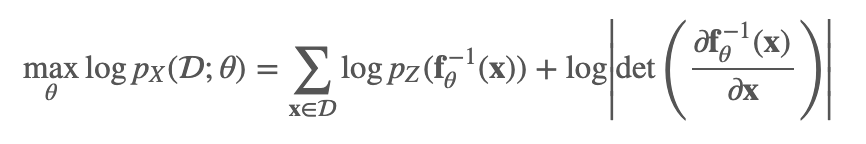
当我们训练完模型，想要采样的时候，可以通过前向转换 z↦x z∼pZ(z)x=fθ(z)

学习隐变量的表示可以通过逆转换得到，比如我们有一张图片，我们可以得到它的特征:

z=f−1θ(x)

因为计算Jacobian的行列式值复杂度很高 O(n3)，但是我们知道上三角/下三角矩阵的行列式的值为对角线元素相乘 O(n)，所以复杂度一下子就降下来了。所以我们可以按照这个思路来设计我们的可逆转换函数。

NICE

NICE(Non-linear Independent Components Estimation)，源自这里。它包含了两种类型的层，additive coupling layers 和 rescaling layers。

Additive coupling layers

首先我们把隐变量 z 分成两个部分z1:d 和 zd+1:n，1≤d<n1。

那么我们的前向映射: z↦x

1. x1:d=z1:d (直接拷贝过去)

2. xd+1:n=zd+1:n+mθ(z1:d)，其中mθ(⋅)是一个神经网络，参数为 θ，输入为维度为 d，输出维度为 n−d。

逆映射:x↦z

3. z1:d=x1:d (直接拷贝回去）

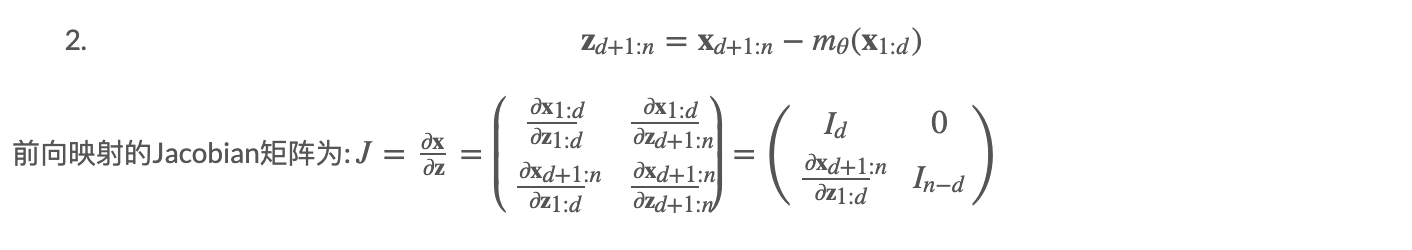
因此，det(J)=1det(下三角矩阵，且对角线为1)，当行列式的值为1的时候，我们称这种变换为 Volume preserving transformation。

这些 coupling layers 可以任意叠加下去，所以是 additive的。并且每一层的隐变量分隔partition可以是不一样的(d 的取值每一层都可以不同)。

Rescaling layers

NICE 的最后一层用了一个 rescaling transformation。同样地，

前向映射: z↦x: xi=sizi

其中, si 是第i维的scaling factor.

逆映射:x↦z:

zi=xisi

前向映射的Jacobian矩阵为:

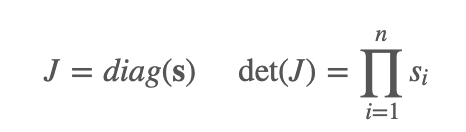
好了，我们的每种类型的曾都有前向映射和逆映射了，就可以开开心心的训练我们的神经网络了。

Real-NVP

Real-NVP(Non-volume presreving extention of NICE)是NICE模型的一个拓展，可以参考这篇论文。

如下图所示:

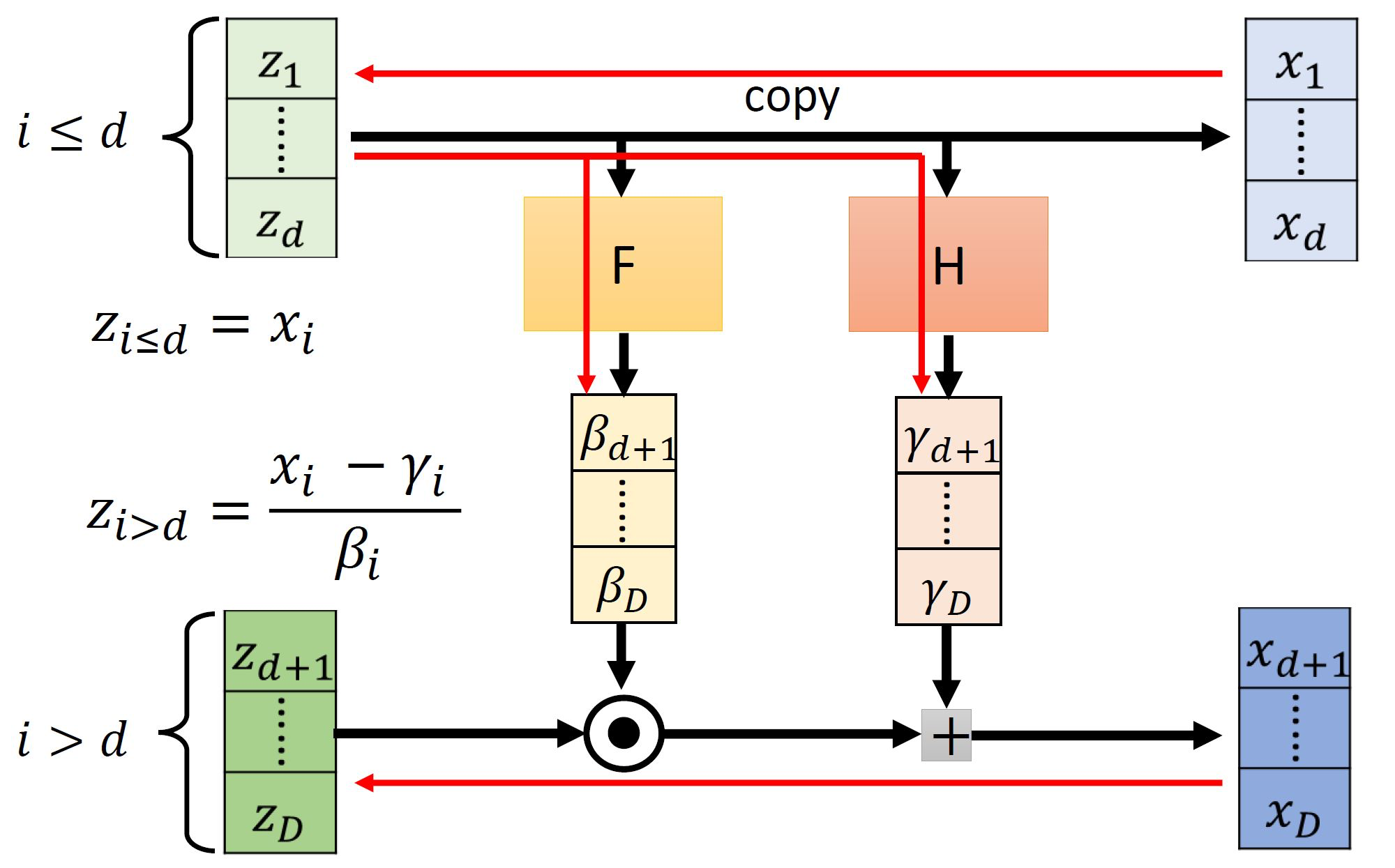
我们可以发现 z1:d 基本都是直接复制下去了，其实也可以让 z1:d和 zd+1:n 反一下，如下图(叠加了3个coupling layers):

将自回归模型看成流模型

这一节中，我们尝试理解如何把自回归模型看成是流模型，接着我们介绍两种模型Masked Autoregressive Flow (MAF) 和 Inverse Autoregressive Flow (IAF)模型。

假设我们的自回归模型:

MAF

我们的MAF(Masked Autoregressive Flow)的前向映射:

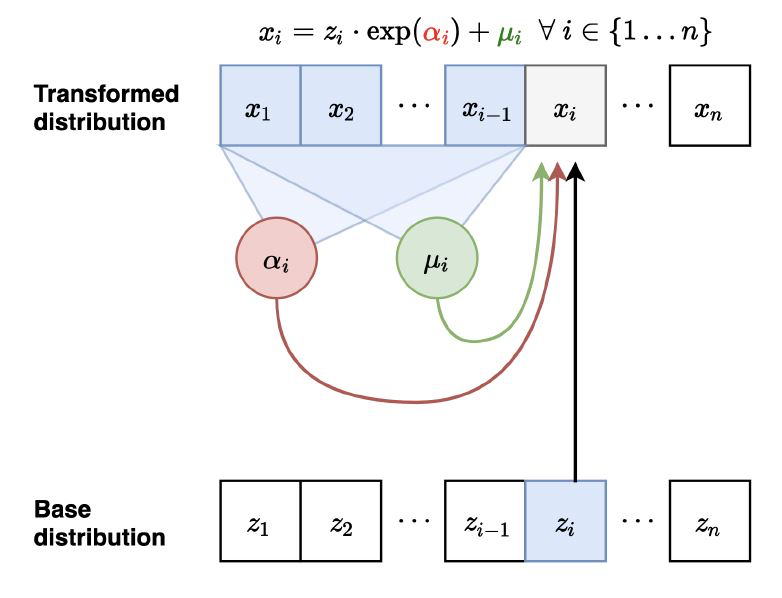
那么它的前向映射: z↦x

1. 让 x1=exp(α1)z1+μ1。并且计算 μ2(x1),α2(x1)

2. 让 x2=exp(α2)z2+μ2。并且计算 μ3(x1,x2),α3(x1,x2)

采样依然是序列化的并且慢(和自回归一样)，需要 O(n) 的时间。

逆映射如下图:

逆映射:x↦z

3. 所有的 μi和 αi 都可以并行计算，因为 zi 互相没有依赖关系。比如我们可以用自回归文章中介绍的 MADE 模型来做。

4. z1=(x1−μ1)/exp(α1)

5. z2=(x2−μ2)/exp(α2)

6. …

Jacobian矩阵是下三角，因此行列式的值计算起来也很快。 似然值评估(likelihood estimation)起来也很简单方便，并且是并行的。(因为zi可以并行计算)

IAF

前面的MAF，我们发现采样是很慢的但是计算likelihood很快，而在IAF(Inverse Autoregressive Flow)中这种情况反了过来。同样地，我们分别来看看前向映射，逆映射和Jacobian值。

前向映射: z↦x (并行)：

1. 对 i=1,…,n 采样 zi∼(0,1)

2. 并行计算好所有的 μi 和 αi

3. x1=exp(α1)z1+μ1

4. x2=exp(α2)z2+μ2

逆映射:x↦z (序列化计算):

5. 让 z1=(x1−μ1)/exp(α1), 根据 z1计算μ2(z1), α2(z1)

6. 让 z2=(x2−μ2)/exp(α2), 根据 z1,z2 计算 μ3(z1,z2),α3(z1,z2)

从上面的映射中可以看到采样很方便， 计算数据点的likelihood很慢(训练)。

注意，IAF对给定的数据点x计算likelihood慢，但是评估计算它自己生成的点的概率是很快的。

IAF 是 MAF 的逆过程

如下图，我们发现在 MAF 的逆转换中，把 x 和 z交换一下，就变成了 IAF 的前向转换。类似地。 MAF 的前向转换是 IAF的逆转换。

MAF的likelihood计算很快，采样很慢。IAF的采样很快，likelihood计算很慢。所以MAF更适合基于极大似然估计(MLE)的训练过程以及概率密度计算，IAF更适合实施的生成过程。那我们可以同时利用两个模型的优点吗？

Parallel Wavenet

接下来就看一下我们怎么同时利用 MAF 和 IAF 的特点，训练一个采样和训练都很快的模型。

Parallel Wavenet 分两个部分，一个老师模型，一个学生模型。 其中老师模型是 MAF， 用来做训练计算极大似然估计MLE。 一旦老师模型训练好了之后，我们再来训练学生模型。学生模型用 IAF，虽然学生模型不能快速计算给定的外部数据点的概率密度，但是它可以很快地采样，并且它也可以直接计算它的隐变量的概率密度。

概率密度蒸馏(Probability density distillation): 学生模型的训练目标是最小化学生分布 s和 老师分布 t�之间的 KL 散度。

DKL(s,t)=Ex∼s[logs(x)−logt(x)]

计算流程为:

1. 用学生模型 IAF 抽取样本 x (详见IAF前向转换)

2. 获得学生模型的概率密度 (这里的概率密度直接用上一步中的z和相应的Jacobian矩阵的值exp(∑ni=1αi)得到)

3. 用老师模型 MAF 计算，根据学生模型采样得到的 x样本的概率密度。

4. 计算KL散度

整体的训练过程就是:

5. 用极大似然训练老师模型 MAF

6. 用最小化和老师模型的分布的KL散度训练学生模型 IAF

测试过程: 用学生模型直接测试，生成样本

这个流程的效率比原来的 Wavenet-自回归模型快了近1000倍!

Parallel Wavenet 论文

我们来看一下这个模型的图:

首先呢，我们的老师模型 MAF 已经是训练好了，注意在训练过程中会加上一些语言学信息特征 linguistic features(通常大家用的都是spectrogram频谱，笔者不是很确定直接加像是文字特征行不行)。接着呢，我们让学生模型 IAF 进行采样，采样得到的样本(紫色的圈圈)放到老师模型中去评估概率密度。

WaveGlow

我们还是回到Glow模型来看看另一个例子，WaveGlow

这里的 WN 模块指的是类似于WaveNet中的结构，实际上它可以是任意的神经网络结构，作者用了膨胀卷积(dilated convolutions)和gated-tanh，invertible 1x1 convolution可以参考这篇论文。稍微注意一下，我们前面都是从 z↦x，现在这张图我们是直接看的逆转换x↦z(毕竟在训练的时候，我们就是在用 z 计算likelihood)。

代码可以参考这里。

diffusion发展史

对于扩散模型技术正在蓬勃发展期，网上的资料也很多很全面，各种综述文章也不少。我就不在做更多阐述，会把一些我觉得整理不错的技术帖综合放进文章，减少大家文章检索的工作保持阅读流畅。

其实diffusion模型和上面一些模型的主要差异在于对生成过程的建模。相当于是通过增加了一个随机生成过程的仿真让生成内容质量可控。

扩散模型（diffusion models）是深度生成模型中新的SOTA。扩散模型在图片生成任务中超越了原SOTA：GAN，并且在诸多应用领域都有出色的表现，如计算机视觉，NLP、波形信号处理、多模态建模、分子图建模、时间序列建模、对抗性净化等。此外，扩散模型与其他研究领域有着密切的联系，如稳健学习、表示学习、强化学习。然而，原始的扩散模型也有缺点，它的采样速度慢，通常需要数千个评估步骤才能抽取一个样本；它的最大似然估计无法和基于似然的模型相比；它泛化到各种数据类型的能力较差。如今很多研究已经从实际应用的角度解决上述限制做出了许多努力，或从理论角度对模型能力进行了分析。

然而，现在缺乏对扩散模型从算法到应用的最新进展的系统回顾。为了反映这一快速发展领域的进展，我们对扩散模型进行了首个全面综述。我们设想我们的工作将阐明扩散模型的设计考虑和先进方法，展示其在不同领域的应用，并指出未来的研究方向。此综述的概要如下图所示：

尽管diffusion model在各类任务中都有着优秀的表现，它仍还有自己的缺点，并有诸多研究对diffusion model进行了改善。为了系统地阐明diffusion model的研究进展，我们总结了原始扩散模型的三个主要缺点，采样速度慢，最大化似然差、数据泛化能力弱，并提出将的diffusion models改进研究分为对应的三类：采样速度提升、最大似然增强和数据泛化增强。我们首先说明改善的动机，再根据方法的特性将每个改进方向的研究进一步细化分类，从而清楚的展现方法之间的联系与区别。在此我们仅选取部分重要方法为例， 我们的工作中对每类方法都做了详细的介绍，内容如图所示：

在分析完三类扩散模型后，我们将介绍其他的五种生成模型GAN，VAE，Autoregressive model, Normalizing flow, Energy-based model。考虑到扩散模型的优良性质，研究者们已经根据其特性将diffusion model与其他生成模型结合，所以为了进一步展现diffusion model 的特点和改进工作，我们详细地介绍了diffusion model和其他生成模型的结合的工作并阐明了在原始生成模型上的改进之处。Diffusion model在诸多领域都有着优异的表现，并且考虑到不同领域的应用中diffusion model产生了不同的变形，我们系统地介绍了diffusion model的应用研究，其中包含如下领域：计算机视觉，NLP、波形信号处理、多模态建模、分子图建模、时间序列建模、对抗性净化。对于每个任务，我们定义了该任务并介绍利用扩散模型处理任务的工作，我们将本项工作的主要贡献总结如下：

l 新的分类方法：我们对扩散模型和其应用提出了一种新的、系统的分类法。具体的我们将模型分为三类：采样速度提升、最大似然提升、数据泛化提升。进一步地，我们将扩散模型的应用分为七类：计算机视觉，NLP、波形信号处理、多模态建模、分子图建模、时间序列建模、对抗性净化。

l 全面的回顾：我们首次全面地概述了现代扩散模型及其应用。我们展示了每种扩散模型的主要改进，和原始模型进行了必要的比较，并总结了相应的论文。对于扩散模型的每种类型的应用，我们展示了扩散模型要解决的主要问题，并说明它们如何解决这些问题

l 未来研究方向：我们对未来研究提出了开放型问题，并对扩散模型在算法和应用方面的未来发展提供了一些建议。

二． 扩散模型基础

生成式建模的一个核心问题是模型的灵活性和可计算性之间的权衡。扩散模型的基本思想是正向扩散过程来系统地扰动数据中的分布，然后通过学习反向扩散过程恢复数据的分布，这样就了产生一个高度灵活且易于计算的生成模型。

A. Denoising Diffusion Probabilistic Models（DDPM）

一个DDPM由两个参数化马尔可夫链组成，并使用变分推断以在有限时间后生成与原始数据分布一致的样本。前向链的作用是扰动数据，它根据预先设计的噪声进度向数据逐渐加入高斯噪声，直到数据的分布趋于先验分布，即标准高斯分布。反向链从给定的先验开始并使用参数化的高斯转换核，学习逐步恢复原数据分布。用 x0 ~q(x0) 表示原始数据及其分布,则前向链的分布是可由下式表达：

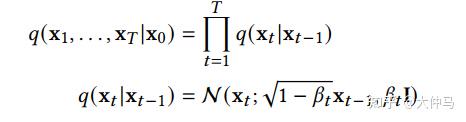
这说明前向链是马尔可夫过程， xt 是加入t步噪音后的样本， βt 是事先给定的控制噪声进度的参数。当 ∏t1−βt趋于1时， xT 可以近似认为服从标准高斯分布。当 βt 很小时，逆向过程的转移核可以近似认为也是高斯的：

我们可以将变分下界作为损失函数进行学习：

B. Score-Based Generative Models（SGM）

上述DDPM可以视作SGM的离散形式。SGM构造一个随机微分方程（SDE）来平滑的扰乱数据分布，将原始数据分布转化到已知的先验分布：

和一个相应的逆向SDE，来将先验分布变换回原始数据分布：

因此，要逆转扩散过程并生成数据，我们需要的唯一信息就是在每个时间点的分数函数。利用score-matching的技巧我们可以通过如下损失函数来学习分数函数：

对两种方法的进一步介绍和两者关系的介绍请参见我们的文章。

原始扩散模型的三个主要缺点，采样速度慢，最大化似然差、数据泛化能力弱。最近许多研究都在解决这些缺点，因此我们将改进的扩散模型分为三类：采样速度提升、最大似然增强和数据泛化增强。在接下来的三、四、五节我们将对这三类模型进行详细的介绍。

三． 采样加速方法

在应用时，为了让新样本的质量达到最佳，扩散模型往往需要进行成千上万步计算来获取一个新样本。这限制了diffusion model的实际应用价值，因为在实际应用时，我们往往需要产生大量的新样本，来为下一步处理提供材料。研究者们在提高diffusion model采样速度上进行了大量的研究。我们对这些研究进行了详细的阐述。我们将其细化分类为三种方法：Discretization Optimization，Non-Markovian Process，Partial Sampling。

A. Discretization Optimization方法优化求解diffusion SDE的方法。因为现实中求解复杂SDE只能使用离散解来逼近真正的解，所以该类方法试图优化SDE的离散化方法，在保证样本质量的同时减少离散步数。SGM 提出了一个通用的方法来求解逆向过程，即对前向和后向过程采取相同的离散方法。如果给定了前向SDE的离散方式：

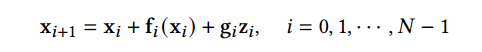
那么我们就可以以相同的方式离散化逆向SDE：

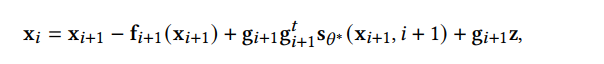
这种方法比朴素DDPM效果略好一点。进一步，SGM向SDE求解器中加入了一个矫正器，从而让每一步生成的样本都有正确的分布。在求解的每一步，求解器给出一个样本后，矫正器都使用马尔可夫链蒙特卡罗方法来矫正刚生成的样本的分布。实验表明向求解器中加入矫正器比直接增加求解器的步数效率更高。

B. Non-Markovian Process方法突破了原有Markovian Process的限制，其逆过程的每一步可以依赖更多以往的样本来进行预测新样本，所以在步长较大时也能做出较好的预测，从而加速采样过程。其中主要的工作DDIM，不再假设前向过程是马尔可夫过程，而是服从如下分布：

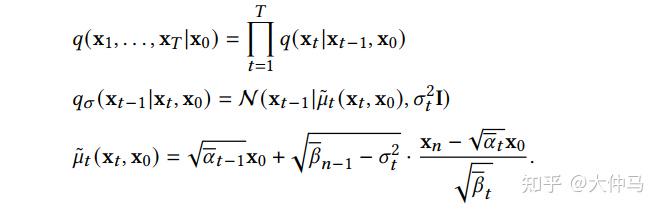
DDIM的采样过程可以视为离散化的神经常微分方程，其采样过程更高效，并且支持样本的内插。进一步的研究发现DDIM可以视作流形上扩散模型PNDM的特例。

C. Partial Sampling方法通过在generation process中忽略一部分的时间节点，而只使用剩下的时间节点来生成样本，直接减少了采样时间。例如，Progressive Distillation从训练好的扩散模型中蒸馏出效率更高的扩散模型。对于训练好的一个扩散模型，Progressive Distillation会从新训练一个扩散模型，使新的扩散模型的一步对应于训练好的扩散模型的两步，这样新模型就可以省去老模型一半的采样过程。具体算法如下：

不断循环这个蒸馏过程就能让采样步骤指数级下降。

四． 最大似然估计加强

扩散模型在最大似然估计的表现差于基于似然函数的生成模型，但最大化似然估计在诸多应用场景都有重要意义，比如图片压缩, 半监督学习, 对抗性净化。由于对数似然难以直接计算，研究主要集中在优化和分析变分下界（VLB）。我们对提高扩散模型最大似然估计的模型进行了详细的阐述。我们将其细化分类为三类方法：Objectives Designing，Noise Schedule Optimization，Learnable Reverse Variance。

A. Objectives Designing方法利用扩散 SDE推倒出生成数据的对数似然与分数函数匹配的损失函数的关系。这样通过适当设计损失函数，就可以最大化 VLB 和对数似然。 Song et al. 证明了可以设计损失函数的权重函数，使得plug-in reverse SDE 生成样本的似然函数值小于等于损失函数值，即损失函数是似然函数的上界。分数函数拟合的损失函数如下：

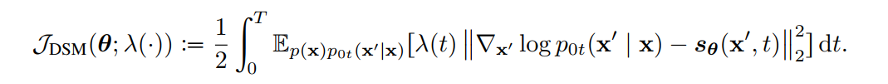
我们只需将权重函数 λ(t) 设为扩散系数g（t）即可让损失函数成为似然函数的VLB，即：

B. Noise Schedule Optimization通过设计或学习前向过程的噪声进度来增大VLB。VDM证明了当离散步数接近无穷时，损失函数完全由信噪比函数SNR（t）的端点决定：

那么在离散步数接近无穷时，可以通过学习信噪比函数SNR（t）的端点最优化VLB，而通过学习信噪比函数中间部分的函数值来实现模型其他方面的改进。

C. Learnable Reverse Variance方法学习反向过程的方差，从而较少拟合误差，可以有效地最大化VLB。Analytic-DPM证明，在DDPM和DDIM中存在反向过程中的最优期望和方差：

使用上述公式和训练好的分数函数，在给定前向过程的条件下，最优的VLB可以近似达到。

五． 数据泛化增强

扩散模型假设数据存在于欧几里得空间，即具有平面几何形状的流形，并添加高斯噪声将不可避免地将数据转换为连续状态空间，所以扩散模型最初只能处理图片等连续性数据，直接应用离散数据或其他数据类型的效果较差。这限制了扩散模型的应用场景。数个研究工作将扩散模型推广到适用于其他数据类型的模型，我们对这些方法进行了详细地阐释。我们将其细化分类为两类方法：Feature Space Unification，Data-Dependent Transition Kernels。

A. Feature Space Unification方法将数据转化到统一形式的latent space，然后再latent space上进行扩散。LSGM提出将数据通过VAE框架先转换到连续的latent space 上后再在其上进行扩散。这个方法的难点在于如何同时训练VAE和扩散模型。LSGM表明由于潜在先验是intractable的，分数匹配损失不再适用。LSGM直接使用VAE中传统的损失函数ELBO作为损失函数，并导出了ELBO和分数匹配的关系：

该式在忽略常数的意义下成立。通过参数化扩散过程中样本的分数函数，LSGM可以高效的学习和优化ELBO。

B. Data-Dependent Transition Kernels方法根据数据类型的特点设计diffusion process 中的transition kernels，使扩散模型可以直接应用于特定的数据类型。D3PM为离散型数据设计了transition kernel，可以设为lazy random-walk，absorbing state等。GEODIFF为3D分子图数据设计了平移-旋转不变的图神经网络，并且证明了具有不变性的初分布和transition kernel可以导出具有不变性的边缘分布。假设T是一个平移-旋转变换，如：

那么生成的样本分布也有平移-旋转不变性：

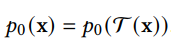
六． 和其他生成模型的联系

在下面的每个小节中，我们首先介绍其他五类重要的生成模型，并分析它们的优势和

局限性。然后我们介绍了扩散模型是如何与它们联系起来的，并说明通过结合扩散模型来改进这些生成模型。VAE，GAN，Autoregressive model, Normalizing flow, Energy-based model和扩散模型的联系如下图所示：

A. DDPM可以视作层次马尔可夫VAE（hierarchical Markovian VAE）。但DDPM和一般的VAE也有区别。DDPM作为VAE，它的encoder和decoder都服从高斯分布、有马尔科夫行；其隐变量的维数和数据维数相同；decoder的所有层都共用一个神经网络。

B. DDPM可以帮助GAN解决训练不稳定的问题。因为数据是在高维空间中的低维流形中，所以GAN生成数据的分布和真实数据的分布重合度低，导致训练不稳定。扩散模型提供了一个系统地增加噪音的过程，通过扩散模型向生成的数据和真实数据添加噪音，然后将加入噪音的数据送入判别器，这样可以高效地解决GAN无法训练、训练不稳定的问题。

C. Normalizing flow通过双射函数将数据转换到先验分布，这样的作法限制了Normalizing flow的表达能力，导致应用效果较差。类比扩散模型向encoder中加入噪声，可以增加Normalizing flow的表达能力，而从另一个视角看，这样的做法是将扩散模型推广到前向过程也可学习的模型。

D. Autoregressive model在需要保证数据有一定的结构，这导致设计和参数化自回归模型非常困难。扩散模型的训练启发了自回归模型的训练，通过特定的训练方式避免了设计的困难。

E. Energy-based model直接对原始数据的分布建模，但直接建模导致学习和采样都比较困难。通过使用扩散恢复似然，模型可以先对样本加入微小的噪声，再从有略微噪声的样本分布来推断原始样本的分布，使的学习和采样过程更简单和稳定。

七． 扩散模型的应用

在下面的每个小节中，我们分别介绍了扩散模型在计算机视觉、自然语言处理、波形信号处理、多模态学习、分子图生成、时间序列以及对抗学习等七大应用方向中的应用，并对每类应用中的方法进行了细分并解析。例如在计算机视觉中可以用diffusion model进行图像补全修复（RePaint）：

在多模态任务中可以用diffusion model进行文本到图像的生成（GLIDE）：

还可以在分子图生成中用diffusion model进行药物分子和蛋白质分子的生成（GeoDiff）：

应用分类汇总见表：

VAE\GAN\FLOW\DDPM\SDE技术区别

总结：

1.数学建模为随机分布，忽略了输入数据分布逐步转化到最后生成图片的随机过程，只关心输入数据分布到生成数据分布的转化分布。

a.自回归模型 b.变分自编码器. c.正则化流模型 d.生成对抗网络

2.数学建模为随机过程，输入数据分布经历了一个过程逐步转化成最终生成图片，对转化的随机过程也考虑进去，用T步随机噪声过程来模拟（扩散模型家族）。

a.DDIM b.SDE c.stable diffusion

3.从Auto encode到VAE，是对数据样本做了分布假设，不是单个数据点，输入数据是一个分布。增加输入多样性，让学习更难增加模型输出的鲁棒性。

4.GAN的不稳定性来源于，对数据样本分布没做任何约束、同时对随机分布也没做任何约束，可以认为是随机分布建模生成的最朴素方法。所以模型的表达力很强，但是可控性不太好

5.Flow其实已经有对生成过程约束的意思了，只是没有引入随机工程数学建模，所以flow可控性比较好

通俗理解

现在我们通过一个比喻来说明它们之间的区别。我们把数据的生成过程，也就是从Z映射到X的过程，比喻为过河。河的左岸是Z，右岸是X，过河就是乘船从左岸码头到达右岸码头。船可以理解为生成模型，码头的位置可以理解为样本点Z或者X在分布空间的位置。不同的生成模型有不同的过河的方法，如下图所示（图中小圆点代表样本点，大圆圈代表样本分布，绿色箭头表示loss），我们分别来分析。

不同生成模型的过河方式

1. GAN的过河方式

从先验分布随机采样一个Z，也就是在左岸随便找一个码头，直接通过对抗损失的方式强制引导船开到右岸，要求右岸下船的码头和真实数据点在分布层面上比较接近。

2. VAE的过河方式

1）VAE在过河的时候，不是强制把河左岸的一个随机点拉到河右岸，而是考虑右岸的数据到达河左岸会落在什么样的码头。如果知道右岸数据到达左岸大概落在哪些码头，我们直接从这些码头出发就可以顺利回到右岸了。

2）由于VAE编码器的输出是一个高斯分布的均值和方差，一个右岸的样本数据X到达河左岸的码头位置不是一个固定点，而是一个高斯分布，这个高斯分布在训练时会和一个先验分布（一般是标准高斯分布）接近。

3）在数据生成时，从先验分布采样出来的Z也大概符合右岸过来的这几个码头位置，通过VAE解码器回到河右岸时，大概能到达真实数据分布所在的码头。

3. Flow的过河方式

1）Flow的过河方式和VAE有点类似，也是先看看河右岸数据到河左岸能落在哪些码头，在生成数据的时候从这些码头出发，就比较容易能到达河右岸。

2）和VAE不同的是，对于一个从河右岸码头出发的数据，通过Flow到达河左岸的码头是一个固定的位置，并不是一个分布。而且往返的船开着双程航线，来的时候从什么右岸码头到达左岸码头经过什么路线，回去的时候就从这个左岸码头经过这个路线到达这个右岸码头，是完全可逆的。

3）Flow需要约束数据到达河左岸码头的位置服从一个先验分布（一般是标准高斯分布），这样在数据生成的时候方便从先验分布里采样码头的位置，能比较好的到达河右岸。

4. Diffusion的过河方式

1）Diffusion也借鉴了类似VAE和Flow的过河思想，要想到达河右岸，先看看数据从河右岸去到左岸会在哪个码头下船，然后就从这个码头上船，准能到达河右岸的码头。

2）但是和Flow以及VAE不同的是，Diffusion不只看从右岸过来的时候在哪个码头下船，还看在河中央经过了哪些桥墩或者浮标点。这样从河左岸到河右岸的时候，也要一步一步打卡之前来时经过的这些浮标点，能更好约束往返的航线，确保到达河右岸的码头位置符合真实数据分布。

3）Diffusion从河右岸过来的航线不是可学习的，而是人工设计的，能保证到达河左岸的码头位置，虽然有些随机性，但是符合一个先验分布（一般是高斯分布），这样方便我们在生成数据的时候选择左岸出发的码头位置。

4）因为训练模型的时候要求我们一步步打卡来时经过的浮标，在生成数据的时候，基本上也能遵守这些潜在的浮标位置，一步步打卡到达右岸码头。

5）如果觉得开到河右岸一步步这样打卡浮标有点繁琐，影响船的行进速度，可以选择一次打卡跨好几个浮标，就能加速船行速度，这就对应diffusion的加速采样过程。

5. AR的过河方式

1）可以类比Diffusion模型，将AR生成过程 X0,X0:1,…,X0:t,X0:t+1,…,X0:T 看成中间的一个个浮标。从河右岸到达河左岸的过程就好比自回归分解，将 X0:T 一步步拆解成中间的浮标，这个过程也是不用学习的。

2）河左岸的码头 X0 可以看成自回归生成的第一个START token。AR模型河左岸码头的位置是确定的，就是START token对应的embedding。

3）在训练过程中，自回归模型也一个个对齐了浮标，所以在生成的时候也能一步步打卡浮标去到河右岸。

4）和Diffusion不同的是，自回归模型要想加速，跳过某些浮标，就没有那么容易了，除非重新训练一个semi-autoregressive的模型，一次生成多个token跨过多个浮标。

5）和Diffusion类似的是，在训练过程中都使用了teacher-forcing的方式，以当前步的ground-truth浮标位置为出发点，预测下一个浮标位置，这也降低了学习的难度，所以通常来讲，自回归模型和Diffusion模型训练起来都比较容易。