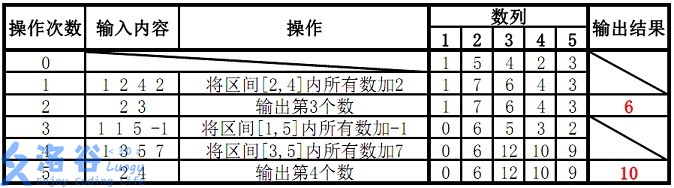
目标检测 回归损失函数
- 1、Smooth L1 Loss
- 2、 IoU Loss
- 3、 GIoU Loss (Generalized-IoU Loss)
- 4、 DIoU Loss (Distance-IoU Loss)
- 5、 CIoU Loss (Complete-IoU Loss)
- 总结:
目标检测任务的损失函数由 Classificition Loss 和 Bounding Box Regeression Loss 两部分构成。
本文介绍目标检测任务中近几年来Bounding Box Regression Loss Function的演进过程,其演进路线是:
Smooth L1 Loss
→
\rightarrow
→ IoU Loss
→
\rightarrow
→ IoU Loss
→
\rightarrow
→ GIoU Loss
→
\rightarrow
→ DIoU Loss
→
\rightarrow
→ CIoU Loss
本文亦按照此路线进行讲解。
1、Smooth L1 Loss
本方法由微软rgb大神提出,Fast RCNN论文提出该方法
1)假设x为预测框和真实框之间的数值差异,常用的 L1 loss、L2 Loss 和 smooth L1 loss 定义分别为:
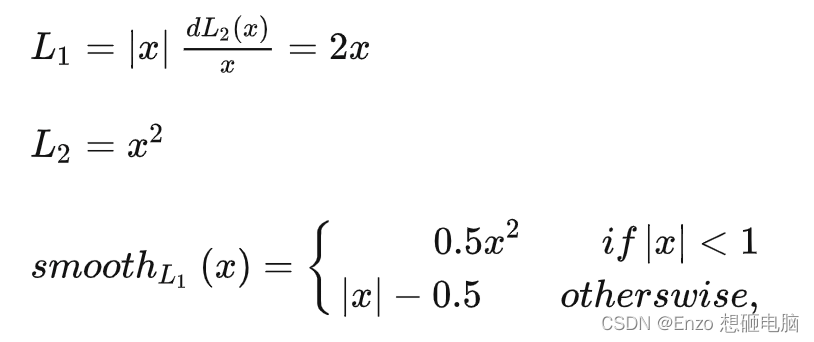
2)上述的3个损失函数对x的导数分别为:

从损失函数对x的导数可知:
- L 1 L1 L1 损失函数对 x x x 的导数为常数,在训练后期, x x x很小时,如果 learning rate 不变,损失函数会在稳定值附近波动,很难收敛到更高的精度。
- L 2 L2 L2 损失函数对x的导数在x值很大时,其导数也非常大,在训练初期不稳定。
- s m o o t h L 1 smooth_{L1} smoothL1 完美的避开了 L 1 L1 L1 和 L 2 L2 L2损失的缺点。
3)实际目标检测框回归任务中的损失 loss 为: L l o c ( t u , v ) = ∑ i ∈ ( x , y , w , h ) s m o o t h L 1 ( t i u − v i ) L_{loc(t^u, v)} = \sum_{i \in (x, y, w, h)}smooth_{L1}(t_i^u - v_i) Lloc(tu,v)=∑i∈(x,y,w,h)smoothL1(tiu−vi)
其中:
- v = ( v x , v y , v w , v h ) v = (v_x, v_y,v_w, v_h) v=(vx,vy,vw,vh) :表示GT 的框坐标,
- t u = ( t x u , t y u , t x w , t h u ) t^u = (t^u_x, t^u_y, t^w_x, t^u_h) tu=(txu,tyu,txw,thu):表示预测的框坐标,即分别求4个点的loss,然后相加作为Bounding Box Regression Loss。

缺点:
- 上面的三种Loss用于计算目标检测的Bounding Box Loss时,独立的求出4个点的Loss,然后进行相加得到最终的Bounding Box Loss,这种做法的假设是4个点是相互独立的,实际是有一定相关性的
- 实际评价框检测的指标是使用IOU,这两者是不等价的,多个检测框可能有相同大小的
Loss,但IOU可能差异很大,为了解决这个问题就引入了IOU LOSS。
2、 IoU Loss
- 本文由旷视提出,发表于2016 ACM
1)通过4个坐标点独立回归Building boxes的缺点:
- 检测评价的方式是使用IoU,而实际回归坐标框的时候是使用4个坐标点
如下图所示,L1或者L2 Loss相同的框,其IoU 不是唯一的 (图a. L2 loss 相同; 图b. L1 loss 相同) - 通过4个点回归坐标框的方式是假设4个坐标点是相互独立的,没有考虑其相关性,实际4个坐标点具有一定的相关性
- 基于L1和L2的距离的loss对于尺度不具有不变性

2)基于此提出IoU Loss,其将4个点构成的box看成一个整体进行回归:

3、 GIoU Loss (Generalized-IoU Loss)
由斯坦福学者提出,发表于CVPR2019
1) IoU Loss 有2个缺点:
- 当预测框和目标框不相交时, I o U ( A , B ) = 0 IoU(A,B)=0 IoU(A,B)=0 时,不能反映 A, B 距离的远近,此时损失函数不可导,IoU Loss 无法优化两个框不相交的情况。 L o s s = − l n I o U , ∂ l o s s ∂ I o U = ( − l n I o U ) ′ = − 1 I o U Loss=-ln^{IoU}, \quad\quad \frac{\partial loss}{\partial IoU} = (-ln^{IoU})' = -\frac{1}{IoU} Loss=−lnIoU,∂IoU∂loss=(−lnIoU)′=−IoU1
- IoU值不能反映两个框是如何相交的:即使两个框的 I o U IoU IoU 值是相同的,其相交方式也可能很不一样。

2) GIoU :Generalized-IoU Loss

最后,损失可以用下面的公式来计算: L G I o U = 1 − G I o U L_{GIoU} = 1 - GIoU LGIoU=1−GIoU
\quad
3)C 的面积的求解
假设有两个任意的 bbox A和B,我们要找到一个最小的封闭形状C,让C可以将A和B包围在里面。
A = ( x m i n A , x m a x A , y m i n A , y m a x A ) A = (x_{min}^A, x_{max}^A, y_{min}^A, y_{max}^A) A=(xminA,xmaxA,yminA,ymaxA)
B = ( x m i n B , x m a x B , y m i n B , y m a x B ) B = (x_{min}^B, x_{max}^B, y_{min}^B, y_{max}^B) B=(xminB,xmaxB,yminB,ymaxB)
则, C 的坐标为:
x m i n C = m i n ( x m i n A , x m i n B ) , x m a x C = m a x ( x m a x A , x m a x B ) x_{min}^C = min(x_{min}^A, x_{min}^B), \quad x_{max}^C = max(x_{max}^A, x_{max}^B) xminC=min(xminA,xminB),xmaxC=max(xmaxA,xmaxB)
y m i n C = m i n ( y m i n A , y m i n B ) , y m a x C = m a x ( y m a x A , y m a x B ) y_{min}^C = min(y_{min}^A, y_{min}^B), \quad y_{max}^C = max(y_{max}^A, y_{max}^B) yminC=min(yminA,yminB),ymaxC=max(ymaxA,ymaxB)
C 的面积为:
A
r
e
a
C
=
(
x
m
a
x
C
−
x
m
i
n
C
)
∗
(
y
m
a
x
C
−
y
m
i
n
C
)
Area^C = (x_{max}^C - x_{min}^C) * (y_{max}^C - y_{min}^C)
AreaC=(xmaxC−xminC)∗(ymaxC−yminC)
\quad
4)GIoU 相比于 IoU 有如下性质:
- 和原始的 loU 类似,GIoU具有尺度不变性 ( GloU 对物体的尺度大小不敏感,因为使用的是比值的原因)
-
0
≤
=
I
o
U
<
=
1
,
0
<
=
C
−
(
A
∪
B
)
C
<
1
0≤= IoU <=1,0 <= \frac{C - (A \cup B)}{C} <1
0≤=IoU<=1,0<=CC−(A∪B)<1,
L
G
I
o
U
=
1
−
G
I
o
U
L_{GIoU} = 1 - GIoU
LGIoU=1−GIoU, 所以
−
1
<
G
I
O
U
<
=
1
-1 < GIOU <= 1
−1<GIOU<=1
- 当 A 和 B 完全重合时:IoU = GIoU = 1
- 当 A,B 不重合时, I o U = 0 , G I o U IoU=0, GIoU IoU=0,GIoU 趋近于 -1, 或者说 当A,B 不重合且 距离无限远时, G I o U = − 1 GIoU = -1 GIoU=−1
GIoU Loss 仍然存在不足:当目标框 完全包裹 预测框的时候,IoU 和 GIoU 的值一样,此情况下 GIoU 退化为 IoU, 无法区分其相对位置关系。

基于IoU和GIoU存在的问题,有两个方向 值得思考:
- 第一:直接最小化预测框与目标框之间的归一化距离是否可行,以达到更快的收敛速度。
- 第二:如何使回归在与目标框有重叠甚至包含时更准确、更快。
好的目标框回归损失应该考虑三个重要的几何因素:重叠面积,中心点距离,长宽比。
- DIoU Loss:考虑了重叠面积和中心点距离,相对于GIoU Loss收敛速度更快,但没有考虑到长宽比;
- CIoU Loss,以上三个因素都考虑到了, 其收敛的精度更高。
4、 DIoU Loss (Distance-IoU Loss)
本文发表在AAAI 2020
- 通常基于 IoU-based 的 loss 可以定义为 L = 1 − I o U + R ( B , B g t ) L =1- IoU + R(B, B^{gt}) L=1−IoU+R(B,Bgt),其中 R ( B , B g t ) R(B, B^{gt}) R(B,Bgt) 定义为预测框 B B B 和目标框 B g t B^{gt} Bgt 的惩罚项。
-
D
I
o
U
DIoU
DIoU 中的惩罚项表示为
R
D
I
o
U
=
ρ
2
(
b
,
b
g
t
)
c
2
R_{DIoU} = \frac{\rho ^2(b, b^{gt})}{c^2}
RDIoU=c2ρ2(b,bgt),其中
b
b
b 和
b
g
t
b^{gt}
bgt分别表示 B$ 和
B
g
t
B^{gt}
Bgt 的中心点,
ρ
\rho
ρ 表示欧式距离,C表示
B
B
B和
B
g
t
B^{gt}
Bgt 的最小外界矩形的对角线距离,如下图所示。可以将DIoU替换 IoU 用于 NMS算法当中,也即论文提出的DIoU-NMS,实验结果表明有一定的提升。
• DloU Loss function 定义为: L D I o U = 1 − I o U + ρ 2 ( b , b g t ) c 2 L_{DIoU} = 1- IoU + \frac{\rho ^2(b, b^{gt})}{c^2} LDIoU=1−IoU+c2ρ2(b,bgt)

DIoU的性质:
- 尺度不变性
- 当两个框完全重合时,
L
I
o
U
=
L
G
I
o
U
=
L
D
I
o
U
=
0
L_{IoU} = L_{GIoU} = L_{DIoU} = 0
LIoU=LGIoU=LDIoU=0
当两个框不相交时 - DIoU Loss 可以直接优化 2个框直接的距离,比 GIoU Loss 收敛速度更快
- 对于目标框包裹预测框的这种情况,DIoU Loss 可以收敛的很快,而 GIoU Loss此时退化为IoU Loss收敛速度较慢
5、 CIoU Loss (Complete-IoU Loss)
1)CIoU的惩罚项是在DIoU的惩罚项基础上加了一个影响因子 α v \alpha v αv, 这个因子把预测框长宽比拟合目标框的长宽比考虑进去。
R C I o U = ρ 2 ( b , b g t ) c 2 + α v R_{CIoU} = \frac{\rho ^2(b, b^{gt})}{c^2} +\alpha v RCIoU=c2ρ2(b,bgt)+αv, 其中:
-
α \alpha α 是用于做 trade-off 的参数, α = v ( 1 − I o U ) + v \alpha = \frac{v}{(1-IoU)+v} α=(1−IoU)+vv
-
v v v是用来衡量长宽比一致性的参数, v = 4 π 2 ( a r c t a n w g t h g t − a r c t a n w h ) 2 v = \frac{4}{\pi^2}(arctan \frac{w^{gt}}{h^{gt}} - arctan \frac{w}{h})^2 v=π24(arctanhgtwgt−arctanhw)2
CIoU Loss function的定义为: L D I o U = 1 − I o U + ρ 2 ( b , b g t ) c 2 + α v L_{DIoU} = 1- IoU + \frac{\rho ^2(b, b^{gt})}{c^2} +\alpha v LDIoU=1−IoU+c2ρ2(b,bgt)+αv
2)DIoU和CIoU的提升效果

总结:
(1)Smooth L1 Loss

(2)loU Loss : L o s s = − l n I o U Loss=-ln^{IoU} Loss=−lnIoU
(3)GloU Loss : L G I o U = 1 − I o U + C − ( A ∩ B ) ∣ C ∣ L_{GIoU} = 1 - IoU + \frac{C - (A \cap B)}{|C|} LGIoU=1−IoU+∣C∣C−(A∩B)
(4)DloU Loss: L D I o U = 1 − I o U + ρ 2 ( b , b g t ) c 2 L_{DIoU} = 1- IoU + \frac{\rho ^2(b, b^{gt})}{c^2} LDIoU=1−IoU+c2ρ2(b,bgt)
(5)CIoU Loss : L D I o U = 1 − I o U + ρ 2 ( b , b g t ) c 2 + α v L_{DIoU} = 1- IoU + \frac{\rho ^2(b, b^{gt})}{c^2} +\alpha v LDIoU=1−IoU+c2ρ2(b,bgt)+αv
参考文章:
1、目标检测回归损失函数简介
2、目标检测算法之CVPR2019 GIoU Loss
![[软件工程导论(第六版)]第3章 需求分析(课后习题详解)](https://img-blog.csdnimg.cn/4c778e1d5cb54e648742e2fea5fe8afc.png)