摘要

1237. 找出给定方程的正整数解

一、暴力求解

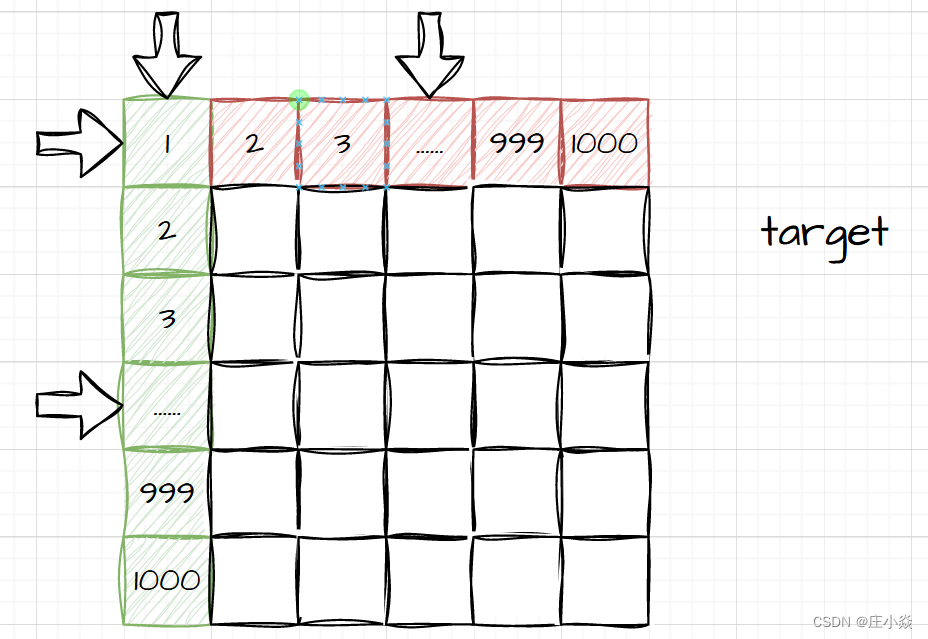
根据题目给出的x和y的取值范围，枚举所有的 x,y数对，保存满足f(x,y)=z的数对，最后返回结果。

    /**
     * @description 使用的暴力法 直接遍历符合的就添加到结果中
      * @param: customfunction
     * @param: z
     * @date: 2023/2/18 9:20
     * @return: java.util.List<java.util.List<java.lang.Integer>>
     * @author: xjl
    */
    public List<List<Integer>> findSolution(CustomFunction customfunction, int z) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        for (int x = 1; x <= 1000; x++) {
            for (int y = 1; y <= 1000; y++) {
                if (customfunction.f(x, y) == z) {
                    List<Integer> pair = new ArrayList<Integer>();
                    pair.add(x);
                    pair.add(y);
                    res.add(pair);
                }
            }
        }
        return res;
    }

复杂度分析

时间复杂度：O(mn)，其中m是x的取值数目，n是y的取值数目。
空间复杂度：O(1)。返回值不计入空间复杂度。

二、二分查找

当我们固定 x=x0时，函数 g(y)=f(x0,y)是单调递增函数，可以通过二分查找来判断是否存在 y=y0，使 g(y0)=f(x0,y0)=z成立。

    /**
     * @description 使用的二分法来是实现
      * @param: customfunction
     * @param: z
     * @date: 2023/2/18 9:20
     * @return: java.util.List<java.util.List<java.lang.Integer>>
     * @author: xjl
    */
    public List<List<Integer>> findSolution2(CustomFunction customfunction, int z) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        for (int x = 1; x <= 1000; x++) {
            int yleft = 1, yright = 1000;
            while (yleft <= yright) {
                int ymiddle = (yleft + yright) >> 1;
                if (customfunction.f(x, ymiddle) == z) {
                    List<Integer> pair = new ArrayList<Integer>();
                    pair.add(x);
                    pair.add(ymiddle);
                    res.add(pair);
                    break;
                }
                if (customfunction.f(x, ymiddle) > z) {
                    yright = ymiddle - 1;
                } else {
                    yleft = ymiddle + 1;
                }
            }
        }
        return res;
    }

复杂度分析

时间复杂度：O(mlog⁡n)，其中m是x的取值数目，n是y的取值数目。
空间复杂度：O(1)。返回值不计入空间复杂度。

三、双指针求解

假设 x1<x2，且 f(x1,y1)=f(x2,y2)=z，显然有 y1>y2。因此我们从小到大进行枚举x，并且从大到小枚举y，当固定x 时，不需要重头开始枚举所有的y，只需要从上次结束的值开始枚举即可。

/**
     * @description 使用双指针来实现 固定x 来找到y 然后x增加 y必然要减少f(x,y)=z
      * @param: customfunction
     * @param: z
     * @date: 2023/2/18 9:28
     * @return: java.util.List<java.util.List<java.lang.Integer>>
     * @author: xjl
    */
    public List<List<Integer>> findSolution3(CustomFunction customfunction, int z) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        for (int x = 1, y = 1000; x <= 1000 && y >= 1; x++) {
            while (y >= 1 && customfunction.f(x, y) > z) {
                y--;
            }
            if (y >= 1 && customfunction.f(x, y) == z) {
                List<Integer> pair = new ArrayList<Integer>();
                pair.add(x);
                pair.add(y);
                res.add(pair);
            }
        }
        return res;
    }

复杂度分析

时间复杂度：O(m+n)，其中m是x的取值数目，n是y的取值数目。
空间复杂度：O(1)。返回值不计入空间复杂度。

四、搜索二维矩阵的目标值

240. 搜索二维矩阵 II

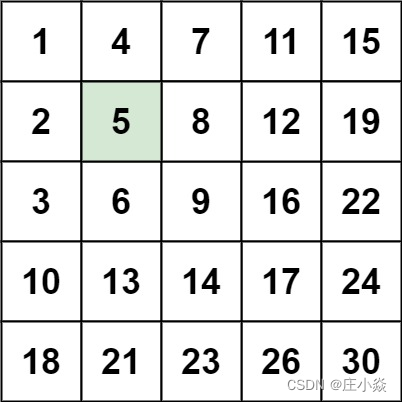
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

4.1 暴力求解

我们直接遍历整个矩阵matrix，判断target是否出现即可。

    /**
     * @description 直接暴力的方法 但是一般都是超时结果
      * @param: matrix
     * @param: target
     * @date: 2023/2/18 9:48
     * @return: boolean
     * @author: xjl
    */
    public boolean searchMatrix(int[][] matrix, int target) {
        for (int[] arr:matrix){
            for (int i:arr){
                if (i==target){
                    return true;
                }
            }
        }
        return false;
    }

复杂度分析

时间复杂度：O(mn)。
空间复杂度：O(1)。

4.2 利用二分查找算法求解

   /**
     * @description 利用二分法来 因为每一行都是递增的
      * @param: matrix
     * @param: target
     * @date: 2023/2/18 9:49
     * @return: boolean
     * @author: xjl
    */
    public boolean searchMatrix2(int[][] matrix, int target) {
        for (int[] arr:matrix){
            // 调用了系统的二分法来实现
            if (Arrays.binarySearch(arr,target)>=0){
                return true;
            }
        }
        return false;
    }

复杂度分析

时间复杂度：O(mlog⁡n)。对一行使用二分查找的时间复杂度为 O(log⁡n)，最多需要进行 m次二分查找。
空间复杂度：O(1)。

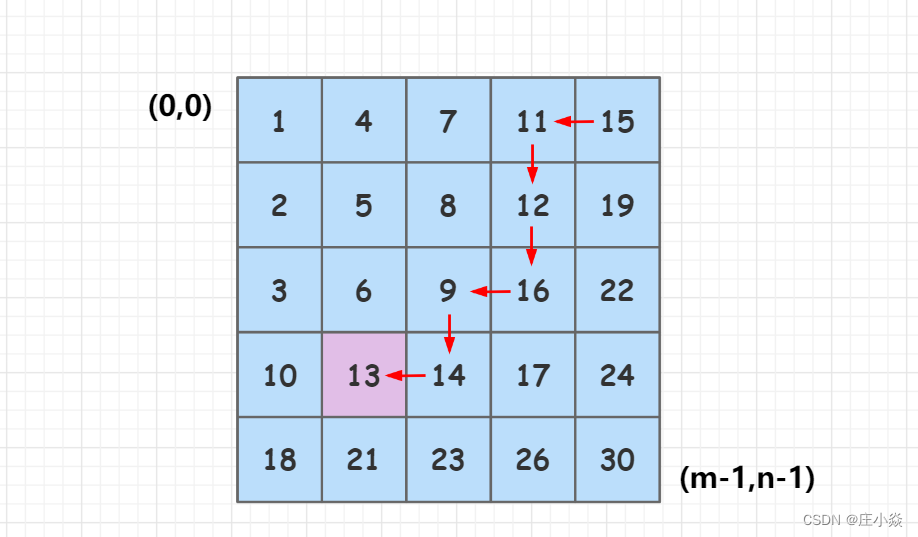
4.3 单调性扫描求解

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length, n = matrix[0].length;
        int x = 0, y = n - 1;
        while (x < m && y >= 0) {
            if (matrix[x][y] == target) {
                return true;
            }
            if (matrix[x][y] > target) {
                --y;
            } else {
                ++x;
            }
        }
        return false;
    }
}

复杂度分析