1.题目链接:123. 买卖股票的最佳时机 III
题目描述:
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
解法:
①定义dp数组,dp[i][0]表示未操作的时候的钱数,dp[i][1]表示第一次持有的钱数,dp[i][2]表示第一次不持有的钱数,dp[i][3]表示第二次持有的钱数,dp[i][4]表示第二次不持有的钱数。
②递推公式:
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])---即第一次持有 = max(前一天第一次持有,前一天没操作今天持有)
dp[i][2] = max(dp[i-1][2], dp[i-1][1] + prices[i])---即第一次不持有 = max(前一天第一次不持有,前一天第一次持有今天卖了)
dp[i][3] = max(dp[i-1][3], dp[i-1][2] - prices[i])---即第二次持有 = max(前一天第二次持有,前一天第一次不持有今天持有)
dp[i][4] = max(dp[i-1][4], dp[i-1][3] + prices[i])---即第二次不持有 = max(前一天第二次不持有,前一天第二次持有今天卖了)
③初始化:因为我们根据前一天求的当前的值,所以初始化dp[0][0~4],dp[1],dp[3] = -prices[0];dp[0],dp[2],dp[4] = 0;
④遍历顺序:因为根据前一天值求的,所以要从小到大遍历。
⑤最后返回最后一天最后一次不持有的状态的值 = 最大钱数。因为最后一次不持有肯定覆盖了前面不持有的钱数。
下面为代码(java):

2.题目链接:188. 买卖股票的最佳时机 IV
题目描述:
给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
解法:
①此题和上题的不同就是将2抽象成了k。上一题中最多可以完成2笔交易,状态就有5个即从0~4,那么有k笔交易,状态就有2k+1个即从0~2k。
②故我们创建dp[prices.length][2k+1]
③递推公式:
不论是多少次交易我们每次都要求持有和不持有的状态,那么共要求2k+1个状态,我们就要有个循环来求状态 即j = 0开始,到哪结束呢?eg:2次最后的状态是4,我们要让j每两步两步的跳(即每一次都求出持有和不持有的状态),所以当j = 2k-1的时候正好能求出2k和2k+1的状态。所以j < 2k,j+=2.
故递推公式:
for(int j = 0; j < 2k;j += 2){
dp[i][j+1] = max(dp[i-1][j+1], dp[i-1][j] - prices[i]);---即买入 = max(前一天买入,前一天没操作当天买入)
dp[i][j+2] = max(dp[i-1][j+2], dp[i-1][j+1] + prices[i])---即卖出 = max(前一天卖出,前一天买入当天卖出)
}
④初始化:
根据递推公式根据前一天的值求的,所以初始化dp[0][0~2k],因为只有买入的时候是-prices[i]。故初始化只有下标为奇数的时候为-prices[0],其余为0即可。
⑤遍历顺序:
根据递推公式根据前一天的值求当前值,所以从前向后遍历。
⑥最后返回最后一天的最后一次卖出的状态即为求的最大利润。
下面为代码(java):
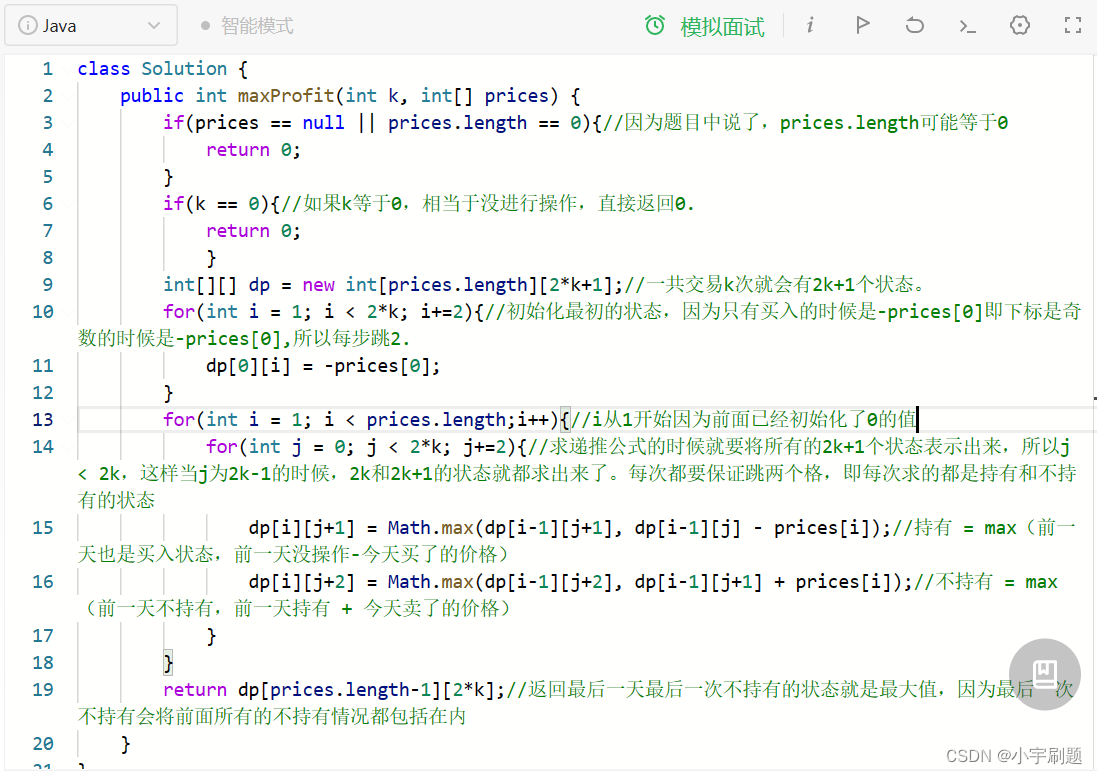
3.总结:
①第一题是股票可以买卖2次,可以列出5个状态分别是什么,当然也可以初始化具体5个状态。递推公式都是根据前一个的状态来求的。最后返回的是最后一天的最后一次不持有的状态。
②第二题就是将2抽象成了k,所以在求递推公式的时候,我们要每一次求出买和卖两个状态,然后用循环来做,每次跳两步即可。在初始化的时候同理要用循环来初始化,然后只有买入的状态初始化为-prices[0],其余的都为0.
③现在做了股票买卖系列的:只能买卖一次,可以买卖多次,至多买卖两次,至多买卖k次。






![[Linux篇] Linux常见命令和权限](https://img-blog.csdnimg.cn/2caf27c59873404fbe70a89c7e5109f5.png#pic_center)