平衡二叉树

题目详细：LeetCode.110

由题可知：一个平衡二叉树需要满足，其每个节点的左右两个子树的高度差的绝对值不超过 1 。

我们可以依照题意，直接来一波模拟：

利用层序遍历（或其他遍历方法）遍历每一个节点
通过计算每一个节点的左右子树的高度差来判断是否为平衡二叉树

那么这道题的难点就在于：如何计算树的高度？亦或是如何计算当前节点的高度？

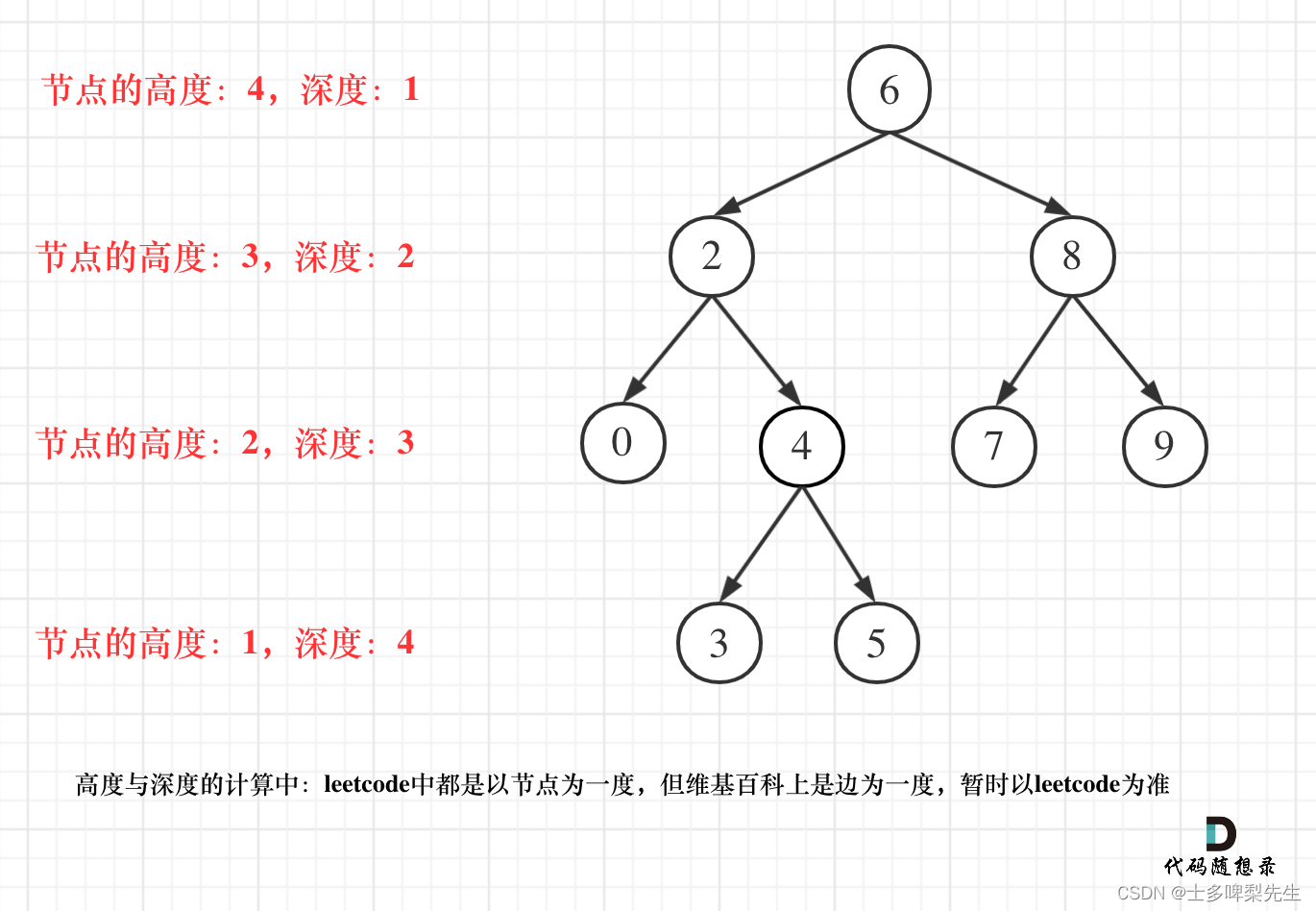
在这里插入图片描述

由图及二叉树的概念可知，二叉树的高度和深度是两个不同的定义：

二叉树的深度：指从根节点到当前节点的最长简单路径边数（从上往下计算）
二叉树的高度：指从当前节点到叶子节点的最长简单路径边数（从下往上计算）

由此我们可以得到计算二叉树深度和高度的遍历方式：

计算二叉树的深度，需要从上到下去访问节点，所以使用前序遍历（根左右）
计算二叉树的高度，需要从下到上去访问节点，所以使用后序遍历（左右根）

Java解法（模拟，迭代，层序遍历节点，后序遍历计算树的高度）：

class Solution {
    public boolean isBalanced(TreeNode root) {
        if(null == root) return true;
        return this.bfs(root);
    }

    public int getHeight(TreeNode root){
        Stack<TreeNode> stack = new Stack<>();
        if(null != root) stack.push(root);
        int res = 0, height = 0;
        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            if(null != node){
                stack.push(node);
                stack.push(null);
                height++;
                if(null != node.right) stack.push(node.right);
                if(null != node.left) stack.push(node.left);
            }else{
                node = stack.pop();
                height--;
            }
            res = Math.max(res, height);
        }
        return res;
    }

    public boolean bfs(TreeNode root){
        Queue<TreeNode> queue = new LinkedList<>();
        if(null != root) queue.offer(root);
        while(!queue.isEmpty()){
            int n = queue.size();
            while(n-- > 0){
                TreeNode node = queue.poll();
                if(Math.abs(this.getHeight(node.left) - this.getHeight(node.right)) > 1) return false;
                if(null != node.left) queue.offer(node.left);
                if(null != node.right) queue.offer(node.right);
            }
        }
        return true;
    }
}

通过之前的练习和解题过程，我们可以发现：

计算二叉树的高度的算法和计算二叉树的深度的算法很相似
计算二叉树的深度使用后序遍历也可也得到正确的结果
计算二叉树的高度差，其实和计算二叉树的深度差是一样的结果，只是在定义上不同

当然此题用迭代法，其实效率很低，因为没有很好的模拟回溯的过程，所以迭代法有很多重复的计算。
虽然理论上所有的递归都可以用迭代来实现，但是有的场景难度可能比较大。
众所周知，都知道回溯法其实就是递归，但是很少人用迭代的方式去实现回溯算法！

迭代法虽然能够非常清晰的根据平衡二叉树的特点来解题，但是在遍历过程中存在着许多重复的计算，例如重复计算节点的高度。

用递归的方法来实现回溯的过程，能够更有效率地来解决这道题：

Java解法（递归）：

class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null){
            return true;
        }
        int leftHeight = getHeight(root.left, 1);
        int rightHeight = getHeight(root.right, 1);
        return Math.abs(leftHeight - rightHeight) <= 1 
            && isBalanced(root.left) 
            && isBalanced(root.right);
    }

    private int getHeight(TreeNode root, int height){
        if(root == null){
            return height;
        }
        int leftHeight = getHeight(root.left, height+1);
        int rightHeight = getHeight(root.right, height+1);
        return Math.max(leftHeight, rightHeight);
    }
}

上述代码只是将模拟的过程转为递归写法，虽然利用&&的短路效应也得到了提升算法效率的目的，但不能很明显的体现出回溯的特点。

而且如果当前传入节点为根节点的二叉树已经不是二叉平衡树了，还返回高度的话就没有意义了。

所以如果已经不是二叉平衡树了，可以返回 -1 来标记当前节点已经不符合平衡树的规则了，不需要往后再进行递归操作。

Java解法（递归，优化）：

class Solution {
    public boolean isBalanced(TreeNode root) {
        if(null == root) return true;
        return this.getHeight(root) == -1 ? false : true;
    }

    public int getHeight(TreeNode root){
        if(null == root) return 0;
        int leftHeight = this.getHeight(root.left);
        if(leftHeight == -1) return -1;
        int rightHeight = this.getHeight(root.right);
        if(rightHeight == -1) return -1;
        // 分别求出其左右子树的高度，然后如果差值绝对值小于等于1，则返回当前二叉树的高度，否则返回-1，表示已经不是二叉平衡树了。
        return Math.abs(leftHeight - rightHeight) > 1 ? -1 : 1 + Math.max(leftHeight, rightHeight);
    }
}

二叉树的所有路径

题目详细：LeetCode.257

题目要求找到从根节点到叶子节点的所有路径，使用前序遍历，能够方便地让父节点指向孩子节点，找到对应的路径。

确定了遍历顺序为前序遍历后，接下来就是对节点的处理逻辑：

要求输出二叉树从根节点到叶子节点的路径，那么我们就需要在遍历过程中，利用列表记录路径上经过的节点
当遇到叶子节点时，则可确定一条路径，按照要求的格式将路径列表转为字符串，保存到结果集中
确定了一条路径后，我们需要回溯，也就是回退一个节点并尝试寻找另一条路径
- 如果不进行回溯，则可能在其他路径记录中出现重复的节点
直到每一个节点都经过了访问和回溯过程，没有其他节点可以访问时，回溯停止，说明找到了二叉树的所有路径。

Java解法（递归，回溯过程明显化）：

class Solution {
    private List<String> ans = new ArrayList<>();

    public List<String> binaryTreePaths(TreeNode root) {
        List<TreeNode> path = new ArrayList<>();
        if(null == root) return this.ans;
        this.traversal(root, path);
        return ans;
    }

    public void traversal(TreeNode root, List<TreeNode> path){
        if(null == root) return;
        path.add(root);
        if(null == root.left && null == root.right){
            String path_str = path.stream().map(node -> String.valueOf(node.val)).collect(Collectors.joining("->"));
            this.ans.add(path_str);
            return;
        }
        if(null != root.left){
            this.traversal(root.left, path);
            // 回溯
            path.remove(path.size() - 1);
        }
        if(null != root.right){
            this.traversal(root.right, path);
            // 回溯
            path.remove(path.size() - 1);
        }
    }
}

递归完，就要做回溯，因为 path 是引用传递，需要删节点后才能加入新的节点，否则会重复出现其他路径的节点。
回溯和递归应该是一一对应的，有一个递归，就要有一个回溯。

在之前的许多练习中，其实用到了递归也就已经用到了回溯，只是没办法很明显的体现出来。

所以在这道题的解题过程中，我们用List来存储路径上的节点，其实也可以用String直接来存储到达叶子节点的路径，只是用List来存储之后，在每次递归完成后都需要remove已经过的节点，能够非常明显地看到回溯的过程。

那么假设我们用String来作为递归参数，存储路径的话，应该要这么写：

Java解法（递归，简洁版，隐藏了回溯过程）：

class Solution {
    private List<String> ans = new ArrayList<>();

    public List<String> binaryTreePaths(TreeNode root) {
        this.traversal(root, null);
        return ans;
    }

    public void traversal(TreeNode root, String path){
        if(null == path){
            path = String.valueOf(root.val);
        }else{
            path += String.valueOf(root.val);
        }
        if(null == root.left && null == root.right){
            this.ans.add(path);
            return;
        }
        if(null != root.left){
            this.traversal(root.left, path + "->");
        }
        if(null != root.right){
            this.traversal(root.right, path + "->");
        }
    }
}

左叶子之和

题目详细：LeetCode.404

由题目和示例可知：

求叶子节点之和，但这个叶子节点，要求是树的左节点
空树视为没有节点，只有一个节点的树的根节点不视作左节点。

在递归函数中，我增加了一个标识参数 isLeft ，来标识当前节点是否为树的左节点

那么我们只需要遍历树中的每一节点，找到满足以下两个条件的节点即可：

找到叶子节点：root.left == null && root.right == null
节点是左节点：isLeft == true

累计满足条件的节点的属性数值即可得到左叶子之和，这样的递归方式适合全部的遍历顺序。

Java解法（递归，易理解版）：

class Solution {
    public int sum = 0;

    public int sumOfLeftLeaves(TreeNode root) {
        this.traversal(root, false);
        return this.sum;
    }

    public void traversal(TreeNode root, boolean isLeft){
        if(root == null) return;
        if(root.left == null && root.right == null){
            if(isLeft) sum += root.val;
            return;
        }
        this.traversal(root.left, true);
        this.traversal(root.right, false);
    }
}

当然如果要应扣遍历顺序的话，因为是求左节点之和，所以优先处理的应该是左节点，所以一般采用后序遍历的顺序（左右根）。

不过解题的思路是相似的，只是在遍历过程中，优先访问了左节点，并判断该左节点是不是叶子节点，如果是叶子节点则累计数值：

Java解法（后序遍历）：

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        return this.traversal(root);
    }

    public int traversal(TreeNode root){
        if(root == null) return 0;
        int leftSum = traversal(root.left);
        TreeNode leftNode = root.left;
        if(leftNode != null && leftNode.left == null && leftNode.right == null){
            leftSum = leftNode.val;
        }
        int rightSum = traversal(root.right);
        int sum = leftSum + rightSum;
        return sum;
    }
}

Java解法（后序遍历，简约版）：

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        return this.traversal(root);
    }

    public int traversal(TreeNode root){
        if(root == null) return 0;
        int leftNum = 0;
        TreeNode leftNode = root.left;
        if(leftNode != null && leftNode.left == null && leftNode.right == null){
            leftNum = leftNode.val;
        }
        return leftNum + this.traversal(root.left) + this.traversal(root.right);
    }
}