目录
1.什么是主成分分析
2.什么是Thile指数(锡尔系数),是用来干什么的
3.罗伦次(洛伦兹)曲线的含义,表征什么样的现象
4.什么是偏相关分析,偏相关分析系数的含义,主要作用
5.多元回归分析中,如何去检验识别多重共线性,处理方法,存在多重共线性的后果
6.方差膨胀因子含义,作用
7.什么是空间插值
8.地统计学中,什么是区域化变量,有什么特征
9.什么是主成分回归,含义
10.特征统计中,方差和协方差的概念,区别,联系;标准离差(标准差)和标准误差的概念,区别,联系
11.主成分分析和因子分析的概念,区别,联系
12.什么是协整分析,含义
13.马尔科夫分析中,转移概率的概念;计算一步转移概率矩阵;马尔科夫的特点,无后效性,终极概率
14.相关分析中,什么是典型相关分析,含义
15.统计特征中,偏度和峰度的概念,区别,联系
16.时间序列中,截面数据和面板数据的概念,区别,联系
17.什么是计量地理学,研究对象,研究内容
18.半变异函数中各个参数的含义,并用示意图来表示,函数指标的意义
19.聚类分析中,如何进行系统聚类;什么是模糊聚类,在哪些领域应用
20.主成分分析过程中,特征值,特征向量,载荷之间的关系,写出主成分的表达式
1.什么是主成分分析
主成份分析方法就是用较少的几个综合指标来代替原来较多的指标,而这些较少的综合指标既能尽多地反映原来较多指标的有用信息,且相互之间又是无关的。
2.什么是Thile指数(锡尔系数),是用来干什么的
锡尔系数,用于对经济发展、收入分配等均衡(不均衡)状况,进行定量化的描述。
锡尔系数越大,就表示收入分配差异越大,反之越均衡。
锡尔系数又称锡尔熵,有两个锡尔系数指标,即锡尔系数T和锡尔系数L。
3.罗伦次(洛伦兹)曲线的含义,表征什么样的现象
20世纪初,意大利统计学家罗伦次,首先使用累计频率曲线研究工业化的集中化程度。后来,这种曲线就被称之为罗伦次曲线。
罗伦次曲线显示了数据的集中程度。
4.什么是偏相关分析,偏相关分析系数的含义,主要作用
在对其他变量的影响进行控制的条件下,衡量多个变量中某两个变量之间的线性相关程度的指标称为偏相关系数。
作用:在所有的自变量中,判断哪些自变量对因变量的影响较大,从而选择作为必需的自变量。
5.多元回归分析中,如何去检验识别多重共线性,处理方法,存在多重共线性的后果
多元线性回归模型的检验:①相关系数检验②剩余标准误差③F-检验④t-检验⑤DW检验
识别多重共线性:①直观判断②相关系数判断③VIF判断。
处理方法:①剔除不必要的解释变量②增加观测值③改变自变量的定义形式④寻找新的解释变量⑤采用有偏估计⑥应用逐步回归技术
后果:①降低参数估计的精度②模型参数的敏感性提高③荒谬的结果④有用变量的作用减小
6.方差膨胀因子含义,作用
VIF指的是解释变量之间存在多重共线性时的方差与不存在多重共线性时的方差之比。
作用:可以反映多重共线性导致的方差的增加程度。
若0<=VIF<10,没有多重共线性
若10<VIF<=100,多重共线性较强
若100<=VIF,多重共线性严重
7.什么是空间插值
常用于将离散点的测量数据转换为连续的数据曲面,以便与其它空间现象的分布模式进行比较,它包括了空间内插和外推两种算法。
8.地统计学中,什么是区域化变量,有什么特征
当一个变量呈现一定的空间分布并显示某种特征或现象时,称之为区域化变量。
特征:随机性、结构性
9.什么是主成分回归,含义
以主成分为自变量进行的回归分析,利用主成分将多个指标化为少数几个独立的指标,进而在不丢失重要信息的前提下消除多重共线性的回归分析方法。
10.特征统计中,方差和协方差的概念,区别,联系;标准离差(标准差)和标准误差的概念,区别,联系
方差:方差用以衡量数据的集中或分散程度。
协方差:协方差用以衡量两个变量的协变趋势,即共同离散程度。
区别:方差研究的是一维数据偏离均值的离散状况,协方差研究的是二维数据,即数据之间的相关性。
联系:方差是协方差的一种特殊情况,即当两个变量是相同的情况。
标准离差(标准差):是观测值与均值之间的平均距离。
标准误差:标准误差用以衡量实测数据对预测数据的偏离程度,或者说实测数据相对于回归线的离散程度。
区别:标准差反映的是数据的精确度,标准误差反映的是度量结果的精确度。
联系:两者都是变异指标,从公式上看是两者是正相关;标准误差是特殊的标准离差。
11.主成分分析和因子分析的概念,区别,联系
主成分分析:用较少的几个综合指标来代替原来较多的指标,而这些较少的综合指标既能尽多地反映原来较多指标的有用信息,且相互之间又是无关的。
因子分析:因子分析是主成分分析的推广,也是利用降维的思想,由研究原始变量相关矩阵或协方差矩阵的内部依赖关系出发,把一些具有错综复杂关系的多个变量归结为少数几个综合因子的一种多元统计分析方法。
区别:①主成分分析模型是原始变量的线性组合,是将原始变量加以综合、归纳,仅仅是变量变换;而因子分析是将原始变量加以分解,描述原始变量协方差矩阵结构的模型;只有当提取的公因子个数等于原始变量个数时,因子分析才对应变量变换。
②主成分分析中每个主成分对应的系数是唯一确定的;因子分析中每个因子的相应系数即因子载荷不是唯一的。
③因子分析中因子载荷的不唯一性有利于对公因子进行有效解释;而主成分分析对提取的主成分的解释能力有限。
联系:①因子分析是主成分分析的推广,是主成分分析的逆问题。
②二者都是以“降维”为目的,都是从协方差矩阵或相关系数矩阵出发。
12.什么是协整分析,含义
用来分析变量之间的长期均衡关系,在协整分析两变量的过程中,如果自变量和因变量是协整的,我们就可以确信这两变量不会产生伪回归结果,并且这两个变量存在长期稳定的关系。
13.马尔科夫分析中,转移概率的概念;计算一步转移概率矩阵;马尔科夫的特点,无后效性,终极概率
转移概率:在事件的发展变化过程中,从某一状态出发,下一时刻转移到其他状态的可能性。
马尔科夫的特点
①无后效性(马尔科夫性):过程(或系统)在时刻t0所处的状态为已知的条件下,过程在时刻t>t0所处状态的条件分布与过程在时刻t0之前所处的状态无关的特性。即:过程“将来”的情况与“过去”的情况是无关的。
②终极概率:经过无穷多次状态转移后所得到的状态概率称为终极状态概率,或称平衡状态概率
14.相关分析中,什么是典型相关分析,含义
由于一组变量可以有无数种线性组合(线性组合由相应的系数确定),因此必须找到既有意义又可以确定的线性组合。
典型相关分析就是要找到这两组变量线性组合的系数,使得这两个由线性组合生成的变量(和其他线性组合相比)之间的相关系数最大。
15.统计特征中,偏度和峰度的概念,区别,联系
偏度系数:测度地理数据分布的不对称性情况,刻画以平均值为中心的偏向情况。
峰度系数:测度地理数据在均值附近的集中程度。
区别:偏度反映了数据的不对称性,峰度反映了数据的陡峭程度。
联系:两者都需要与正态分布进行比较。
16.时间序列中,截面数据和面板数据的概念,区别,联系
截面数据:又称横向数据,是一批发生在同一时间截面上的调查数据。
时间序列数据:又称为纵向数据,同一现象在不同时间上的相继观察值排列而成的数列。
面板数据:面板数据是时间序列数据与截面数据的合成体。
区别:面板数据是时间序列数据与截面数据的合成体。
联系:面板数据是时间序列数据与截面数据的合成体。
17.什么是计量地理学,研究对象,研究内容
计量地理学:是研究运用数学方法和计算机等现代技术手段,对地理现象、地理过程进行定量化研究,以揭示地理现象发生、发展的内在机制及演化规律,进行地理系统预测及优化调控的学科。
研究对象:①地理空间与过程的研究②人口、资源和环境的关系③区域优化与布局研究
研究内容:①空间要素分布②空间要素相互关系③空间要素过程④地理系统模拟、预测
18.半变异函数中各个参数的含义,并用示意图来表示,函数指标的意义
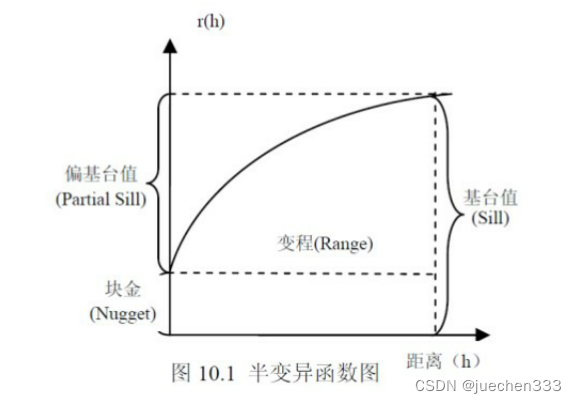
基台值:当变异函数随着间隔距离h的增大,从非零值达到一个相对稳定的常数时,该常数称为基台值C0+C,是系统或系统属性中最大的变异。
块金值(区域不连续性值):当间隔距离h=0时,变异函数等于C0,该值称为块金值或块金方差。
变程(空间依赖范围):变异函数达到基台值时的间隔距离a称为变程。变程表示在h≥a以后,区域化变量Z(x)空间相关性消失。
分维数:表示变异函数的特性,由变异函数和间隔距离h之间的关系确定。
19.聚类分析中,如何进行系统聚类;什么是模糊聚类,在哪些领域应用
系统聚类:开始时把每个样品作为一类,然后把最靠近的样品(即距离最小的群品)首先聚为小类,再将已聚合的小类按其类间距离再合并,不断继续下去,最后把一切子类都聚合到一个大类。
模糊聚类:模糊集理论的提出为软划分提供了有力的分析工具,用模糊数学的方法来处理聚类问题,被称之为模糊聚类分析。由于模糊聚类得到的样本属于各个类别的不确定性程度,表达了样本类属的中介性,更能客观地反映现实世界,从而成为聚类分析研究的主流。
应用:模式识别、图像处理、信道均衡、矢量量化编码、神经网络的训练、参数估计、医学诊断、天气预报、食品分类、水质分析等。
20.主成分分析过程中,特征值,特征向量,载荷之间的关系,写出主成分的表达式
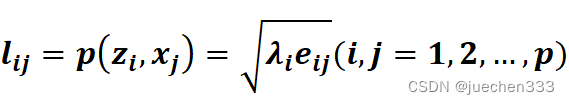
21.BP神经网络的定义,优缺点
BP神经网络是一种按误差反向传播(简称误差反传)训练的多层前馈网络,它的基本思想是梯度下降法,利用梯度搜索技术,以期使网络的实际输出值和期望输出值的误差均方差为最小。
优点:①非线性映射能力,②泛化能力,③容错能力
缺点:①容易形成局部极小值而得不到全局最优值,②训练次数多使得学习效率低,收敛速度慢,③隐含层的选取缺乏理论的指导,④训练时学习新样本有遗忘旧样本的趋势