参考文档:
《基于主从博弈的智能小区代理商定价策略及电动汽车充电管理》基本复现
仿真平台:
MATLAB+CPLEX/gurobi平台
优势:
代码具有一定的深度和创新性,注释清晰,非烂大街的代码,非常精品!
主要内容:
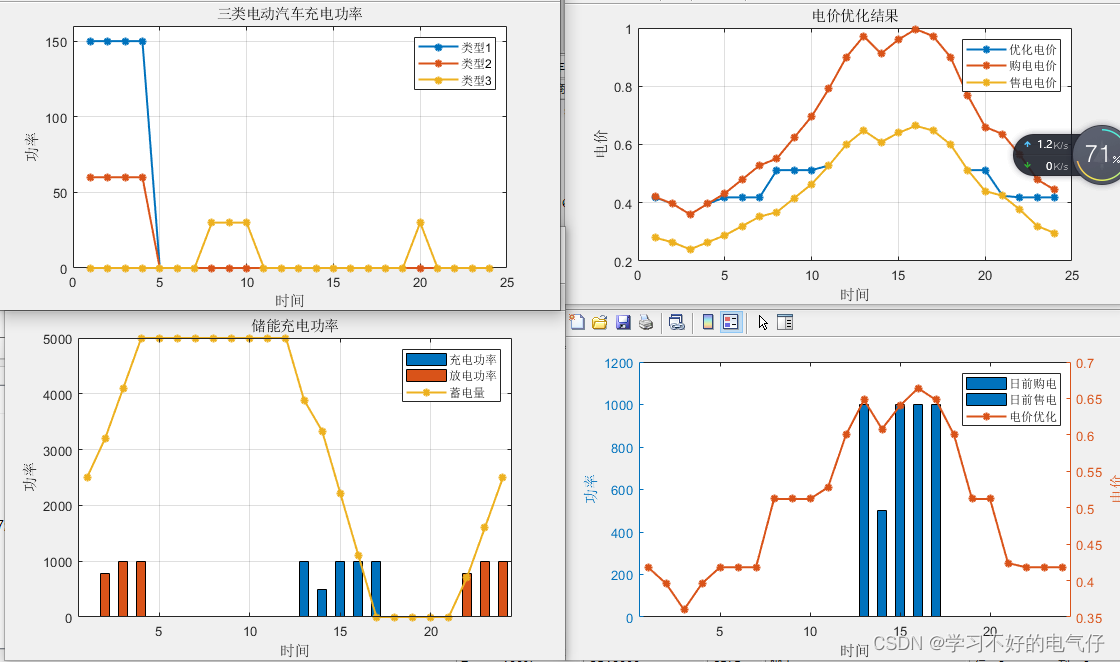
代码主要做的是一个电动汽车充电管理和智能小区代理商动态定价的问题,将代理商和车主各自追求利益最大化建模为主从博弈,上层以代理商的充电电价作为优化变量,下层以电动汽车的充电策略作为优化变量,通过优化得出最优电价策略以及动态充电策略,代码出图效果非常好。
部分代码:
clear
clc
%%%%主从博弈%%%
PL=[1733.66666666000;1857.50000000000;2105.16666657000;2352.83333343000;2476.66666657000;2724.33333343000;2848.16666657000;2972;3219.66666657000;3467.33333343000;3591.16666657000;3715.00000000000;3467.33333343000;3219.66666657000;2972;2600.50000000000;2476.66666657000;2724.33333343000;2972;3467.33333343000;3219.66666657000;2724.33333343000;2229;1981.33333343000];
a=0.55*PL/mean(PL);
b=0.55/mean(PL)*ones(24,1);;
%b=zeros(24,1);
lb=0.2;
ub=1;
T_1=[1;1;1;1;1;1;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;1;1;1];%%%早出晚归型
T_2=[1;1;1;1;1;1;1;1;0;0;0;0;1;1;1;0;0;0;0;1;1;1;1;1];%%%上班族
T_3=[0;0;0;0;0;0;0;1;1;1;1;1;1;1;1;1;1;1;1;1;0;0;0;0];%%%夜班型
Ce=sdpvar(24,1);%电价
Pb=sdpvar(24,1);%购电
Pc1=sdpvar(24,1);%一类车充电功率
Pc2=sdpvar(24,1);%二类车充电功率
Pc3=sdpvar(24,1);%三类车充电功率
C=[lb<=Ce<=ub,mean(Ce)==0.7,Pb>=0];%边界约束
C=[C,Pc1+Pc2+Pc3==Pb];%能量平衡
L_u=sdpvar(1,3);%电量需求等式约束的拉格朗日函数
L_lb=sdpvar(24,3);%充电功率下限约束的拉格朗日函数
L_ub=sdpvar(24,3);%充电功率上限约束的拉格朗日函数
L_T=sdpvar(24,3);%充电可用时间约束的拉格朗日函数
f=200*L_u(1)*(0.9*42-9.6)+150*L_u(2)*(0.9*42-9.6)+50*L_u(3)*(0.9*42-9.6)+sum(sum(L_ub).*[32*30,32*30,16*30])-sum(a.*Pb+b.*Pb.^2);%目标函数
C=[C,Ce-L_u(1)*ones(24,1)-L_lb(:,1)-L_ub(:,1)-L_T(:,1)==0,Ce-L_u(2)*ones(24,1)-L_lb(:,2)-L_ub(:,2)-L_T(:,2)==0,Ce-L_u(3)*ones(24,1)-L_lb(:,3)-L_ub(:,3)-L_T(:,3)==0];%KKT条件
C=[C,sum(Pc1)==200*(0.9*42-9.6),sum(Pc2)==150*(0.9*42-9.6),sum(Pc3)==50*(0.9*42-9.6)];%电量需求约束
for t=1:24
if T_1(t)==0
C=[C,Pc1(t)==0];
else
C=[C,L_T(t,1)==0];
end
if T_2(t)==0
C=[C,Pc2(t)==0];
else
C=[C,L_T(t,2)==0];
end
if T_3(t)==0
C=[C,Pc3(t)==0];
else
C=[C,L_T(t,3)==0];
end
end
运行结果: