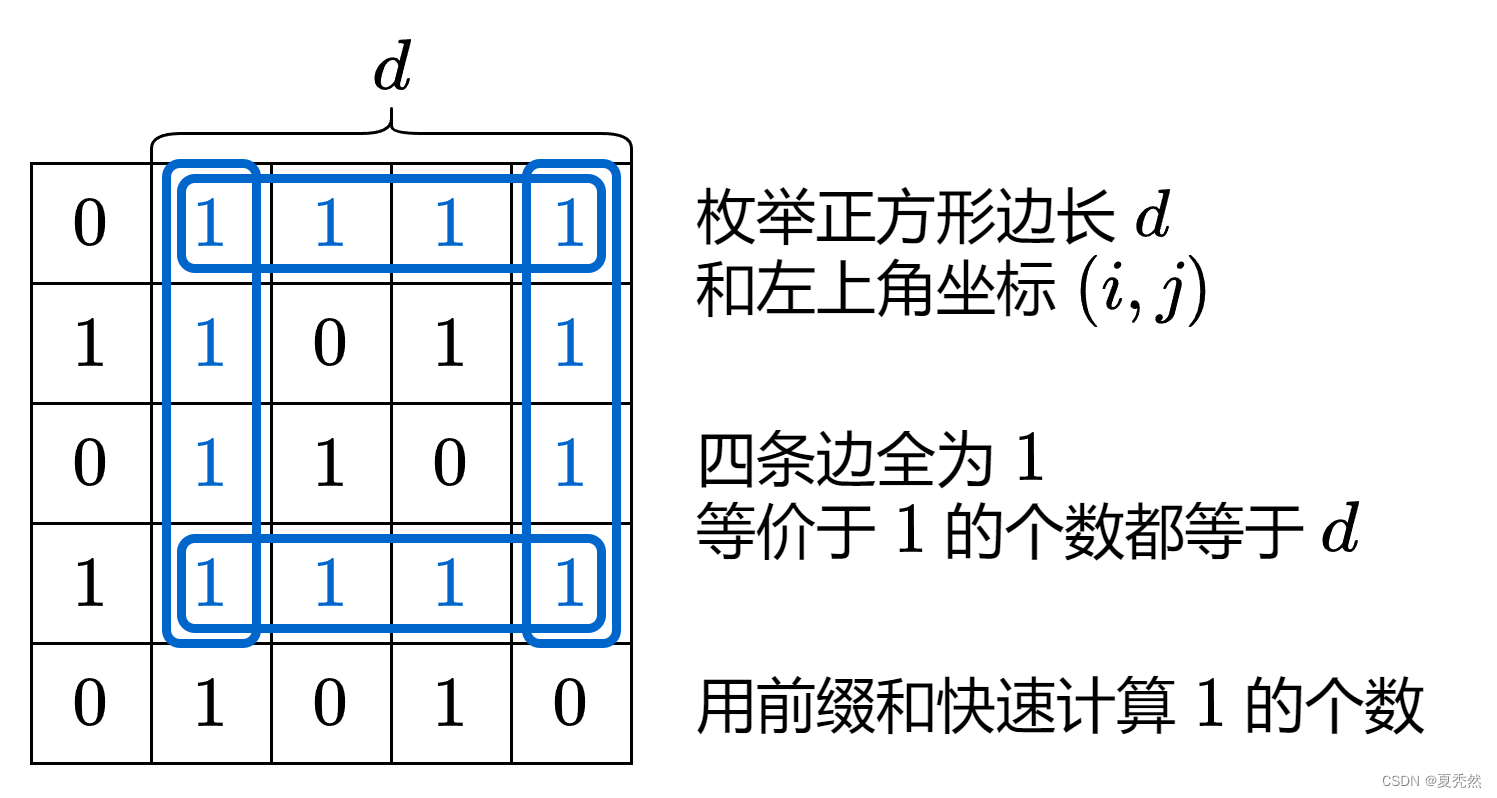
最大的以 1 为边界的正方形
难度:中等
给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。如果不存在,则返回 0。
示例 1:
输入:grid = [[1,1,1],[1,0,1],[1,1,1]]
输出:9
示例 2:
输入:grid = [[1,1,0,0]]
输出:1
前缀和
思路:
- 数据量较小,也可以用二维前缀和写,用前缀和节省边长的计算时间
- 遍历正方形边长求出区域和,然后减去中间那块区域是否等于两边都为
1
1
1的和,假如正方形边长为
3
3
3,那么边长都为
1
1
1的和为:
3
2
−
(
3
−
2
)
2
=
8
3^2-(3-2)^2=8
32−(3−2)2=8
复杂度分析:
- 时间复杂度: O ( m n ) O(mn) O(mn),其中 m m m 和 n n n 分别为 grid \textit{grid} grid 的行数和列数,不一定是 m n mn mn,大佬可是帮我分析一下是多少。
- 空间复杂度: O ( m n ) O(mn) O(mn)。
class Solution:
def largest1BorderedSquare(self, grid) -> int:
# 构建前缀和,行列各构建一个数组
row, col = len(grid), len(grid[0])
prev_row = [[0] * (col + 1) for _ in range(row)]
prev_col = [[0] * (row + 1) for _ in range(col)]
for i in range(row):
for j in range(col):
prev_row[i][j+1] = prev_row[i][j] + grid[i][j]
prev_col[j][i+1] = prev_col[j][i] + grid[i][j]
# 遍历所有元素
res = 0
for i in range(row):
for j in range(col):
# 如果该节点为1,则可能是正方形的左顶点
if grid[i][j] == 1:
# 令长度等于当前遍历过的最大长度
length = res
# 慢慢增加边长看是否能成立
while length + i <= row and length + j <= col:
# 如果长度不合适,那无论怎么增加长度,都不可能是正方形,直接退出
if prev_row[i][j + length] - prev_row[i][j] != length:
break
# 计算4条边的长度
fh = prev_row[i][j + length] - prev_row[i][j]
fl = prev_col[j][i + length] - prev_col[j][i]
lh = prev_row[i + length - 1][j + length] - prev_row[i + length - 1][j]
ll = prev_col[j + length - 1][i + length] - prev_col[j + length - 1][i]
# 判断边上的点是否等于边长为length的值,如果相等那他就是一个正方形
if length ** 2 - max(0, length - 2)**2 == fh + fl + lh + ll - 4:
res = max(res, length)
length += 1
# 因为边长为1的时候,他的边长不是 四条边分别的元素个数 - 4,而且只要有原始是1,
# 就说明是边长为1的正方向,所以每次出来的时候,让他和1取最大的边长为结果
if res < 1:
res = 1
return res ** 2
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/largest-1-bordered-square