目录
一.滑动窗口
1.什么滑动窗口
2.滑动窗口的三要素
二.找到字符串中所有字母异位词
1.题目描述
2.问题分析
3.代码实现
三.字符串的排列
1.题目描述
2.问题分析
3.代码实现
四.考试的最大困扰度
1.题目描述
2.问题分析
3.代码实现
五.替换后的最长重复字符
1.题目描述
2.问题分析
3.代码实现
六.尽可能使字符串相等
1.题目描述
2.问题分析
3.代码实现
七.每种字符至少取 K 个
1.题目描述
2.问题分析
3.代码实现
一.滑动窗口
1.什么滑动窗口
滑动窗口是通过双指针同向移动而解决的一类问题
经常用于数组或者字符串,求其满足条件的连续子序列或者子串,将原先需要嵌套循环问题,转换为单循环问题,降低时间复杂度
主要分为两大类,一种是长度固定的滑动窗口,一种是长度动态变化的滑动窗口
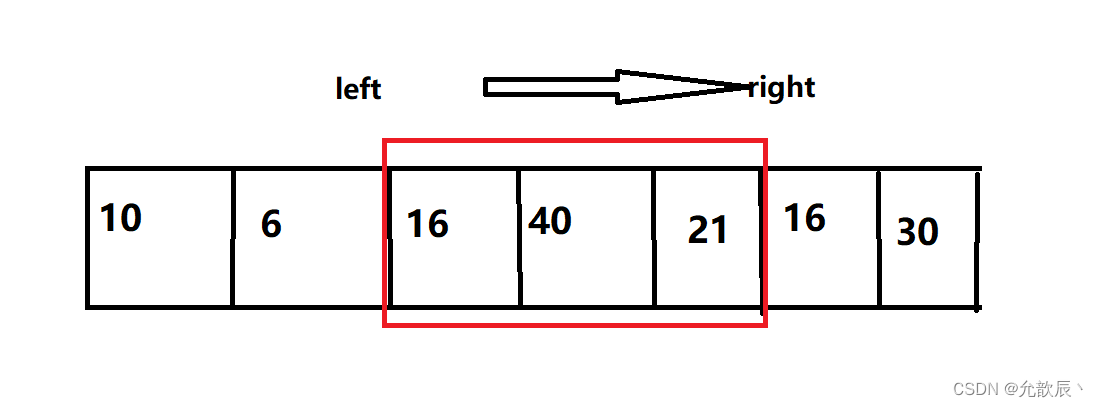
2.滑动窗口的三要素
我们分析问题主要就是考虑这三要素,寻找满足题意的条件,使窗口的右端(right)可以向右滑行,满足条件的时候,使窗口的左端(left)向右滑行,进行收缩,直到对整个数组(或字符串)线性遍历完成
窗口扩展是寻找可行解
窗口收缩是优化可行解
窗口只能从左至右滑动
注意:长度固定的滑动窗口不需要扩张和收缩,只需要保持固定的长度向右滑动即可
二.找到字符串中所有字母异位词
1.题目描述
给定两个字符串
s和p,找到s中所有p的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
力扣:力扣
2.问题分析
首先我们需要理解异位词,其实就是含有各个字母数量和一个子串的字母数量相同,那么就可以成为异位,例如(aab)和(baa),他们的长度也是相同的,所以只需要在字符串s中找到长度和p字符串长度相同且各个字母数量相同的字符串即可.这很容易可以想象到滑动窗口,并且长度固定为p的长度的窗口
这里我们采用一个长度为26的字符数组来统计长度为p长度的滑动窗口的字母数量,和p的字符数组进行比较,相同即可加入到list数组中
3.代码实现
public List<Integer> findAnagrams(String s, String p) {
ArrayList<Integer> list = new ArrayList<>();
if (p.length() > s.length())
return list;
int[] sCount = new int[26];
int[] pCount = new int[26];
for (int i = 0; i < p.length(); ++i) {
pCount[p.charAt(i) - 'a']++;
}
for (int i = 0; i < p.length() - 1; ++i) {
sCount[s.charAt(i)-'a']++;
}
for (int i = 0; i <= s.length() - p.length(); ++i) {
sCount[s.charAt(i + p.length() - 1)-'a']++;
if (Arrays.equals(sCount, pCount)) {
list.add(i);
}
sCount[s.charAt(i)-'a']--;
}
return list;
}三.字符串的排列
1.题目描述
给你两个字符串
s1和s2,写一个函数来判断s2是否包含s1的排列。如果是,返回true;否则,返回false。换句话说,
s1的排列之一是s2的 子串 。
力扣: 力扣
2.问题分析
这一题和上一题大致相似,自己可以来尝试一下,排列其实就是异位
3.代码实现
public boolean checkInclusion(String s1, String s2) {
if(s1.length()>s2.length())
return false;
char[] countS1 = new char[26];
char[] countS2 = new char[26];
for (int i = 0; i < s1.length(); ++i) {
countS1[s1.charAt(i) - 'a']++;
countS2[s2.charAt(i) - 'a']++;
}
if (Arrays.equals(countS1, countS2)) {
return true;
}
for (int i = s1.length(); i < s2.length(); ++i) {
countS2[s2.charAt(i - s1.length()) - 'a']--;
countS2[s2.charAt(i) - 'a']++;
if (Arrays.equals(countS1, countS2)) {
return true;
}
}
return false;
}四.考试的最大困扰度
1.题目描述
一位老师正在出一场由
n道判断题构成的考试,每道题的答案为 true (用'T'表示)或者 false (用'F'表示)。老师想增加学生对自己做出答案的不确定性,方法是 最大化 有 连续相同 结果的题数。(也就是连续出现 true 或者连续出现 false)。给你一个字符串
answerKey,其中answerKey[i]是第i个问题的正确结果。除此以外,还给你一个整数k,表示你能进行以下操作的最多次数:
- 每次操作中,将问题的正确答案改为
'T'或者'F'(也就是将answerKey[i]改为'T'或者'F')。请你返回在不超过
k次操作的情况下,最大 连续'T'或者'F'的数目。
力扣:力扣
2.问题分析
分析了问题可以知道,这一题包含了字符串,连续T或F字符最大的字眼,因此很容易想到需要使用滑动窗口,因为不确定最大连续字符串的长度,所以这一题的窗口长度是不固定的.问题其实可以分为以下两种情况:
第一种情况:使用k次机会将遇到的F变成T,在这种情况下使求得连续T的最大数目.
第二种情况:使用k次机会将遇到的T变成F,在这种情况下使求得连续F的最大数目.
最后只需要求得T和F连续的最大数目两者的最大值即可
分析窗口扩张的情况:(拿求连续T长度最大)因为有k次机会,所以当窗口中F数量小于等于k的时候,这个时候窗口的right向右滑行

分析窗口收缩的情况:当窗口中F的数量大于k的时候,这个时候窗口left进行收缩,直到k的数量小于等于k的时候

满足条件的窗口大小即为一个符合条件的连续T的长度,只需要寻找满足条件的窗口的最大值即可.
3.代码实现
public int maxConsecutiveAnswers(String answerKey, int k) {
return Math.max(maxCount(answerKey, k, 'T'), maxCount(answerKey, k, 'F'));
}
public int maxCount(String answerKey, int k, char c) {
int ans = 0;
for (int left = 0, right = 0, sum = 0; right < answerKey.length(); ++right) {
sum += answerKey.charAt(right) != c ? 1 : 0;
while (sum > k) {
sum -= answerKey.charAt(left) != c ? 1 : 0;
left++;
}
ans = Math.max(ans, right - left + 1);
}
return ans;
}五.替换后的最长重复字符
1.题目描述
给你一个字符串
s和一个整数k。你可以选择字符串中的任一字符,并将其更改为任何其他大写英文字符。该操作最多可执行k次。在执行上述操作后,返回包含相同字母的最长子字符串的长度。
力扣:力扣
2.问题分析
这一题和上一题基本类似,上一题只包含T和F两种字符,这一题一共26中字符(A--Z),所以要比较26次最大值,求出结果.
分析窗口扩张的情况:当窗口中不等于c字符的数量小于等于k次的时候,窗口右端right向右滑行
分析窗口收缩的情况:当窗口中不等于c字符的数量大于k次的时候,窗口左端left向右滑行,直到窗口中c字符的数量小于等于k次.
3.代码实现
public int characterReplacement(String s, int k) {
int res = 0;
HashSet<Character> set = new HashSet<>();
for (char c : s.toCharArray()) {
set.add(c);
}
for (Character character : set) {
res = Math.max(res, countMax(s, k, character));
}
return res;
}
public int countMax(String s, int k, char c) {
int res = 0;
for (int left = 0, right = 0, cnt = 0; right < s.length(); ++right) {
cnt += s.charAt(right) != c ? 1 : 0;
while (cnt > k) {
cnt -= s.charAt(left) != c ? 1 : 0;
left++;
}
res = Math.max(res, right - left + 1);
}
return res;
}做完这题可以自己去做下:1004. 最大连续1的个数 III: 力扣 1493. 删掉一个元素以后全为 1 的最长子数组:力扣
六.尽可能使字符串相等
1.题目描述
给你两个长度相同的字符串,
s和t。将
s中的第i个字符变到t中的第i个字符需要|s[i] - t[i]|的开销(开销可能为 0),也就是两个字符的 ASCII 码值的差的绝对值。用于变更字符串的最大预算是
maxCost。在转化字符串时,总开销应当小于等于该预算,这也意味着字符串的转化可能是不完全的。如果你可以将
s的子字符串转化为它在t中对应的子字符串,则返回可以转化的最大长度。如果
s中没有子字符串可以转化成t中对应的子字符串,则返回0。
力扣: 力扣
2.问题分析
这一题虽然和上一题不一样,但这一题更加简单,因为很容易想到窗口扩张和收缩的条件
分析窗口扩张的情况:当遍历到i位置的时候,所需要的预算小于等于maxCost的时候,窗口的右端可以继续向右滑行
分析窗口收缩的情况:当遍历到i位置的时候,所需要的预算大于maxCost的时候,窗口的右端不可以继续向右滑行,这个时候窗口左端left收缩,直到小于maxCost
3.代码实现
public int equalSubstring(String s, String t, int maxCost) {
int res = 0;
for (int left = 0, right = 0, sum = 0; right < s.length(); ++right) {
sum += Math.abs(t.charAt(right) - s.charAt(right));
while (sum > maxCost) {
sum -= Math.abs(t.charAt(left) - s.charAt(left));
left++;
}
res = Math.max(res, right - left + 1);
}
return res;
}七.每种字符至少取 K 个
1.题目描述
给你一个由字符
'a'、'b'、'c'组成的字符串s和一个非负整数k。每分钟,你可以选择取走s最左侧 还是 最右侧 的那个字符。你必须取走每种字符 至少
k个,返回需要的 最少 分钟数;如果无法取到,则返回-1。
力扣:力扣
2.问题分析
正难则反,我们不妨换一个角度考虑一下问题,问题是我们每次从左端或右端取走字符,最终使取走各k个字符'a','b','c',那么我们不妨这样考虑:取走k个字符'a','b','c',字符串中还剩下多少个字符'a','b','c',求出长度最大的含有这样的子串,最终最小的分钟等于字符串的长度减去这个子串
设子串中要剩余至多cntA个'a',cntB个'b',cntC个'c'
分析窗口扩张的情况:当子串(滑动窗口)中所有字母的数量小于等于所需的数量(cntA,cntB,cntC)时候,窗口的right端向右滑行
分析窗口收缩的情况:当子串(滑动窗口)中任一个字母的数量大于所需的数量(cntA,cntB,cntC)时候,窗口的left端向左滑行,直至不符合条件
每次需要收集满足条件的窗口的长度,寻找到最大长度的窗口,最终的答案就是字符串的长度减去滑动窗口长度的最大值
3.代码实现
public int takeCharacters(String s, int k) {
int left = 0, right = 0, length = s.length();
char[] arr = s.toCharArray();
int max = 0;
int[] cnt = new int[3];//统计a,b,c的数量
for (int i = 0; i < length; ++i) {
cnt[arr[i] - 'a']++;
}
int cntA = cnt[0] - k, cntB = cnt[1] - k, cntC = cnt[2] - k;//分别为a,b,c可以剩下的最大数量
if (cntA == 0 && cntB == 0 && cntC == 0)//此时要全部取走
return length;
if (cntA < 0 || cntB < 0 || cntC < 0)//剩下的数量为负的时候,说明a,b,c的数量不足k个
return -1;
cnt = new int[3];//每次循环统计剩下的a,b,c的数量
while (right < length) {
cnt[arr[right] - 'a']++;
while (cnt[0] > cntA || cnt[1] > cntB || cnt[2] > cntC) {
cnt[arr[left] - 'a']--;
left++;//当剩下的字符串过长而不满足条件的时候,滑动窗口左端向右移
}
max = Math.max(max, right - left+1);
right++;//窗口的左端向右移
}
return length - max;
}