1.注意力机制

意义：人类的注意力机制极大提高了信息处理的效率和准确性。

公式：

 1)自注意力机制

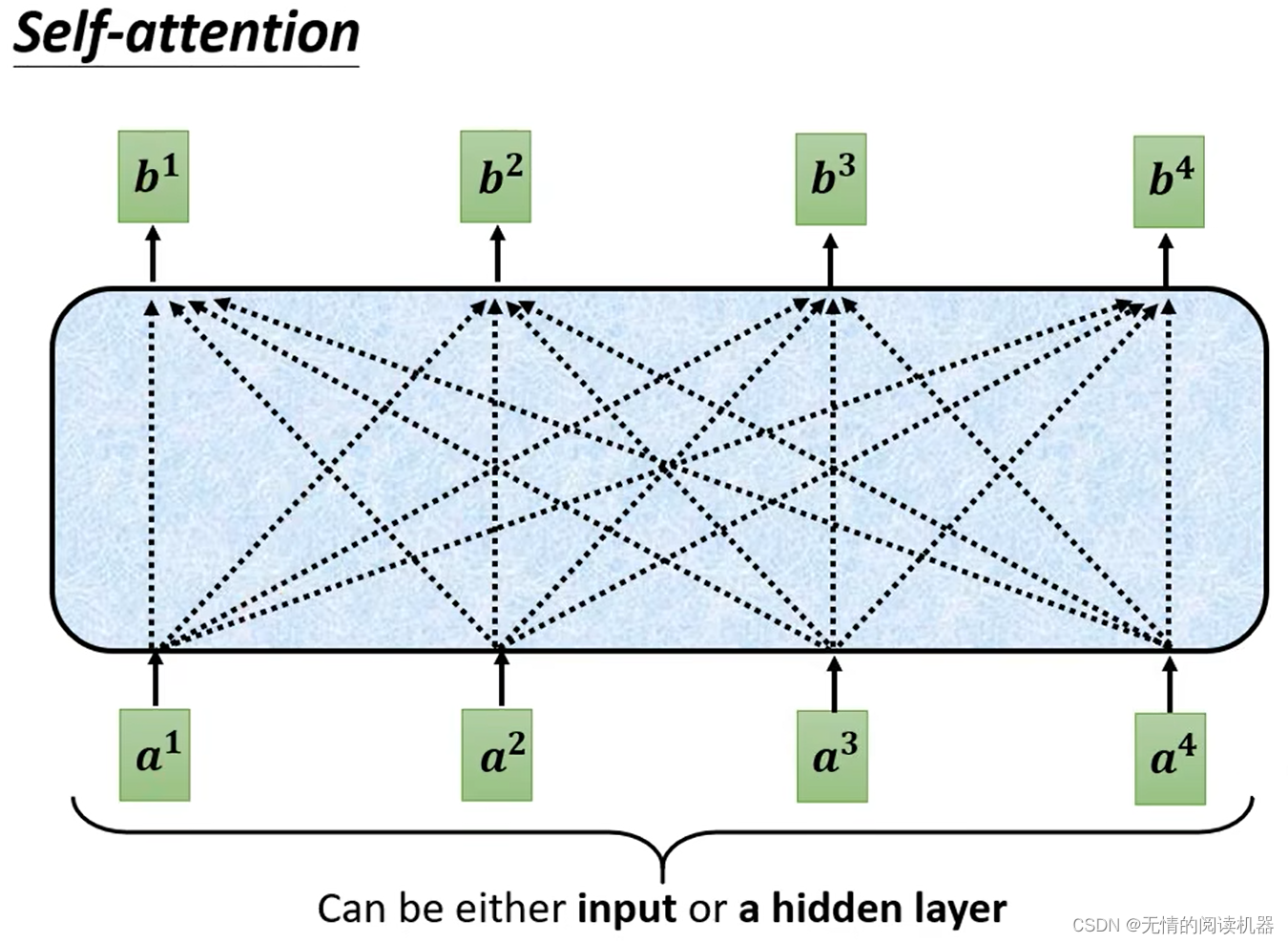
 b都是在考虑了所有a的情况下生成的。

以产生b1向量为例：

1.在a这个序列中，找到与a1相关的其他向量

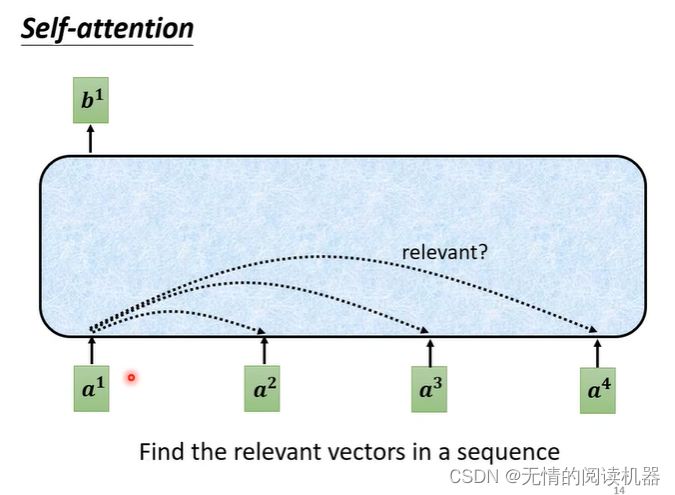
 2.每个向量与a1关联的程度，我们用数值α表示

那么这个数值如何计算的呢？

计算的方式有很多种：

我的理解：关联程度就相当于question（问题）与key(答案）的匹配程度

 

自己跟自己的关联也很重要 

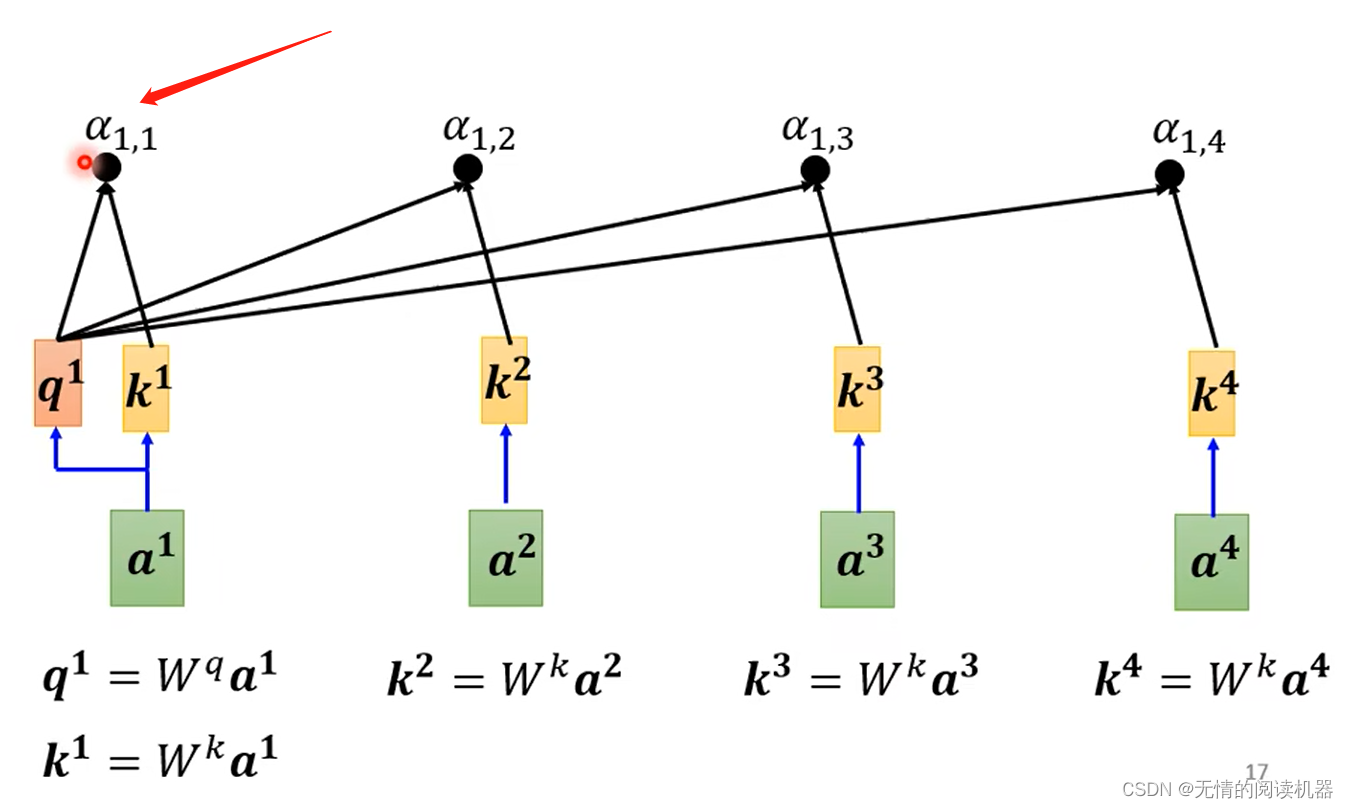
 然后将这些关联度放到softmax里面，得到最终的关联度

 最终乘v，得到最后的值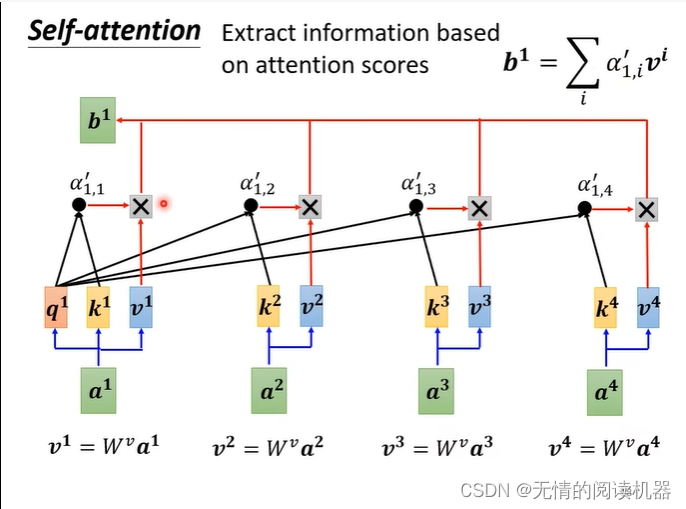

 上述是宏观的理解，现在从矩阵乘法再来看一遍

 

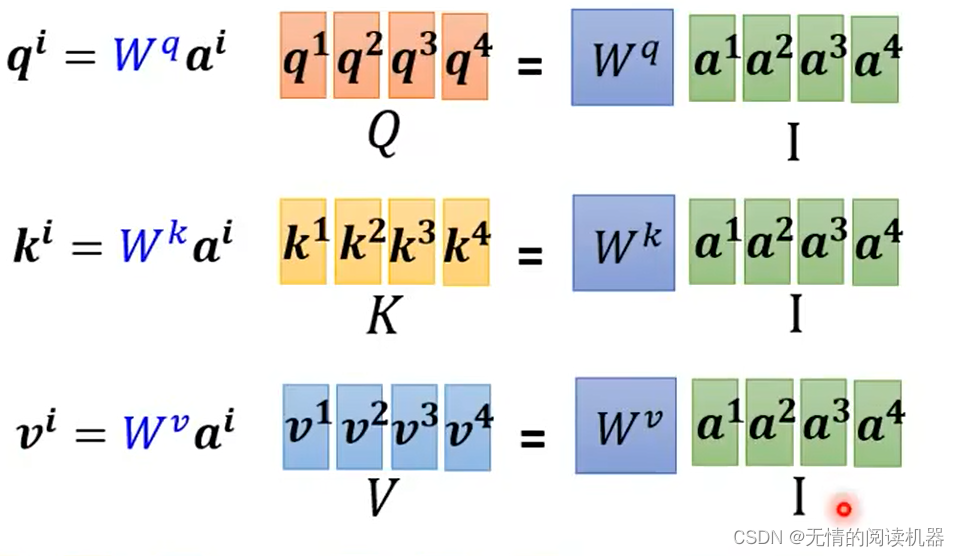
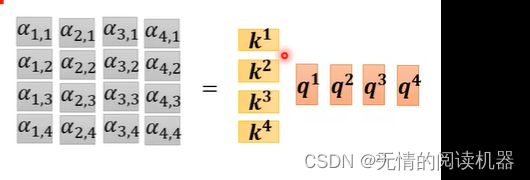
 整个过程只有三个w矩阵需要学习

 2）多头自注意力

头1只跟头1计算，头2只跟头2计算，头n只跟头n计算。

 

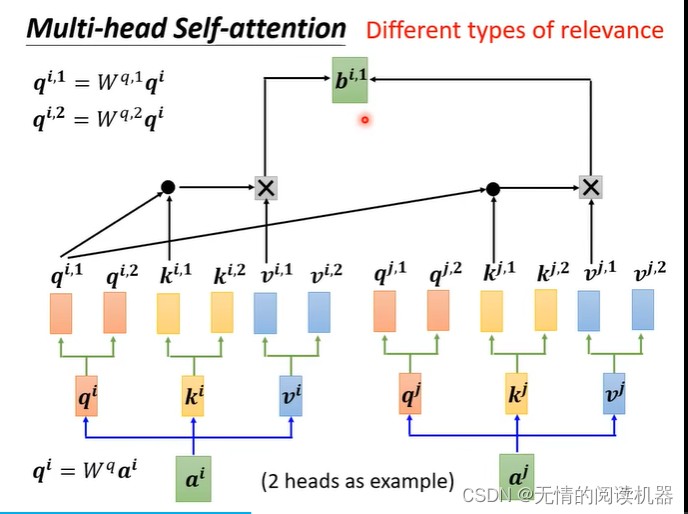
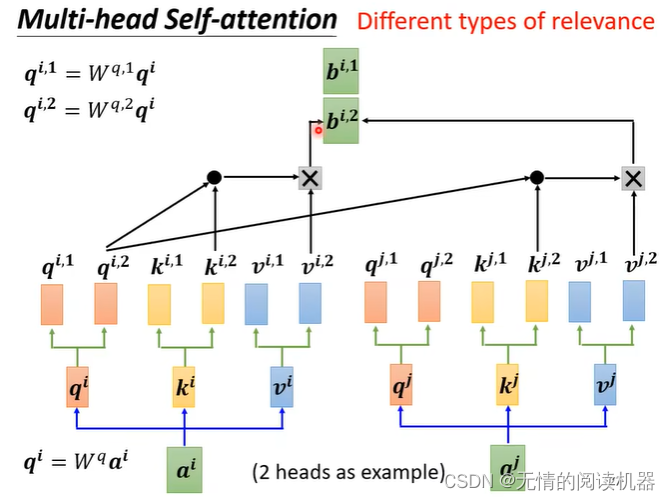
乘上一个矩阵，得到最终的bi，传入下一层 

 

Multi-head Attention 的本质是，在参数总量保持不变的情况下，将同样的 Query，Key，Value 映射到原来的高维空间的不同子空间中进行 Attention 的计算，在最后一步再合并不同子空间中的 Attention 信息。这样降低了计算每个 head 的 Attention 时每个向量的维度，在某种意义上防止了过拟合；由于 Attention 在不同子空间中有不同的分布，Multi-head Attention 实际上是寻找了序列之间不同角度的关联关系，并在最后拼接这一步骤中，将不同子空间中捕获到的关联关系再综合起来。

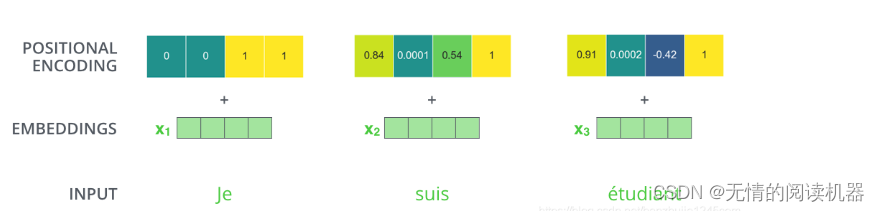
 3)位置信息

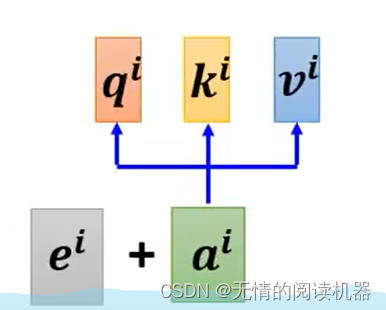
 有了位置信息的加持，a向量才算的上是有顺序的。

3）注意力机制

意义：可以从众多信息中，得到对解决问题最有用的信息。节省了算力资源，提高模型效率和能力。

比如看黑板学习知识，边边角角的部分是无效信息，老师敲黑板的地方是要关注的有效信息。

 

x1就是tom ，x2就是chase ，x3就是jerry ，先编码再解码得到y1汤姆，y2追逐 ，y3杰瑞

如果我们采用分心模型，计算过程是这样的。这样的重要程度是也一样的。

 

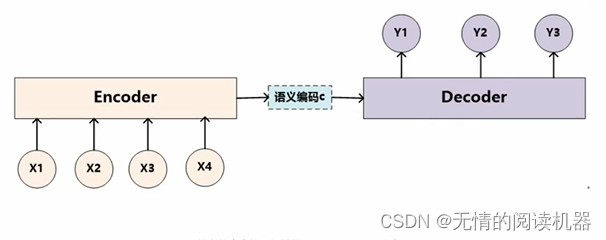
 encoder-decoder框架

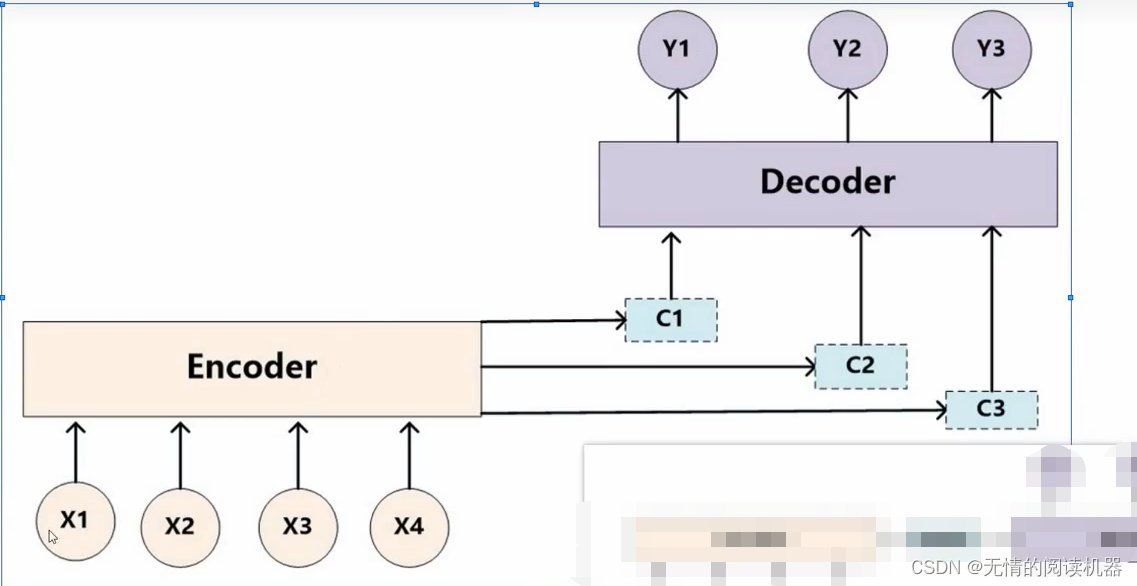
 所以加深一下attention的概念：

 

 计算过程与自注意力相似

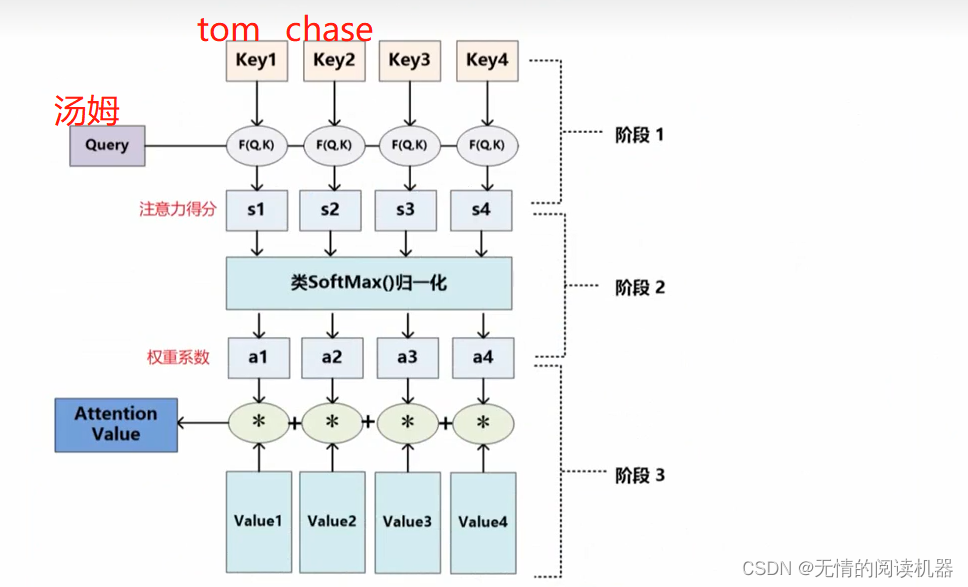
其中F(Q,K)是计算相似性的方法，并且方法不唯一

 

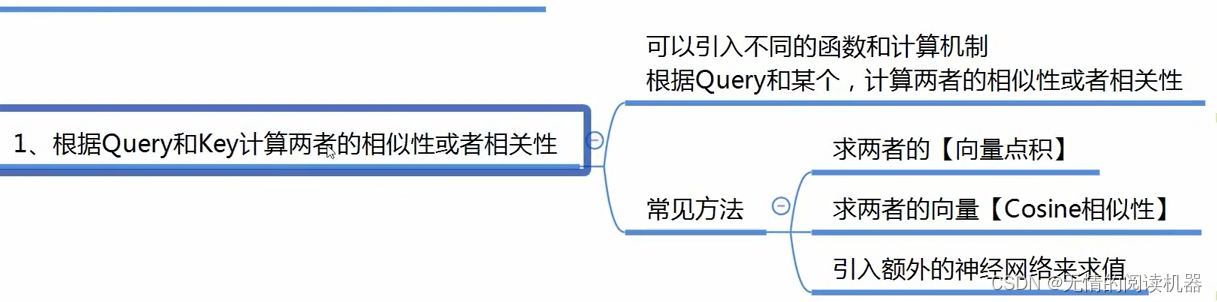
 2.transformer

1)结构

 

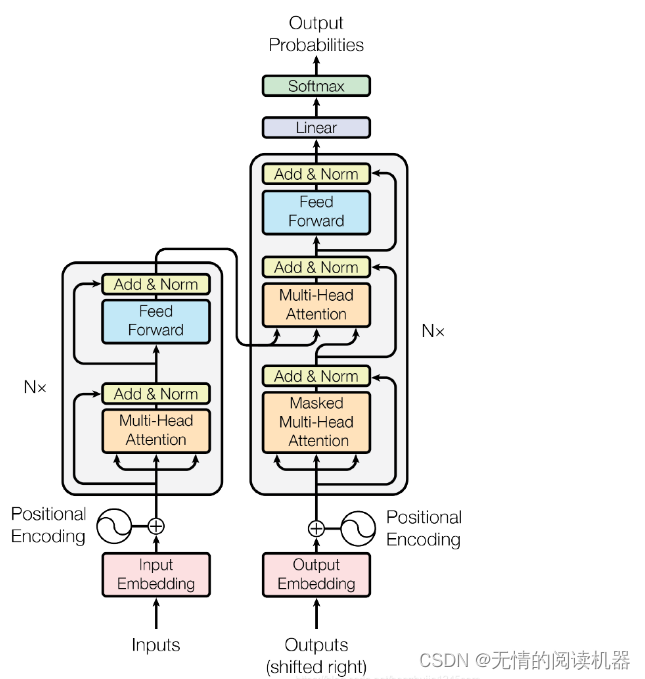
 Transformer 本质上是一个 Encoder-Decoder 架构。因此中间部分的 Transformer 可以分为两个部分：编码组件和解码组件

 论文中编码器和解码器使用了六层

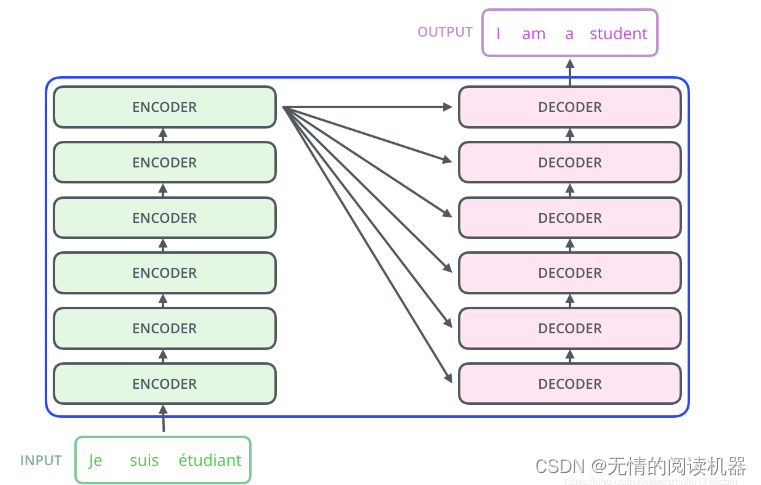
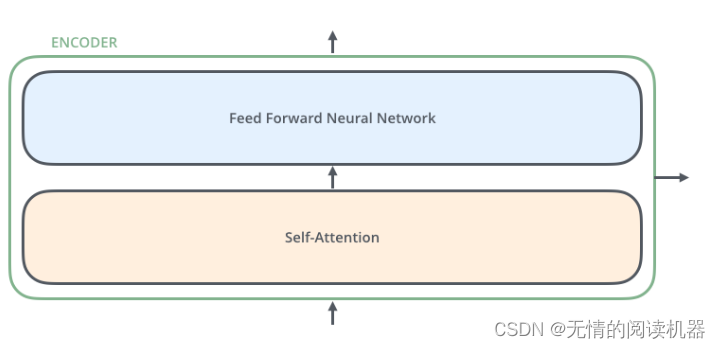
 每个编码器由两个子层组成：Self-Attention 层（自注意力层）和 Position-wise Feed Forward Network（前馈网络，缩写为 FFN）。每个编码器的结构都是相同的，但是它们使用不同的权重参数。位置前馈网络就是一个全连接前馈网络，每个位置的词都单独经过这个完全相同的前馈神经网络。其由两个线性变换组成，即两个全连接层组成，第一个全连接层的激活函数为 ReLU 激活函数。

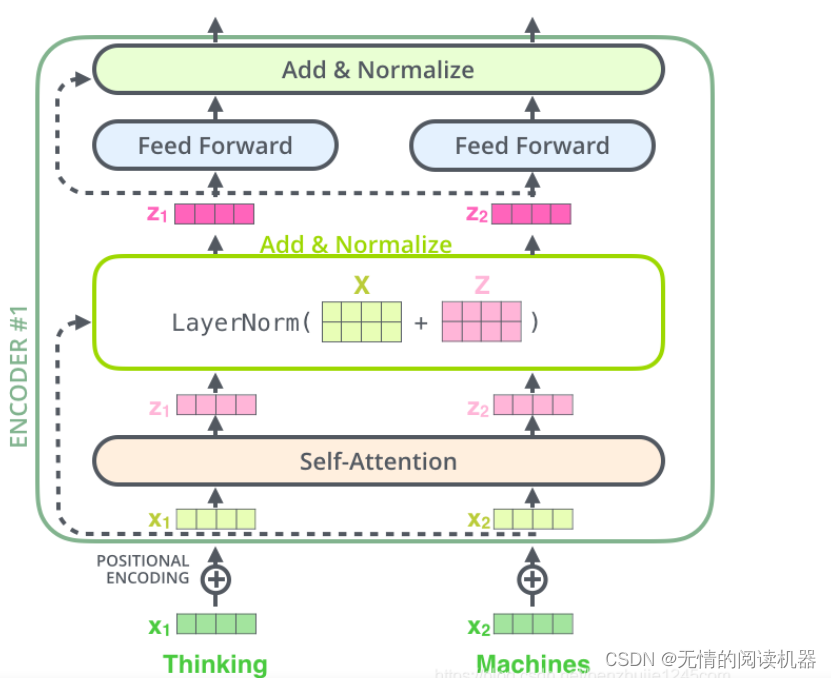
 每个编码器的每个子层（Self-Attention 层和 FFN 层）都有一个残差连接，再执行一个层标准化操作，整个计算过程可以表示为：

 2）位置编码

再提一嘴位置编码