1. 线性表

具有1:1的线性关系的数据对象称为线性表。

1.1 线性表的定义

线性表是最简单的一种线性结构，具有如下特征。
（1）线性表中必存在唯一的一个“第一元素”。
（2）线性表中必须存在唯一的一个“最后元素”。
（3）除了最后元素之外，其余元素均有唯一的直接后继。
（4）除了第一个元素之外，其余元素均有唯一的直接前驱。

线性表的抽象数据类型定义形式：

ADT List
{ 数据对象：
D={ai | ai∈ElemSet,i=1,2,…,n>=0}
{ n为线性表的表长，即数据元素的个数；n=0时的线性表为空表。}
数据关系：
R ={ <ai-1,ai> |ai-1,ai∈D, i=2,3,…,n }
{ 设线性表为(a1,a2,…,ai,…,an),称i为ai在线性表中的位序}
基础操作：
初始化操作
销毁操作
访问型操作
加工型操作
} ADT List

&L表示会引起线表的变化，L表示不会引起线标的变化。

下面分别介绍线性表的各个基本操作的初始条件和实现的功能

1.1.1 访问型操作

这类操作只是访问线性表中的元素，并没有改变线性表。
（1）判断线性表是否为空：ListEmpty（L）。
初始条件：线性表L存在。
操作结果：若L为空表，则返回TRUE，否则返回FALSE。
（2）求线性表的长度：ListLength（L）
初始条件：线性表存在。
操作结果：放回L中的数据元素的个数。
（3）得到线性表中某个位置上的元素：GetElem（L，i，&e）。
初始化条件：线性表L已存在，且 1<=i<=LengthList（L）。
操作结果：用e返回L中第i个元素的值。
（4）通知比较，寻找位置：LocateElem（L，e，compare（））。
初始条件：线性表L已存在，e为给定值，compare（）是元素比较函数。
操作条件：返回L中第1个与e满足关系compare（）的元素的位序。若这样的元素不存在，则返回值-1 。
（5）遍历线性表：ListTraverse（L）。
初始条件：线性表L已存在。
操作结果：依次访问L中的每个元素。

1.1.2 加工型操作

这类操作改变了原有的线性表。
（1）初始化操作：InitList（&L）。
操作结果：构造一个空的线性表L。
（2）销毁操作：DestroyList（&L）。
初始条件：线性表L已存在。
操作结果：销毁线性表L。
（3）线性表置空：CleaerList（&L）。
初始化条件：线性表L已存在。
操作结果：将L重置为空表，L由非空为空。
（4）修改线性表中某个位置上的元素置：PutElem（&L，i，e）。
初始化条件：线性表L已存在，且1<=i<=LengthList（L）。
操作结果：给L中第i个元素赋值e。L中的第i个元素的值发生了改变。
（5）在第i个位置上插入数据元素：ListInsert（&L，i，e）。
初始条件：线性表L已存在，且1<=i<=LengthList（L）+1.
操作结果：在L的第i个元素之前插入新的元素e，并将L的长度增1 。
（6）将线性表的第i个元素删除：ListDelete（&L，i，e）。
初始条件：线性表L已存在，且1<=i<=LengthList（L）。
操作结果：删除L的第i个元素，并且用e 返回其值，同时将L的长度减1 。

其中最重要的是插入操作和删除操作。

1.2 线性表的顺序存储结构

线性表的顺序存储结构是用一组连续的存储空间存放线性表中的各个数据元素，并用位置相邻的存储空间关系表示线性表中数据元素的直接前驱和直接后继的次序关系，称为顺序表。

1.2.1 定义顺序表数据类型方法1

包括以下数据成员：
（1）一片连续的存储空间（数组用于存放数据元素）。
（2）线性表的容量（数组的大小防止溢出）。
（3）线性表的长度（已经存入到数组中的数据元素个数）。

1.2.2 定义顺序表数据类型方法2

包括以下数据成员：
（1）一片连续的存储空间的起始地址（存放数组的起始地址）。
（2）线性表的容量（数组的大小防止溢出）。
（3）线性表的长度（已经存入到数组中的数据元素个数）。

对于两种存储结构的不同描述。第一种容易理解，使用相对简单，但是数组是顺序表的成员，大小固定，因此缺乏灵活性。第二种理解起来有一定难度，数组不是顺序表的成员，可根据实际问题的需要吗，在初始化操作中自定义数组的大小，因此具有较好的灵活性。

1.3 顺序表的基本操作实现

为了使数据结构中的操作具有很好的健壮性，在函数的定义中，通常用函数值表示操作的成功与失败。函数值为1，表示成功；函数值为0，表示失败。有时候为了方便起见，也可以将操作的结果作为函数的返回值。

1.3.1 顺序表的初始化操作

顺序表的初始化操作是完成一片连续空间的申请，将空间的起始地址、容量大小和数据个数0依次存放到顺序表中对应成员中。
算法的实现：

int initSqList(SqList* L, int max)
{
	L->data = (STD*)malloc(max * sizeof(STD));
	if (L->data == NULL)
	{
		perror("initSqList::");
		exit(0);
	}
	L->length = 0;
	L->listSize = max;
	return 1;//表示初始化操作成功
}

函数exit（0）的功能是结束程序的执行。为什么当动态申请存储空间失败时不用“return 0；”，而是调用函数exit（0）？原因是既然顺序表的初始化失败了，其他的有关对顺序表的操作都不可能正确执行，因此退出程序，并放回到系统。
【算法分析】
该算法不涉及基本操作的循环执行，算法的时间复杂度为T(n) = O（1）。

1.3.2 顺序表的插入操作

顺序表的插入操作是将某个学生数据插入顺序表中指针成员指向数组的给定位置，并将顺序表的长度成员加1
算法实现如下：

int insertSqList(SqList* L, int i, STD x)//i是插入位置，对应下标是i-1
{
	//插入失败的情况判断
	if (i<1 || i>L->length + 1)
	{
		printf("插入位置异常！\n");
		return 0;
	}
	if (L->length >= L->listSize)
	{
		printf("容量不够！\n");
		return 0;
	}
	//将区间[i-1,L->lenght-1]内的一组数据元素向后移动一个位置
	for (int k = L->length - 1; k >= i - 1; k--)
	{
		L->data[k + 1] = L->data[k];
	}
	//将待插入数据放入指定位置i，即下标i-1上
	L->data[i - 1] = x;
	//长度加1
	L->length++;
	//插入成功
	return 1;
}

寻找插入位置，将数据插进来，需移动数据元素。
最好情况（i=n+1）;基本语句执行0次，时间复杂度为O（1）；
最坏情况（i=1）；基本语句执行n次，时间复杂度为O(n)；
平均情况（1<=i<=n+1）:等概率pi =1/(n+1)。

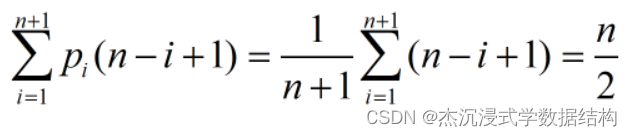
算法的时间复杂度为T(n)=O(n) 。

1.3.3 顺序表的删除操作

顺序表的删除操作是将顺序表中指针成员指向数组的给定位置的数组元素删除，并将数据个数减1.
算法实现如下：

int deleteSqList(SqList* L, int i, STD* x)
//i表示接受删除数据元素位置的整形变量
//x是将被删除的数据元素存回到主调函数中某个变量的指针变量
{
	//判断删除失败的条件是否成立
	if (L->length == 0)
	{
		printf("没有数据，不能删除！\n");
		return 0;
	}
	if (i <= 0 || i > L->length)
	{
		printf("位置异常，不能被删除\n");
		return 0;
	}
	//将被删除的数据元素存放到*x中
	*x = L->data[i - 1];
	//将区间[i,L->length-1]内的一组数据元素向前移动一个位置
	for (int k = i; k < L->length; k++)
	{
		L->data[k - 1] = L->data[k];
	}
	//长度减1
	L->length--;
	//删除成功
	return 1;
}

【算法分析】
寻找删除位置，将数据删除，需移动数据元素。
最好情况（i=n+1）;基本语句执行0次，时间复杂度为O（1）；
最坏情况（i=1）；基本语句执行n次，时间复杂度为O(n)；
平均情况（1<=i<=n）:等概率pi =1/(n)。

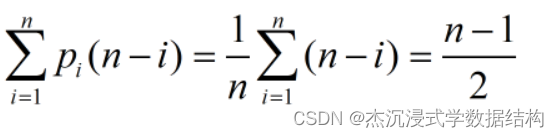
算法的时间复杂度为T(n)=O(n) 。

1.3.4 顺序表的更新操作

顺序表的更新操作是用新数据替换指定位置的数据。

int updateSqList(SqList* L, int i, STD x)
{
	//更新失败条件的判断
	if (L->length == 0)
	{
		printf("没有数据，不能更新！\n");
		return 0;
	}
	if (i<1 || i>L->length)
	{
		printf("位置不合适！\n");
		return 0;
	}
	//开始更新数据
	L->data[i - 1] = x;
	//更新成功
	return 1;
}

【算法分析】
该算法的操作不涉及循环，均为顺序执行，所以算法的时间复杂度为T(n)=O(1)。

1.3.5 顺序表的定位操作

顺序表的定位操作是根据给定的条件得到某个数据元素的位置。定位操作又称为查找操作。
位置从1开始
算法实现如下：

int locationSqList(SqList* L, char* newid)
{
	int i;
	//查找失败的条件判断
	if (L->length == 0)
	{
		printf("没有数据！\n");
		return 0;
	}
	for (int i = 0; i < L->length; i++)
	{
		//查找成功的条件的判断
		if (strcmp(L->data[i].name, newid) == 0)
		{
			return i + 1;
		}
	}
	//查找失败
	return 0;
}

【算法分析】
按照给定的条件，查找相应的数据元素，需逐个判断。最好的情况是O(1)；最坏的情况是O(n)。
等概率加权平均是O(n)。

1.3.6 顺序表的遍历操作

顺序表的遍历操作是输出顺序表中存放的所有数据元素。
分析：遍历操作不会引起顺序表的变化，遍历函数只需一个形参
算法实现如下：

int dispSqlist(SqList* L)
{
	if (L->length == 0)
	{
		printf("没有数据！\n");
		return 0;
	}
	for (int i = 0; i < L->length; i++)
	{
		printf("%10s%7.2f\n", L->data[i].name, L->data[i].score);
	}
	return 1;
}

【算法分析】
显示所有的数据，必须逐个依序显示，时间复杂度为T(n)=O(n)。

1.3.7 顺序表的创建操作

顺序表的创建操作依序存入顺序表中。
一共有两种算法：
算法1：调用初始化函数和插入函数创建顺序表

void createSqList1(SqList* L, int maxsize)
{
	int n = 0;
	STD x;
	char yn;

	//调用初始化函数，创建空表——申请空间来存储表的数据
	do
	{
		printf("请输入第%d个学生的姓名和分数，用空格隔开：", n + 1);
		scanf("%s%f", x.name, &x.score);
		//空度回车，以便下次正确读入数据
		getchar();
		//调用插入函数，将数据插入到尾部
		insertSqList(L, ++n, x);

		printf("继续输入吗？Y/N\n");
		scanf("%c", &yn);
	} while (yn == 'Y' || yn == 'y');
}

算法2：直接读取数据来创建顺序表

void createSqList2(SqList* L, int maxsize)
{
	int n=0;
	STD x;
	char yn;

	//初始化
	L->data = (STD*)malloc(maxsize * sizeof(STD));
	if (L->data == NULL)
	{
		perror("createSqList2::");
		return 0;
	}
	L->listSize = maxsize;
	L->length = 0;

	//读取数据并插入
	do
	{
		printf("请输入第%d个学生的姓名和分数，用空格隔开：", n + 1);
		scanf("%s%f", x.name, &x.score);
		//空度回车，以便下次正确读入数据
		getchar();
		L->data[n] = x;
		if (n >= L->listSize - 1)
		{
			break;
		}
		else
		{
			n++;
		}
		printf("继续输入吗？\n");
		scanf("%c", &yn);
	} while (yn == 'Y' || yn == 'y');
}