目录

题目

Input Specification:

Output Specification:

Sample Input:

Sample Output:

思路

C++ 知识UP

代码

---

题目

This is a problem given in the Graduate Entrance Exam in 2018: Which of the following is NOT a topological order obtained from the given directed graph? Now you are supposed to write a program to test each of the options.

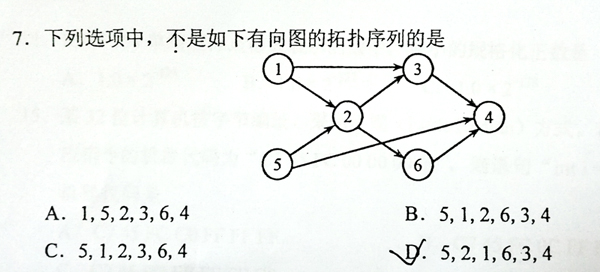
Input Specification:

Each input file contains one test case. For each case, the first line gives two positive integers N (≤ 1,000), the number of vertices in the graph, and M (≤ 10,000), the number of directed edges. Then M lines follow, each gives the start and the end vertices of an edge. The vertices are numbered from 1 to N. After the graph, there is another positive integer K (≤ 100). Then K lines of query follow, each gives a permutation of all the vertices. All the numbers in a line are separated by a space.

Output Specification:

Print in a line all the indices of queries which correspond to "NOT a topological order". The indices start from zero. All the numbers are separated by a space, and there must no extra space at the beginning or the end of the line. It is graranteed that there is at least one answer.

Sample Input:

6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
6
5 2 3 6 4 1
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6

Sample Output:

0 4 5

思路

难度评级：⭐️

1. 用邻接表存储图时，所用的空间和时间都会比较少；

        邻接表可以用vector<int> list[n]的形式；

2. 判断一个序列是否是拓扑序列时，只需要判断序列中每一个顶点在当时情况下的入度是否为0，为0后，则需要将其所指向的结点的入度都-1，重复该步骤；

3. 所以顶点的入度是比较常用的性质，应该用数组去存储，这样就可以避免每次都去遍历邻接表了，节省了时间

4. "a topological order"是拓扑序列的意思

C++ 知识UP

1. 一维数组的拷贝

一维数组可以直接拷贝到一个vector类型的容器中，方法如下：

vector<int> vec(arr, arr+n);// arr是一维数组，n是arr元素个数

也可以拷贝进另一个一维数组，方法如下：

copy(begin(arr), end(arr), begin(arrCopy)); 

2. 二维数组的拷贝

copy(&arr[0][0], &arr[0][0] + m * n, &arrCopy[0][0]); 

代码

#include <iostream>
#include <vector>

using namespace std;

int main(int argc, char** argv) {
	int n,m;
	cin>>n>>m;
	
	int in[1001]={0};// 统计各个顶点的入度 
	vector<int> list[1001];// 邻接表记录图结构 
	for(int i=0;i<m;i++) {
		int a,b;
		cin>>a>>b;
		list[a].push_back(b);
		in[b]++;
	}
	
	int K;
	cin>>K;
	
	bool flagOfSpace=false;
	for(int i=0;i<K;i++) {
		vector<int> order(n);
		for(int j=0;j<n;j++) cin>>order[j];
		
		vector<int> tin(in,in+n+1);
		// 检查每个顶点
		bool flagOfOrder=true;
		for(int j=0;j<n;j++) {
			int v=order[j]; 
			// 检查顶点v的入度是否为0
			if(tin[v]!=0) {
				flagOfOrder=false;
				break; 
			} 
			// 从v出发指向的顶点的入度统统-1
			for(int x:list[v]) {
				tin[x]--;
			} 
		}
		
		if(!flagOfOrder) {
			if(flagOfSpace) cout<<" ";
			flagOfSpace=true;
			cout<<i;
		}
	}
	return 0;
}