一、概念

1.1基础概念

灵敏度分析是一种分析模型输出响应程度与模型输入参数变化之间关系的方法，通过对模型输入参数进行变化和分析，来评估模型输出结果的稳定性和可靠性，以及各个输入参数对输出结果的影响程度。

1.2常用模型

1.3基本流程

1.4注意事项

二、基于python的灵敏度分析

2.1问题

在这个示例代码中，我们加载了一个包含股票价格和三个影响因素的数据集。然后，我们定义了一个线性回归模型，并对模型中的三个输入参数进行敏感性分析。我们使用SALib包中的saltelli函数生成1000个样本，然后运行模型并计算输出结果。最后，使用SALib包中的sobol函数对参数进行敏感性分析，并输出结果。

需要注意的是，这只是一个简单的示例，您可以根据自己的需要更改模型和参数设置，以实现更复杂的敏感性分析。在进行敏感性分析时，还需要仔细考虑模型的可靠性和准确性，以及数据质量的影响。

2.2步骤

2.2.1所用库的介绍

import pandas as pd
from sklearn.linear_model import LinearRegression
from SALib.sample import saltelli
from SALib.analyze import sobol
import numpy as np

skfuzzy是一个Python库，用于模糊逻辑系统的开发。它提供了一组函数和工具，可以帮助您在Python中构建和分析模糊系统。

首先导入了需要的包和库，包括pandas（用于数据处理）、sklearn.linear_model.LinearRegression（用于构建线性回归模型）、SALib.sample.saltelli（用于生成样本）、SALib.analyze.sobol（用于敏感性分析）、numpy（用于数据处理）等。

2.2.2加载数据

# 加载数据
f = open("D:\\桌面\\stock_prices.csv")
data=pd.read_csv(f)

2.2.3分割数据

# 分割数据
X = data.drop(['Stock_Price'], axis=1)
y = data['Stock_Price']

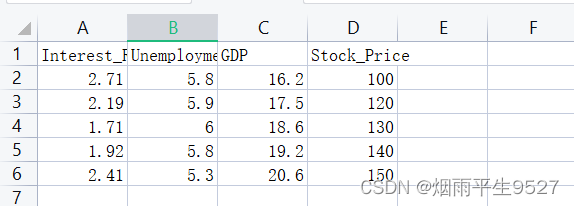
将dataframe中的数据分为自变量和因变量。在这个例子中，自变量包括利率、失业率和GDP，而因变量是股票价格。

2.2.4模型

# 定义模型
model = LinearRegression()

# 训练模型
model.fit(X, y)

使用sklearn.linear_model.LinearRegression构建线性回归模型，并对其进行训练，从而得到一个能够对股票价格进行预测的模型。

2.2.5设定输入参数

problem = {
    'num_vars': 3,
    'names': ['Interest_Rate', 'Unemployment_Rate', 'GDP'],
    'bounds': [[0, 0.1], [0, 0.1], [16, 18]]
}

定义了要进行敏感性分析的自变量及其取值范围

2.2.6生成样本

param_values = saltelli.sample(problem, 1000)

使用SALib.sample.saltelli生成参数的样本，其中problem是参数取值范围和变量名的一个字典，1000是生成的样本数。这里采用的是Sobol采样方法。

2.2.7运行模型

Y = np.zeros([param_values.shape[0]])
for i, X1 in enumerate(param_values):
    Y[i] = model.predict([X1])[0]

使用上面训练好的模型预测每个样本的因变量值，并将结果存储在Y中。

2.2.8分析敏感性

Si = sobol.analyze(problem, Y)

# 输出结果
print(Si['S1'])
print(Si['ST'])

使用SALib.analyze.sobol计算每个自变量的主效应和交互效应，并输出结果。其中，Si['S1']是主效应，表示每个自变量对因变量的贡献程度；Si['ST']是总效应，表示所有自变量的贡献程度

S1：包含每个输入参数的第一类Sobol指数。
ST：包含每个输入参数的总体变化指数。

import matplotlib.pyplot as plt
# 绘制Sobol分析结果的条形图
fig, ax = plt.subplots()
ax.bar(problem['names'], Si['S1'], yerr=Si['S1_conf'])
ax.set_ylabel('S1 sensitivity index')
ax.set_xticklabels(problem['names'])
ax.set_xticks(range(len(problem['names'])))
plt.show()

其中，problem['names']是输入变量名称列表，Si['S1']是每个变量的第一类Sobol指数，Si['S1_conf']是每个指数的置信区间。通过这个函数，我们可以将每个变量的敏感性指数和它的置信区间一起绘制在条形图上。
其中，range(len(problem['names']))生成一个整数列表，用于将输入变量名称列表中的每个名称与x轴上的一个整数刻度线对应。

完整代码

# 导入所需的包和库
import pandas as pd
from sklearn.linear_model import LinearRegression
from SALib.sample import saltelli
from SALib.analyze import sobol
import numpy as np

# 加载数据
f = open("D:\\桌面\\stock_prices.csv")
data=pd.read_csv(f)


# 分割数据
X = data.drop(['Stock_Price'], axis=1)
y = data['Stock_Price']

# 定义模型
model = LinearRegression()

# 训练模型
model.fit(X, y)

# 设定输入参数
problem = {
    'num_vars': 3,
    'names': ['Interest_Rate', 'Unemployment_Rate', 'GDP'],
    'bounds': [[0, 0.1], [0, 0.1], [16, 18]]
}

# 生成样本
param_values = saltelli.sample(problem, 1000)

# 运行模型

Y = np.zeros([param_values.shape[0]])

#label_need=X.keys()[1:]
#X1=X[label_need].values

for i, X1 in enumerate(param_values):
    Y[i] = model.predict([X1])[0]

# 分析敏感性
Si = sobol.analyze(problem, Y)

# 输出结果
print(Si['S1'])
print(Si['ST'])