信号的描述
1.1 连续时间与离散时间信号
一 信号
信号可以描述范围极其广泛的物理现象。信号可以分为确知信号与随机信号，也可以分为连续时间信号与离散时间信号。
确知信号可以表示成一个或几个自变量的函数。

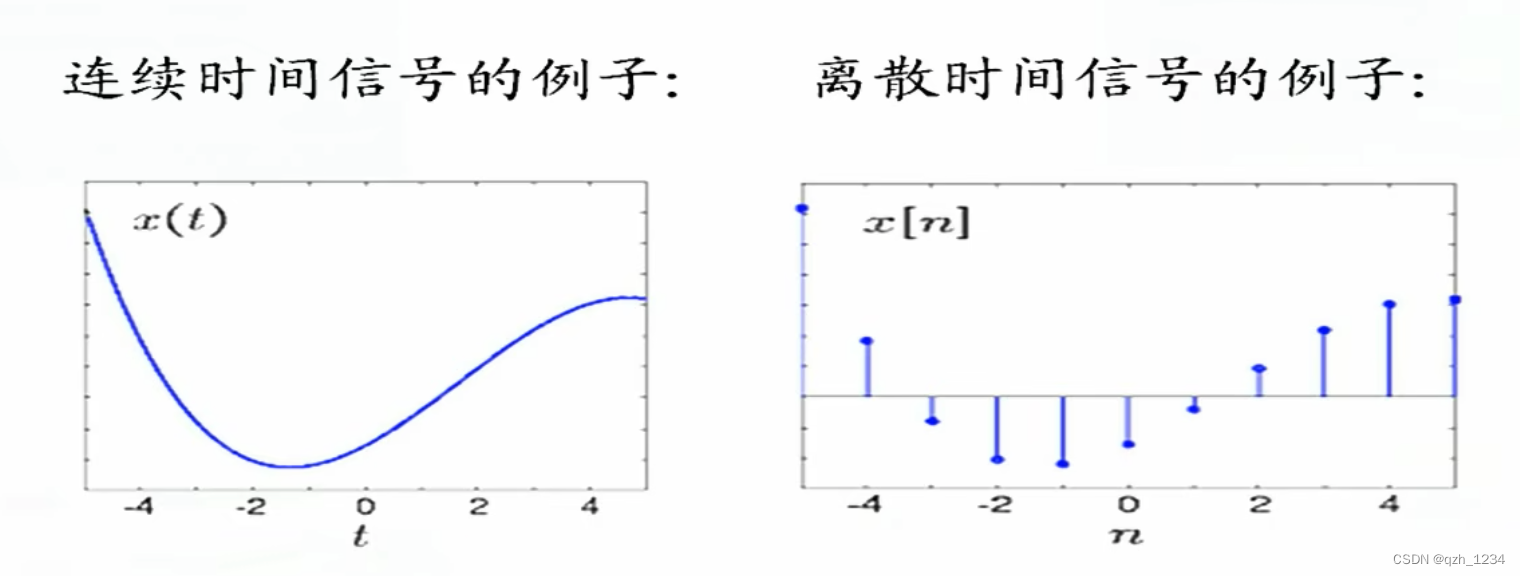
信号的描述
连续时间信号 x(t), x(t₁, t₂)…
离散时间信号 x(n), x(n₁,n₂)…
连续时间信号在离散时刻点上的样本可以构成一个离散时间信号。
二 信号的能量与功率
连续时间信号在[t₁,t₂]区间的能量定义为:
$$E={\int }_{t_1}^{t_2}|x(t){|}^2\mathrm{d}t$$
连续时间信号在[t₁,t₂]区间的平均功率定义:
$$P=\frac{1}{t_2-t_1}{\int }_{t_1}^{t_2}|x(t){|}^2\mathrm{d}t$$
离散时间信号在[n₁,n₂]区间的能量定义为:
$$E=\sum _{n=n_1}^{n_2}|x(n){|}^2$$
离散时间信号在[n₁,n₂]区间的平均功率为:
$$P=\frac{1}{n_2-n_1+1}\sum _{n=n_1}^{n_2}|x(n){|}^2$$
在无限区间上也可以定义信号的总能量:
连续时间情况下:
$$E=\underset{T\to \infty }{\lim }{\int }_{-T}^T|x(t){|}^2\mathrm{d}t={\int }_{-\infty }^{\infty }|x(t){|}^2\mathrm{d}t$$
离散时间情况下:
$$E{}_{\infty }=\underset{N\to \infty }{\lim }\sum _{-N}^N|x(n){|}^2=\sum _{-\infty }^{\infty }|x(n){|}^2$$
在无限区间内的平均功率可定义为:
$$P{}_{\infty }=\underset{T\to \infty }{\lim }\frac{1}{2T}{\int }_{-T}^T|x(t){|}^2\mathrm{d}t$$
$$P{}_{\infty }=\underset{N\to \infty }{\lim }\frac{1}{2N+1}\sum _{-N}^N|x(n){|}^2$$

信号的自变量变换
基本信号
系统及其数学模型
系统的性质