paper: https://arxiv.org/pdf/2009.00225.pdf
code: https://github.com/baoshengyu/H3R
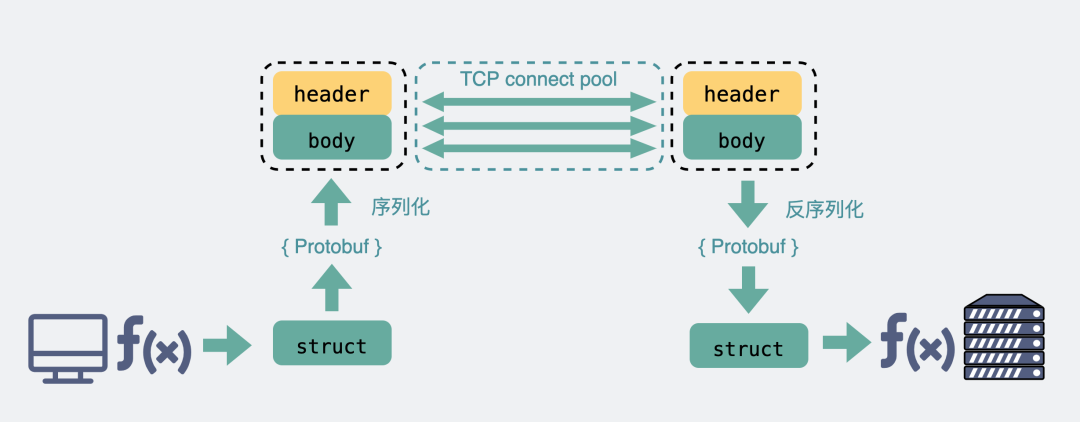
- 总结:本文提出一套编解码方法:
- 编码:random-round整数化 + 激活点响应值表征小数部分,使得GT可以通过编码后的heatmap解码得到;
- 解码:提出两种激活点选择,最终预测值为激活点坐标 * 激活值的加权和。
- WFLW上结果非常好
- 该方法是2021年8月26日挂载arxiv上,早于Local Soft-max(Subpixel Heatmap Regression for Facial Landmark Localization),两篇文章都是想解决热图的量化误差问题,解码思路很相近。
beyond the scope of this paper;
目录
摘要
方法
量化系统
量化误差
激活点的选择
实验
人脸关键点检测编辑
全身位姿检测
消融实验
摘要
- 本文探索了热图回归中的量化误差问题;
- 本文提出了一个简单但有效的系统randomized rounding operation,包含两个部分:
- 在训练时,用一种概率方法,将坐标小数部分编码到GT heatmap中;
- 在测试时,从激活点集合中解码预测坐标
- 本文在人脸关键点数据集(WFLW、300W、COFW和AFLW)和人体位姿检测数据集(MPII和COCO)上实验验证了本文方法的有效性。
方法
- 介绍热图回归中的量化系统;
- 在该系统中公式化描述量化误差;
- 通过随机近似(randomized rounding)设计了新的量化系统。
量化系统
现有方法:1)编码:针对浮点坐标,计算Gaussian kernel matrix开销大,现有方法是将坐标整数化后,使用kernel模型填充;2)解码:最大激活点。
本文从误差出发,将误差拆分为热图误差和量化误差:
其中,x^p是预测值,x_q是GT,x_opt则是自设GT,自设GT是指根据GT坐标编码后的热图,解码得到的坐标值。本文只考虑量化误差。
量化误差
首先定义误差,其中s为放缩倍数,例如原图大小为256,热图为64,则放缩倍数为4。

其次定义坐标整数化,其中t为整数化阈值,对round来说,t=0.5。
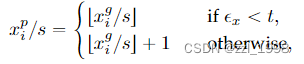
量化偏差(quantization bias)为:

因此,当t=0.5,也即整数化方法是round时,编码方法是无偏的。对于t的其他取值,可以在解码时加入偏移量,使它无偏:
![]()
虽然,上述编码系统是无偏的,但是它会导致non-invertible localization error,也即当整数化后,误差就不可避免了。
定理1:当量化系统是无偏时,量化误差的上限是:![]()
由定理1可知,当s越大,误差也即越大。
Randomized Rounding

本文提出Randomized Rounding,通过多个激活点去表示整数化误差,
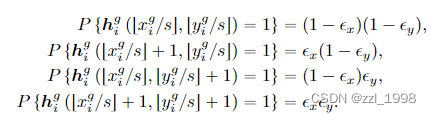
并提出random-round:

希望预测热图为:
![]()
最后的解码为: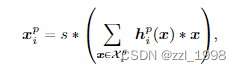
激活点为四个:

定理2:当为上述编解码操作时,量化系统是无偏的,且没有量化误差。
激活点的选择
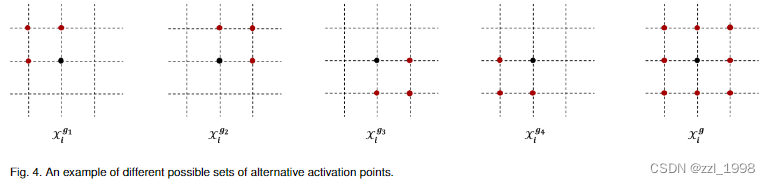
包含两套方案:
1)取得极值点后,包围近邻点都是激活点,例如上图;
2)选择tok p个点,这些点为激活点。
实验
人脸关键点检测

全身位姿检测

消融实验
当使用高斯热图时,sigma越大,需要的激活点越多,最好效果在sigma=1.0/1.5时取得。






![[项目篇] 音乐播放器开发报告](https://img-blog.csdnimg.cn/7315f7f827064fa18a525813d21c9979.png#pic_center)