根据呼文军[1]等建立的购房决策数学模型式(1)[1],通过对影响购房的多个因素进行科学地分析、比较,从若干备选购房方案中做出最佳的选择。
Q=P*WT (1)
在文章的“实例分析”中,假设某位青年教师需要通过决策方案购买房屋,综合该教师所在城市的房源进行筛选,最终选择在A、B、C、D四个小区中做最后的备选方案,确定影响购房的因素有五个:①房屋价格;②房屋面积;③与单位的距离;④房屋设计;⑤房屋周边情况。
房源情况表如下:
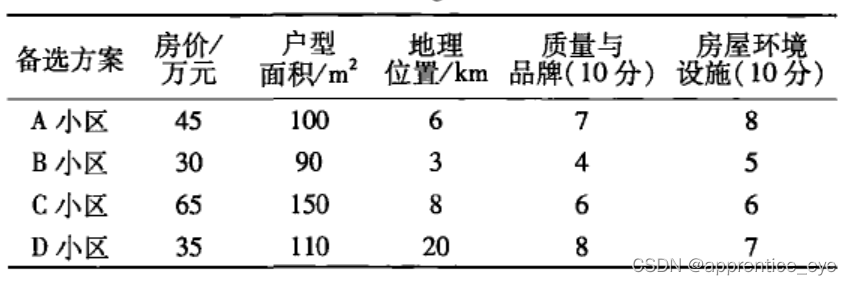
第1步:根据4个小区(备选方案)房源情况建立了评价矩阵B:

第2步:根据第1步建立的评价矩阵求出理想方案,房价和位置为逆向指标,故选最小值为最优值;房屋面积、品牌、环境设施情况为正向指标,故选最大值为最优值,最优值矩阵C为:
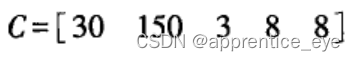
第3步:根据评价矩阵B和的评价矩阵和最优值矩阵C定义建立了同一度矩阵P

P矩阵中各元素为对应评价B矩阵元素除以相应列的最优值(最优质为最大值),或最优值除以对应元素(最优质为最小值)
第4步:根据五种影响购房因素的权重计算出权系矩阵W
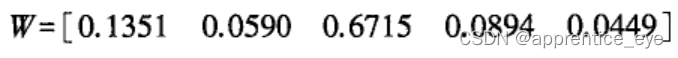
第5步:根据式(1)计算得到4个备选方案与理想方案的接近Q

在Q中越大的值就是越接近理想方案的选择,最大值为0.9148即B小区为最佳备选购房方案。
假设已知房源情况表、权系矩阵W,编程计算找出最佳备选购房方案。
要求输入P、W矩阵数据,计算Q值,在Q中找出最大值对应的备选方案中的小区。(数据处理中保留4位小数)
输入输出示例:
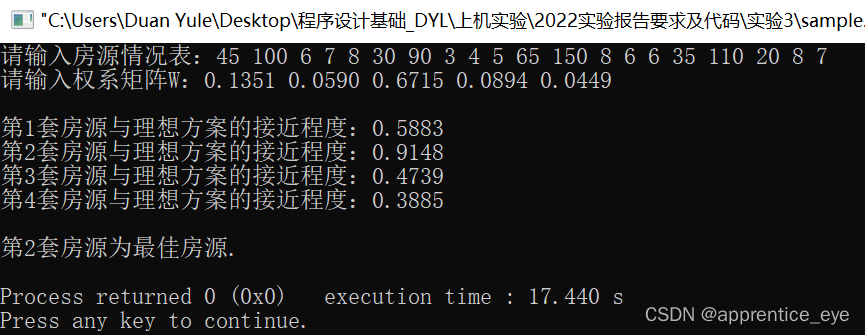
代码实现:
#include<stdio.h>
void ZYZ(float b[][5],float c[]){
for(int i=0;i<4;i++){
for(int j=0;j<5;j++){
if(i==0){
c[j]=b[i][j];
continue;
}
if(j==0||j==2){
if(c[j]>b[i][j]){
c[j]=b[i][j];
}
}else{
if(c[j]<b[i][j]){
c[j]=b[i][j];
}
}
}
}
}
void TYD(float b[][5],float c[],float p[][5]){
for(int i=0;i<4;i++){
for(int j=0;j<5;j++){
if(j==0||j==2){
p[i][j]=c[j]/b[i][j];
}else{
p[i][j]=b[i][j]/c[j];
}
}
}
}
void Q(float p[][5],float w[][1],float q[][1],int *index){
for(int i=0;i<4;i++){
for(int j=0;j<5;j++){
q[i][0]+=p[i][j]*w[j][0];
if(q[*index][0]<q[i][0]){
*index=i+1;
}
}
}
}
int main(){
int index=0;
float b[4][5],c[5],p[4][5],w[5][1],q[5][1];
printf("请输入房源情况表:");
for(int i=0;i<4;i++){
for(int j=0;j<5;j++){
scanf("%f",&b[i][j]);
}
}
printf("请输入权系矩阵W:");
for(int i=0;i<5;i++){
scanf("%f",&w[i][0]);
}
ZYZ(b,c);
TYD(b,c,p);
Q(p,w,q,&index);
printf("\n");
for(int i=0;i<4;i++){
printf("第%d套房源与理想方案接近程度:%.4f\n",i+1,q[i][0]);
}
printf("\n第%d套房源为最佳房源",index);
return 0;
}